複素関数

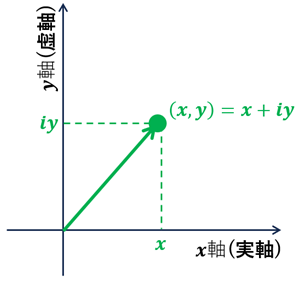
一般に 複素数 は次の形で表される。 \[ z=x+iy\ \] ここで \(i\) は 虚数単位 (\(i^2=-1\)), \(x, y\) は実数

・\(x\) を \(z\) の 実部(実数部分) といい, \(Re(z)\) と記す。
・\(y\) を \(z\) の 虚部(虚数部分) といい, \(Im(z)\) と記す
・複素数全体の集合を \(\mathbb{C}\) で表す

複素数の同値性と四則

\(z_1 = x_1 + iy_1\), \(z_2 = x_2+iy_2\) とすると、複素数の同値性,四則は以下の様に定義される。 \[ \begin{align} &z_1 = z_2 \Longleftrightarrow x_1 = x_2,\; y_1 = y_2 \tag{1} \\ \\ &z_1\pm z_2 =(x_1\pm x_2)+i(y_1\pm y_2) \tag{2} \\ \\ &z_1\cdot z_2 =(x_1x_2 - y_1y_2)+i(x_1y_2+x_2y_1) \tag{3} \\ \\ &\frac{z_2}{z_1} =\frac{x_1x_2+y_1y_2}{x_1^2+y_1^2}+i\frac{x_1y_2-x_2y_1}{x_1^2+y_1^2}　(z_1 \neq 0) \tag{4} \end{align} \] 上の四則の定義により、複素数全体の集合 \(\mathbb{C}\) は体になる。(証明はこちら)。

例題1.1

(1) \((-3+i)(2-5i)\)

(2) \(\displaystyle\frac{3+i}{1-2i}\)

(3) \(\displaystyle\frac{i}{1+i}+\frac{1+i}{i}\)

複素数の絶対値と共役複素数

\(\sqrt{x^2+y^2}\) を複素数 \(z=x+iy\) の絶対値といい、\(|z|\) と記す。

\(z = x+iy\) に対して \(\overline{z}=x-iy\) を \(z\) の共役複素数という。

絶対値、共役複素数について、次の公式が成り立つ。 \[ z+\overline{z}=2Re(z),　z-\overline{z}=2iIm(z) \tag{5} \] \[ \overline{(\overline{z})}=z,　|z|=|\overline{z}|,　z\overline{z}=|z|^2 \tag{6} \] \[ \overline{z_1\pm z_2}=\overline{z}_1\pm \overline{z}_2,　\overline{z_1z_2}=\overline{z}_1\overline{z}_2,　\overline{\left(\frac{z_2}{z_1}\right)}=\frac{\overline{z}_2}{\overline{z}_1}　(z_1\neq 0) \tag{7} \] \[ |z_1z_2|=|z_1||z_2|,　\left|\frac{z_2}{z_1}\right|=\frac{|z_2|}{|z_1|}　(z_1 \neq 0) \tag{8} \] \[ ||z_1|-|z_2|| \leq |z_1\pm z_2| \leq |z_1|+|z_2|　(三角不等式) \tag{9} \] 証明はこちら

複素平面

平面 \(\Pi\) 上に1つの直交座標系を定め, 点\((x,y)\) に複素数 \(z=x+iy\) を対応させて, \(\Pi\) 上の点全体と、複素数全体 \(\mathbb{C}\) との間に 1:1 の対応を与えた場合, この平面 \(\Pi\) を複素平面または, Gauss平面 という。

2つの実数の組 \((x,y)\) の集合は, 加法, スカラー倍によって2次元ベクトル空間になる。
→ 複素数全体の集合 \(\mathbb{C}\) も2次元ベクトル空間と考えることができる。 \[ \begin{array}{l c} (加法) & (x_1,y_1)+(x_2,y_2)=(x_1+x_2, y_1+y_2) \\ & \updownarrow \\ & z_1+z_2 = (x_1+iy_1)+(x_2+iy_2)=(x_1+x_2)+i(y_1+y_2) \\ \\ (スカラー倍) & a(x, y) = (ax, ay) \\ & \updownarrow \\ & a(x+iy) = (ax) + i(ay) \end{array} \]

例題1.2

ⅰ) 複素平面上の直線は、次の形で表されることを示せ。 \[ \overline{\alpha}z+\alpha\overline{z}+c = 0　(\alpha\neq 0, cは実数) \]
ⅱ) 複素平面上の円は、次の形で表されることを示せ。 \[ kz\overline{z}+\overline{\alpha}z+\alpha\overline{z}+c=0　(k\neq 0 および c は実数,\alpha\overline{\alpha}\gt kc) \]
ⅲ) 楕円 \(\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1　(a\gt b\gt 0)\) を \(z,\overline{z}\) を用いて表せ。

例題1.3

ⅰ) 複素平面上の 3 点 \(z_1,z_2,z_3\) を頂点とする三角形 \(\triangle z_1z_2z_3\) の重心を表す点は \(\frac{1}{3}(z_1+z_2+z_3)\) であることを示せ。

ⅱ) \(|z_1-z_2|^2+|z_1+z_2|^2=2(|z_1|^2+|z_2|^2)\) を証明せよ。(三角形の中線定理)

ⅲ) \(z=x+iy　(y\neq 0)\) のとき, \(z^3\) が実数となるための条件を求めよ。

極形式

平面上の点 \((x,y)\) を表すのに極座標を使って \[ \begin{align} x &= r\cos(\theta) \\ y &= r\sin(\theta) \end{align} \] と表すことができる。複素数も同様に \[ z=r(\cos(\theta)+i\sin(\theta)) \] と表すことができる。これを \(z\) の極形式という。

・\(r=|z|\geq 0\)
・\(\theta\) を \(z\) の偏角といい, \(arg\; z\) で表す。
・\(r=0\) の場合, \(arg\;z\) は定義しない。
・\(r\gt 0\) のとき、\((r,\theta+2n\pi)\;(n=0,\pm1,\pm2,...)\) は同一の \(z\) に対応する。
・\(z\) の偏角のうち, \(-\pi\lt arg\;z\leq \pi\) を満足するものを偏角の主値といい, \(Arg\;z\) と記す。

\(z_1=r_1(\cos(\theta_1)+i\sin(\theta_1)), z_2=r_2(\cos(\theta_2)+i\sin(\theta_2))\) のとき \[ \begin{align} z_1z_2 &= r_1r_2\{\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)\} \tag{12} \\ \\ \frac{z_2}{z_1} &= \frac{r_2}{r_1}\{\cos(\theta_2-\theta_1)+i\sin(\theta_2-\theta_1)\}\;(z_1\neq 0) \tag{13} \end{align} \]

証明はこちら。

公式(12)を繰り返し使えば, de Moivreの定理と呼ばれる次の公式が得られる。

\[ z=r\{\cos(\theta)+i\sin(\theta)\} \Rightarrow z^n=r^n\{\cos(n\theta)+i\sin(n\theta)\}\;(n:整数) \tag{14} \]

例題1.4

・\(z^n=a\;(a\neq 0)\) を解け。ただし \(n\) は正の整数とする。

・1 の \(n\) 乗根を求め, 複素平面上に図示せよ。

解答はこちら。

例題1.5

\(\theta\) が \(2\pi\) の整数倍でないとき, 次の等式を証明せよ。 \[ \begin{align} &1+\cos(\theta)+\cos(2\theta)+\cdots+\cos(n\theta) = \cos\left(\frac{n\theta}{2}\right)\sin\left(\frac{(n+1)\theta}{2}\right)\Big/\sin\left(\frac{\theta}{2}\right) \\ \\ &\sin(\theta)+\sin(2\theta)+\cdots+\sin(n\theta)=\sin\left(\frac{n\theta}{2}\right)\sin\left(\frac{(n+1)\theta}{2}\right)\Big/\sin\left(\frac{\theta}{2}\right) \end{align} \] 証明はこちら。

直線の長さと 2 直線のなす角

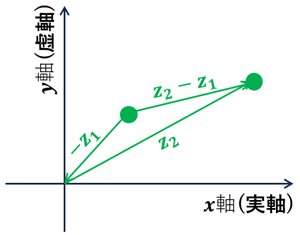
2点 \(z_1,z_2\) が与えられたとき
・\(z_1\)を始点, \(z_2\) を終点とするベクトルは複素数 \(z_2-z_1\) によって表される。
・その長さは \(|z_2-z_1|\) で表される

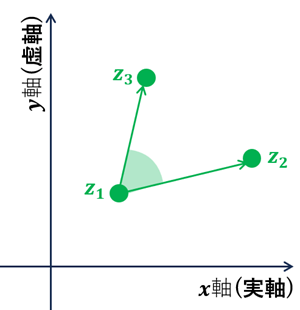
3点 \(z_1,z_2,z_3\) が与えられたとき
・2つのベクトル \(z_2-z_1\) と \(z_3-z_1\) のなす角は
　\(\angle z_2z_1z_3 = \left|Arg\left(\displaystyle\frac{z_3-z_1}{z_2-z_1}\right)\right|\)

例題1.6

・\(z_1,z_2,z_3\) が正三角形をなす条件は \[ z_1^2+z_2^2+z_3^2-z_2z_3-z_3z_1-z_1z_2=0 \] 　であることを証明せよ。

・\(z_1\cdot z_2,　\displaystyle\frac{z_2}{z_1}\; (z_1\neq 0)\) を複素平面上で作図せよ。

証明はこちら。

複素平面 \(\mathbb{C}\) における点集合の性質

　※集合に何らかの数学的構造 (四則, スカラー倍, 絶対値, 距離など)を加味した場合
　　集合　　　　\(\Rightarrow\) 空間と呼ばれる
　　集合の要素　\(\Rightarrow\) 点とよばれる

・複素数には絶対値が定義されている (ノルム空間)
・2点の複素数の差も複素数になる (複素数は体)
・2点の複素数の差も絶対値を持つ (距離空間)
\(\Rightarrow\) 点と点の距離に関連した性質を論ずることができる。

距離

・複素平面上の2点 \(z_1=x_1+iy_1, z_2=x_2+iy_2\) に対し,
\(|z_1-z_2|=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\) が \(z_1,z_2\) の距離である。

有界

・集合 \(D\) の任意の点 \(z\) に対し, \(|z|\leq K\) である定数 \(K\) が存在するとき, 集合 \(D\) は有界であるという。

近傍・内点・外点・境界点

・点 \(z_0\) を中心とした半径 \(\varepsilon \gt 0\) の円の内部, すなわち集合 \(U_\varepsilon(z_0)=\{z\mid |z-z_0|\lt \varepsilon\}\) を \(z_0\) の ε近傍 という。いろいろなεに対する \(z_0\) のε近傍を総称して \(z_0\) の近傍という。

・集合 \(D\) に属する点 \(z_0\) が \(D\) に含まれる \(z_0\) のある近傍をもつとき, \(z_0\) を \(D\) の内点という。

・点 \(z_1\) のある近傍が \(D\) の点を1つも含まないとき, \(z_1\) を \(D\) の外点という。

・\(D\) の内点でも外点でもない点, すなわち, \(z_2\) のどんな近傍も \(D\) に属する点と属さない点が存在するとき, \(z_2\) を \(D\) の 境界点 といい, \(D\) の境界点全体を \(D\) の境界という。

集積点・孤立点

・点 \(z_0\) のどんな近傍にも \(D\) の点が無数に含まれているとき, \(z_0\) を \(D\) の 集積点 という。

・\(D\) の点で \(D\) の集積点でないもの, すなわち, \(D\) の点 \(z_1\) で, \(z_1\) のある近傍が \(z_1\) 以外に \(D\) の点を含まないとき, \(z_1\) を \(D\) の 孤立点 という。

開集合・閉集合

・内点のみからなる集合を 開集合 という。

・ある集合がその集積点をすべて含んでいるとき, その集合を 閉集合 という。

・問
　ある集合に属さない点全体の集合をその集合の補集合という。開集合の補集合は閉集合であり、閉集合の補集合は開集合であることを示せ。

解答はこちら。

連結・閉領域

・集合 \(D\) に属する任意の2点を \(D\) 内の連続曲線で結べるとき, \(D\) は連結であるといい, 連結な開集合を領域という。

・領域にその境界点をつけ加えてえられる集合を 閉領域 という。

例題 1.7

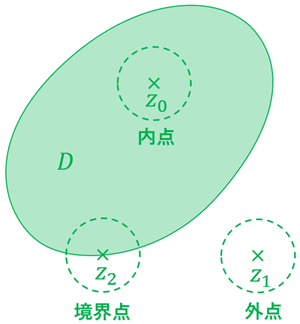
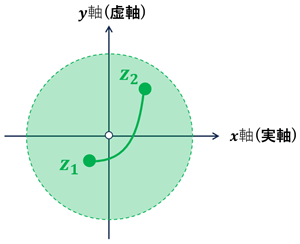
・\(\{z\mid 0\lt |z|\lt 1\}\) は領域である。

　境界を含まないので開集合
　任意の2点を原点を通らないようにして集合内の点で結ぶことができるので連結
　たとえば
　 - 大きさ：\(|z_1|\rightarrow |z_2|\)
　 - 偏角：\(Arg(z_1)\rightarrow Arg(z_2)\)
　を補間して結ぶことができる。

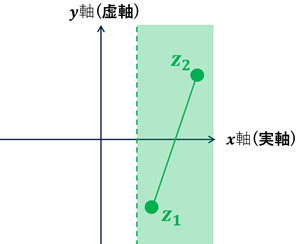
・\(\{z\mid 1\lt Re(z)\}\) は領域である。

　境界を含まないので開集合
　任意の2点は集合内の点で直線で結ぶことができるので連結

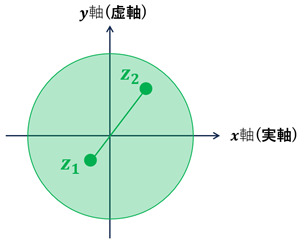
・\(\{z\mid |z|\leq 1\}\) は閉領域である。

　境界を含むので閉集合
　任意の2点は集合内の点で直線で結ぶことができるので連結

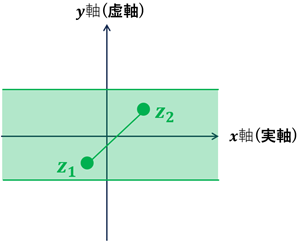
・\(\{z\mid |Im(z)|\leq 1\}\) は閉領域である。

　境界を含むので閉集合
　任意の2点は集合内の点で直線で結ぶことができるので連結

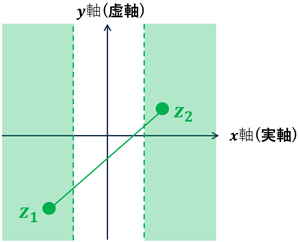
・\(\{z\mid 1\lt |Re(z)|\}\) は開集合であるが, 領域ではない。

　境界を含まないので開集合
　任意の2点は集合内の点で結ぶことができない場合があるので連結ではない

例題 1.8

・複素平面から負の実軸および原点を除いてできる領域
　\(\{z\mid z+|z|\neq 0\}\) と表すことができる。

1. 複素平面

1.1 複素平面

複素数の定義