●\(z_1,z_2,z_3\) が正三角形をなす条件は
\[
z_1^2+z_2^2+z_3^2-z_2z_3-z_3z_1-z_1z_2=0
\]
であることを証明せよ。
(解答)
・\(z_1,z_2,z_3\) が正三角形をなす条件は
\[
|z_2-z_1|=|z_3-z_1|, \angle z_2z_1z_3 = \frac{\pi}{3}
\]
\[
\therefore \left|\frac{z_3 - z_1}{z_2-z_1}\right|=1, Arg\left(\frac{z_3-z_1}{z_2-z_1}\right)=\pm\frac{\pi}{3}
\]
これは大きさが 1 で偏角が \(\pm\displaystyle\frac{\pi}{3}(=\pm 60^\circ)\) の複素数なので
\[
\therefore \frac{z_3-z_2}{z_2-z_1}=\cos\frac{\pi}{3}\pm i\sin\frac{\pi}{3}
\]
右辺は -1 の3乗根で \(z^2-z+1=0\) の根。
(\(z^3=-1 \Rightarrow z^3+1=0 \Rightarrow (z+1)(z^2-z+1)=0\))
\[
\begin{align}
&\therefore \left(\frac{z_3-z_1}{z_2-z_1}\right)^2-\left(\frac{z_3-z_1}{z_2-z_1}\right)+1 = 0 \\
\\
&(z_3-z_1)^2 - (z_2-z_1)(z_3-z_1)+(z_2-z_1)^2 = 0 \\
\\
&(z_3^2-\cancel{2}z_3z_1+z_1^2)-(z_2z_3-\cancel{z_2z_1}-\cancel{z_1z_3}+\cancel{z_1^2})+(z_2^2-\cancel{2}z_2z_1+\cancel{z_1^2}) = 0 \\
\\
&z_1^2+z_2^2+z_3^2-z_2z_3-z_3z_1-z_1z_2 = 0
\end{align}
\]
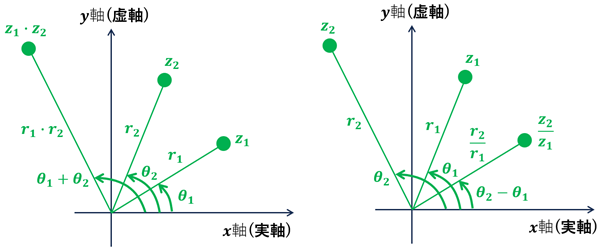
●\(z_1\cdot z_2, \displaystyle\frac{z_2}{z_1}\; (z_1\neq 0)\) を複素平面上で作図せよ。
