\(z^n=a\;(a\neq 0)\) を解け。ただし \(n\) は正の整数とする。
(解答)
・\(a=\rho(\cos(\varphi)+i\sin(\varphi)), z=r(\cos(\theta)+i\sin(\theta))\) とおく
\(r^n(\cos(n\theta)+i\sin(n\theta))=\rho(\cos(\varphi)+i\sin(\varphi))\)
\(\therefore r^n = \rho, n\theta = \varphi+2k\pi(kは整数)\)
\(\therefore r=\sqrt[n]{\rho}, \theta=\frac{\varphi+2k\pi}{n} (k=0,\pm 1,\pm 2,\cdots)\)
\(\therefore z=\sqrt[n]{\rho}\left(\cos\left(\frac{\varphi+2k\pi}{n}\right)+i\sin\left(\frac{\varphi+2k\pi}{n}\right)\right)\)
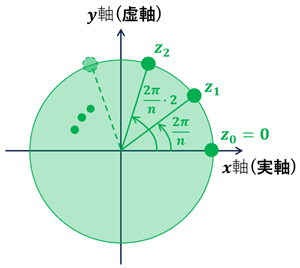
1 の \(n\) 乗根を求め, 複素平面上に図示せよ。
(解答)