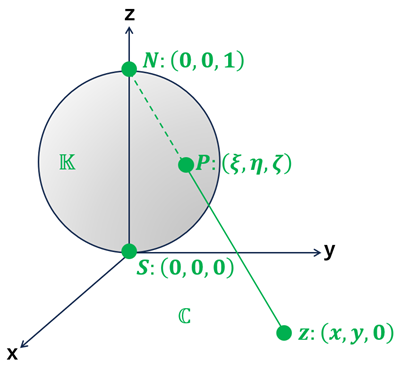

\(\mathbb{K}\) を地球にみたて, \(S\) を南極, \(N\) を北極とすると
・赤道 → \(\mathbb{C}\) の単位円
・南半球 → 単位円の内部
・北半球 → 単位円の外部
に対応する。
\(SN\) を \(z\) 軸にとり, \(P\) の座標を \((\xi,\eta,\zeta)\) とすると
\[
\xi^2+\eta^2+\zeta^2-\zeta=0, \frac{x}{\xi}=\frac{y}{\eta}=\frac{1}{1-\zeta}
\]
(式の導出はこちら)
・\(P\) → \(z\) の関係
(上式の分母を払ったり, 移項したりするだけで得られる)
\[ \begin{align} &x=\frac{\xi}{1-\zeta} \\ \\ &y=\frac{\eta}{1-\zeta} \\ \\ &\xi^2+\eta^2+\zeta^2=\zeta \end{align} \tag{1} \]
となる。
・\(z\) → \(P\) の関係
\[ \begin{align} &\xi=\frac{x}{x^2+y^2+1}=\frac{1}{2}\frac{z+\overline{z}}{z\overline{z}+1} \\ \\ &\eta=\frac{y}{x^2+y^2+1}=\frac{1}{2i}\frac{z-\overline{z}}{z\overline{z}+1} \\ \\ &\zeta=\frac{x^2+y^2}{x^2+y^2+1}=\frac{z\overline{z}}{z\overline{z}+1} \end{align} \tag{2} \]
(式の導出はこちら)
という関係がある。
\(z\) が 原点 \(O\) から遠ざかるに従って, \(P\) は \(N\) に近づく。
原点から無限の距離にある仮想の 1 点を考え, これを 無限遠点 と名づけ, \(\infty\) と記す。
\(\mathbb{C}\) に \(\infty\) を付け加えた \(\overline{\mathbb{C}}\) と \(\mathbb{K}\) の間に 1:1 の対応を付けることができる。
\(\mathbb{K}\) 上の点が複素数および \(\infty\) を表すと考えたとき, \(\mathbb{K}\) を 複素球面 または Riemann球面 という。
\(\overline{\mathbb{C}}\) を広義の複素平面, \(\mathbb{C}\) を 有限複素平面, \(\mathbb{C}\) の元を 有限複素数 と呼ぶことがある。
\(\infty\) と有限複素数 \(\alpha\) に対し
\[
\alpha \pm \infty = \infty \pm \alpha = \infty, \alpha/\infty=0, |\infty|=\infty, \infty\cdot\infty=\infty
\]
\[
\infty/\alpha=\infty, \alpha\cdot\infty=\infty\;(\alpha\neq 0)
\]
と規約する。
複素平面上の次の各点ha, 立体射影によってリーマン球面上のどのような点にうつされるか?
ⅰ) \(1\), ⅱ) \(i\), ⅲ) \(1-2i\)
解答はこちら。
立体射影により \(\mathbb{C}\) 上の円または直線は, \(\mathbb{K}\) 上の円に対応することを示せ。(円円対応)
※ 直線は半径 \(\infty\) の円と見なしてこの事実を円円対応という。
解答はこちら。
次の ⅰ), ⅱ) の \(\mathbb{C}\) 上への像を求めよ。
ⅰ) \(\mathbb{K}\) の中心に対して対称な2点
ⅱ) \(N\)を通る大円
※球面上の円に沿って球を切断した場合、切断面に球の中心を含む場合, その球面上の円を大円という。
(球面上の 2 点は大円に沿った経路が最短になる → 球面上の直線のようなもの)
解答はこちら。
\(R\gt 0\) のとき. \(\{z\mid |z|\gt R\}\) と \(\infty\) との合併集合を \(\infty\) の \(R\) 近傍 といい, \(U_R(\infty)\) と記す。
\(R\) のいろいろな値に対する近傍を総称して \(\infty\) の 近傍 と呼ぶ。
\(\mathbb{C}\) 上の数列 \(\{z_k\}\) があるとき, 任意の \(R\gt 0\) に対し, 適当な \(n_0\) が存在して
\[
n\geq n_0 \Rightarrow z_n \in U_R(\infty)
\]
であれば, 数列 \(\{z_k\}\) は \(\infty\) に発散するといい, \(\lim\limits_{n\rightarrow\infty} z_n=\infty\) と記す。
\(\mathbb{C}\) 上の数列 \(\{z_k\}\) に対し, \(\lim\limits_{n\rightarrow\infty}|z_n|=\infty\) と \(\lim\limits_{n\rightarrow\infty}z_n=\infty\) は同値であり, \(z_n\neq 0\) のときはさらに \(\displaystyle\lim\limits_{n\rightarrow\infty}\frac{1}{|z_n|}=0\) とも同値であることを示せ。
解答はこちら。