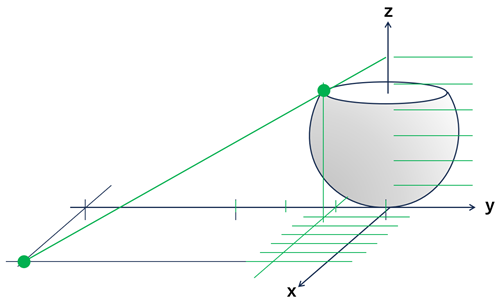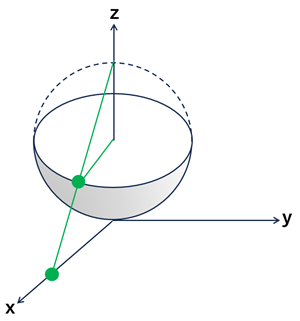
複素平面上の次の各点ha, 立体射影によってリーマン球面上のどのような点にうつされるか?
ⅰ) \(1\), ⅱ) \(i\), ⅲ) \(1-2i\)
公式(2)に \(x,y\) を代入して \(\xi,\eta,\zeta\) を求める。
ⅰ) \(1\)
\[
\begin{align}
&\xi=\frac{x}{x^2+y~2+1}=\frac{1}{1^2+0^2+1}=\frac{1}{2} \\
\\
&\eta=\frac{y}{x^2+y^2+1}=\frac{0}{1^2+0^2+1}=0 \\
\\
&\zeta=\frac{x^2+y^2}{x^2+y^2+1}=\frac{1^2+0^2}{1^2+0^2+1}=\frac{1}{2}
\end{align}
\]

ⅱ) \(i\) \[ \begin{align} &\xi=\frac{x}{x^2+y~2+1}=\frac{0}{0^2+1^2+1}=0 \\ \\ &\eta=\frac{y}{x^2+y^2+1}=\frac{1}{0^2+1^2+1}=\frac{1}{2} \\ \\ &\zeta=\frac{x^2+y^2}{x^2+y^2+1}=\frac{0^2+1^2}{0^2+1^2+1}=\frac{1}{2} \end{align} \]
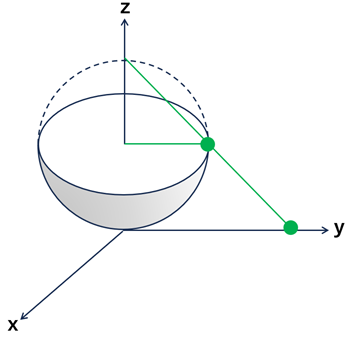
ⅲ) \(1-2i\) \[ \begin{align} &\xi=\frac{x}{x^2+y~2+1}=\frac{1}{1^2+(-2)^2+1}=\frac{1}{6} \\ \\ &\eta=\frac{y}{x^2+y^2+1}=\frac{-2}{1^2+(-2)^2+1}=\frac{-2}{6}=-\frac{1}{3} \\ \\ &\zeta=\frac{x^2+y^2}{x^2+y^2+1}=\frac{1^2+(-2)^2}{1^2+(-2)^2+1}=\frac{5}{6} \end{align} \]