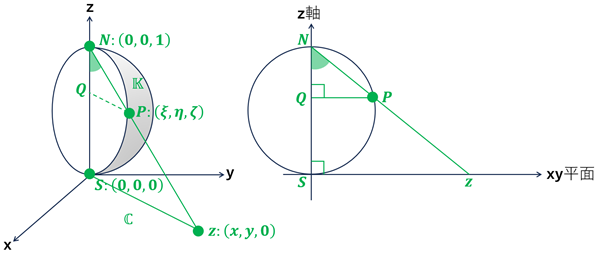
・\(z\) → \(P\) の関係 \[ \begin{align} &\xi=\frac{x}{x^2+y^2+1}=\frac{1}{2}\frac{z+\overline{z}}{z\overline{z}+1} \\ \\ &\eta=\frac{y}{x^2+y^2+1}=\frac{1}{2i}\frac{z-\overline{z}}{z\overline{z}+1} \\ \\ &\zeta=\frac{x^2+y^2}{x^2+y^2+1}=\frac{z\overline{z}}{z\overline{z}+1} \end{align} \] となることを示す。
(式の導出)\(S,N,P\) の作る平面で切断した切断面を考える。

\(\triangle NSz\) と \(\triangle NQP\) は相似なので、\(x,y\) に相似比を掛けて \(\xi,\eta, \zeta\) を求めたいが、
相似比に \(\zeta\) が残ってしまう。
\[
\begin{align}
相似比 &=\frac{\overline{NP}の長さ}{\overline{Nz}の長さ}=\frac{\sqrt{(\xi-0)^2+(\eta-0)^2+(\zeta-1)^2}}{\sqrt{(x-0)^2+(y-0)^2+(0-1)^2}} \\
\\
&=\frac{\sqrt{\xi^2+\eta^2+\zeta^2-2\zeta+1}}{\sqrt{x^2+y^2+1}}\underbrace{=}_{\xi^2+\eta^2+\zeta^2-\zeta=0}\frac{\sqrt{1-\zeta}}{\sqrt{x^2+y^2+1}}
\end{align}
\]
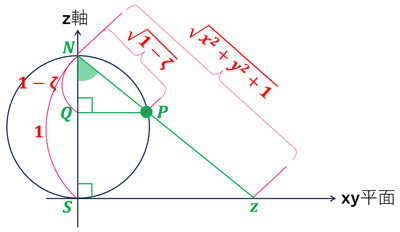
・点 \(P\) の高さが \(\zeta\) で決まるという条件しか使っていないため。
・点 \(P\) が球面上にあるという条件を追加する必要がある。
ピンクの補助線を追加して、もう一個の相似三角形を使って相似比の \(\zeta\) 依存を消す。
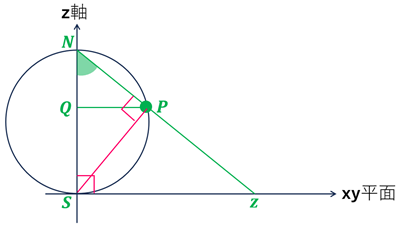
\(NS\) は円の中心を通る直線なので, \(\angle NPS\) は \(90^\circ\) になる。(円周角=中心角÷2, 中心角=180°)
\(\Rightarrow \triangle NSz\) と \(\triangle NPS\) は相似になる。
\[
\begin{align}
&\frac{PN}{NS}=\frac{NS}{zN} \Rightarrow PN=\frac{NS^2}{zN} \\
\\
&\frac{PQ}{zS}=\frac{PN}{zN}\underbrace{=}_{上式を代入}\frac{NS^2}{zN^2}=\frac{1^2}{\sqrt{x^2+y^2+1}^2}=\frac{1}{x^2+y^2+1}
\end{align}
\]
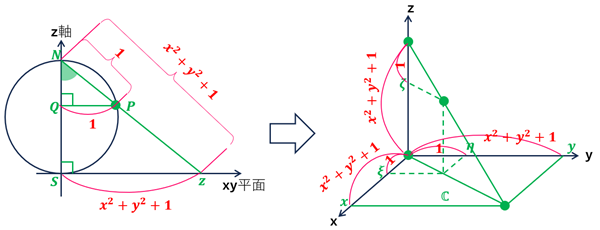
\[ \begin{align} \xi &= \frac{1}{x^2+y^2+1}\cdot x \\ \\ \eta &= \frac{1}{x^2+y^2+1}\cdot y \\ \\ 1-\zeta &= \frac{1}{x^2+y^2+1}\cdot 1 \\ \\ \zeta & = 1 - \frac{1}{x^2+y^2+1}=\frac{x^2+y^2}{x^2+y^2+1} \end{align} \] ここで点 \(z\) を 三次元内の平面上の点表現 (x,y,0) から,複素数表現 \(z=x+iy\) に変えると \[ x=\frac{z+\overline{z}}{2}, y=\frac{z-\overline{z}}{2i}, x^2+y^2=z\overline{z} \] だった。これらを使って \(\xi,\eta,\zeta\) を表現すると \[ \begin{align} \xi &= \frac{x}{x^2+y^2+1} = \frac{1}{2}\frac{z+\overline{z}}{z\overline{z}+1} \\ \\ \eta &= \frac{y}{x^2+y^2+1} = \frac{1}{2i}\frac{z-\overline{z}}{z\overline{z}+1} \\ \\ \zeta & = \frac{x^2+y^2}{x^2+y^2+1} = \frac{z\overline{z}}{z\overline{z}+1} \end{align} \] となる。