次の ⅰ), ⅱ) の \(\mathbb{C}\) 上への像を求めよ。
ⅰ) \(\mathbb{K}\) の中心に対して対称な2点
ⅱ) \(N\)を通る大円
※球面上の円に沿って球を切断した場合、切断面に球の中心を含む場合, その球面上の円を大円という。
(球面上の 2 点は大円に沿った経路が最短になる → 球面上の直線のようなもの)
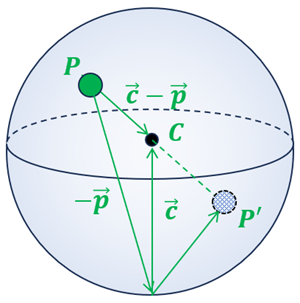
\(\mathbb{K}\)上の点 \(P:(\xi, \eta, \zeta)\)
\(\mathbb{K}\) の中心 \(C: (0,0,0.5)\)
\(PのCに対して対称な点 P'\)
\[
\vec{p}^\prime = \vec{c}+(\vec{c}-\vec{p})=2\vec{c}-\vec{p}
=2
\begin{pmatrix}
0 \\
0 \\
0.5
\end{pmatrix}
-
\begin{pmatrix}
\xi \\
\eta \\
\zeta
\end{pmatrix}
=
\begin{pmatrix}
-\xi \\
-\eta \\
1-\zeta
\end{pmatrix}
\]

または
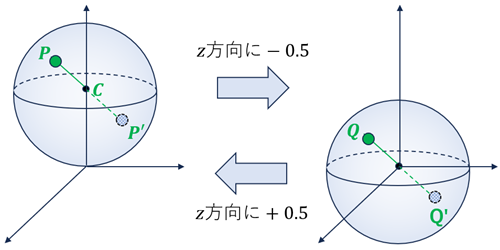
\[ \begin{align} &P=(\xi,\eta,\zeta)をz方向に-0.5 \Longrightarrow Q=(\xi,\eta,\zeta-0.5)\\ \\ &Q の対称点 Q^\prime=(-\xi,-\eta,-\zeta+0.5)\; ・・・\; Q の各座標の正負を反転 \\ \\ &Qの対称点をz方向に+0.5 \Longrightarrow P^\prime=(-\xi,-\eta,-\zeta+1) \end{align} \] 公式(1)より \[ \begin{align} \begin{pmatrix} \xi \\ \eta \\ \zeta \end{pmatrix} \Longrightarrow \begin{pmatrix} \displaystyle\frac{\xi}{1-\zeta} \\ \displaystyle\frac{\eta}{1-\zeta} \end{pmatrix} \\ \\ \begin{pmatrix} -\xi \\ -\eta \\ -\zeta+1 \end{pmatrix} \Longrightarrow \begin{pmatrix} \displaystyle\frac{-\xi}{1-(-\zeta+1)} \\ \displaystyle\frac{-\eta}{1-(-\zeta+1)} \end{pmatrix} = \begin{pmatrix} \displaystyle\frac{-\xi}{\zeta} \\ \displaystyle\frac{-\eta}{\zeta} \end{pmatrix} \end{align} \]
ⅱ)\(N\)を通る大円は, 法線が \((\cos\theta,\sin\theta,0)\) の平面と, \(\mathbb{K}\) との交線になる。
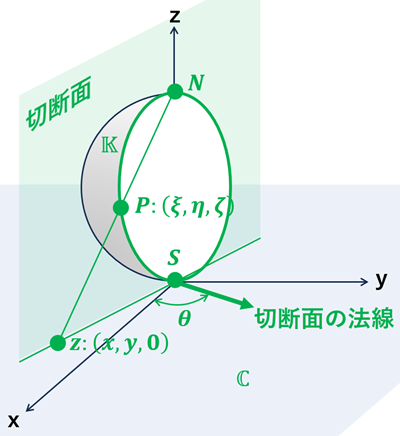
・切断面:法線が \((\cos(\theta),\sin(\theta),0)\) の平面 ・・・ \(x\cos(\theta)+y\sin(\theta)=0,\; z:任意\)
(点 \(N=(0,0,1), 中心=(0,0,0.5), S=(0,0,0)\) は切断面の方程式を満たす。
⇒ 点 \(N\), 中心, 点\(S\) は切断面上にある。
⇒ 切断面は大円 ・・・ 念のため確認)
・大円上の(\(N\) 以外の)任意の点 \(P\) の立体射影 \(z\) も切断面上にある。
(線分 \(\overline{NP}\) の延長線上に \(z\) は存在するので)
⇒ 点 \(P\) の像は切断面と \(z=0\) 平面の交線: \(x\cos(\theta)+y\sin(\theta)=0,\;z=0\) となる。