\(|\sin|\leq 1?,　 |\cos| \leq 1?\)

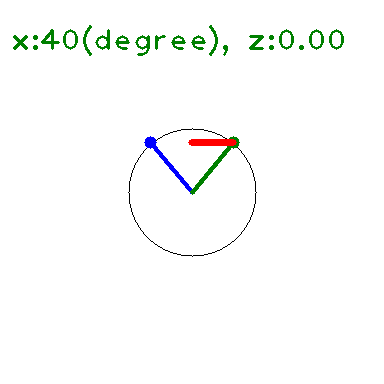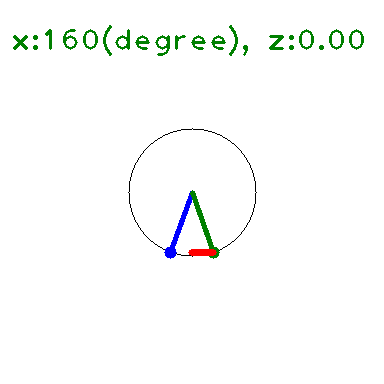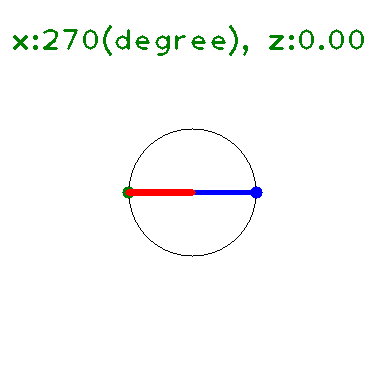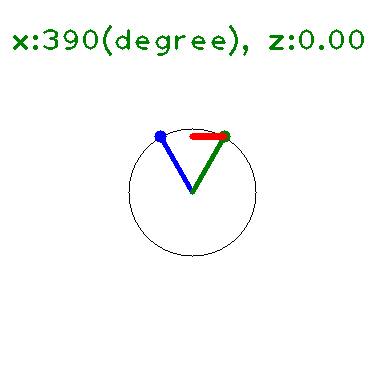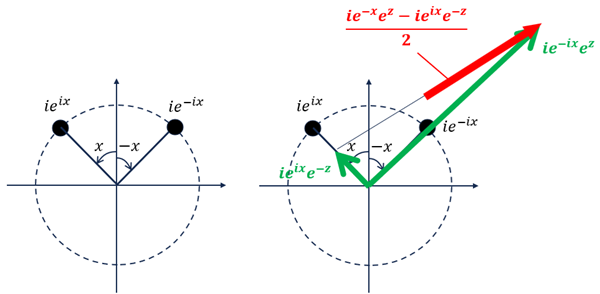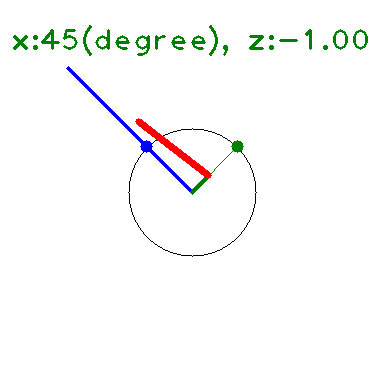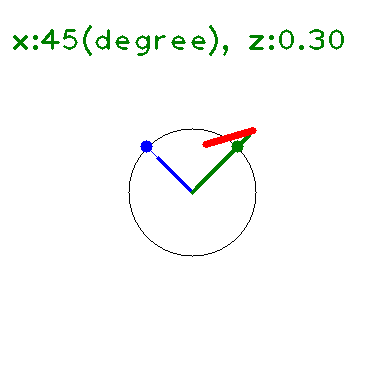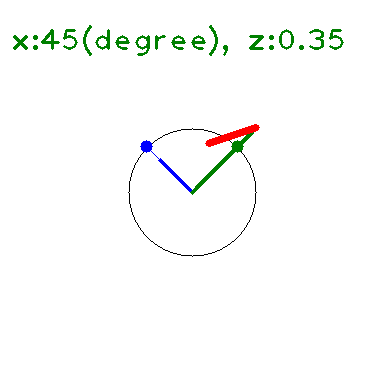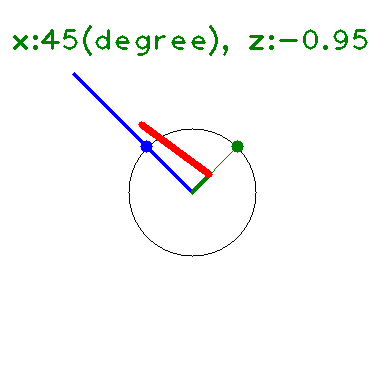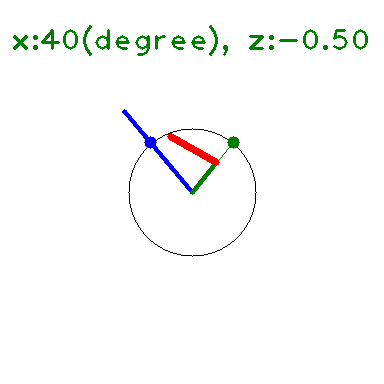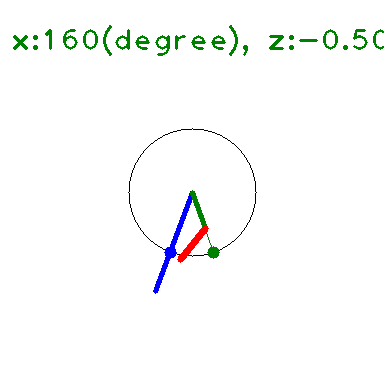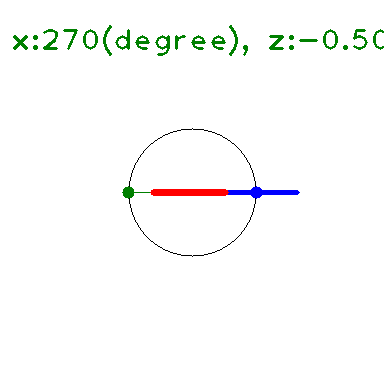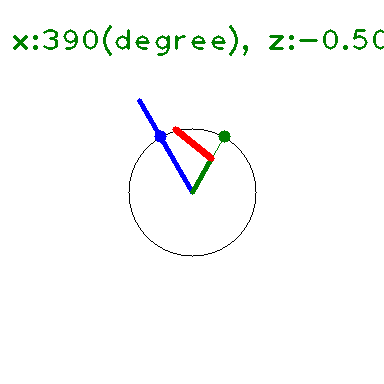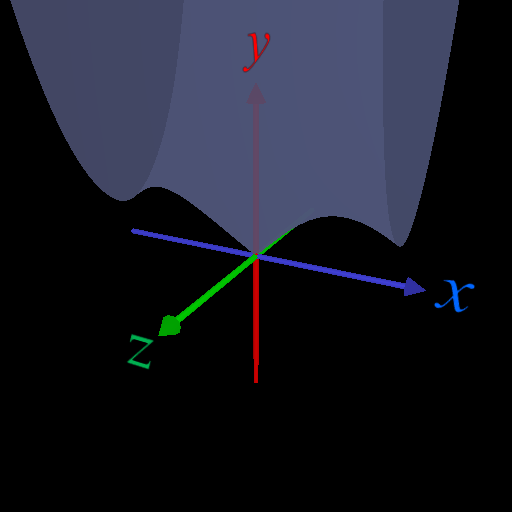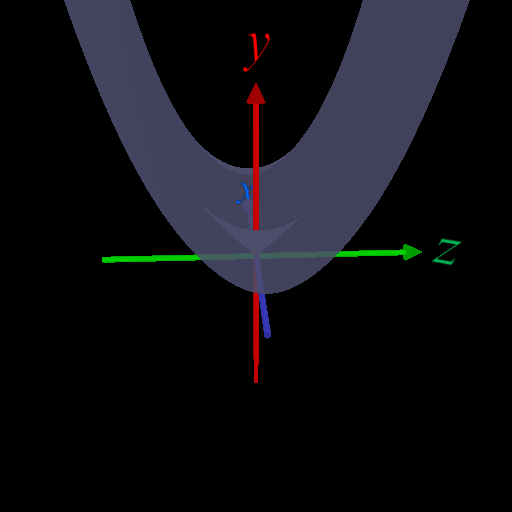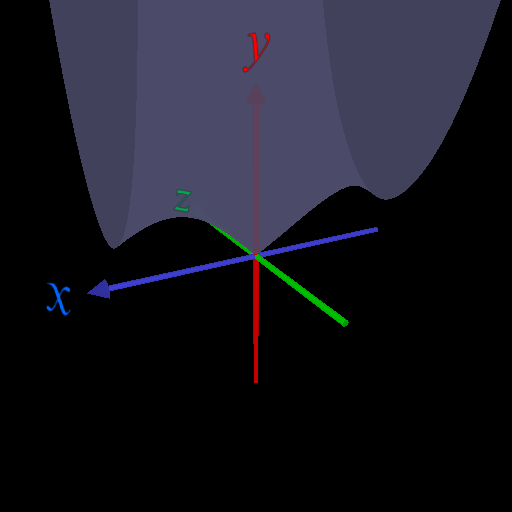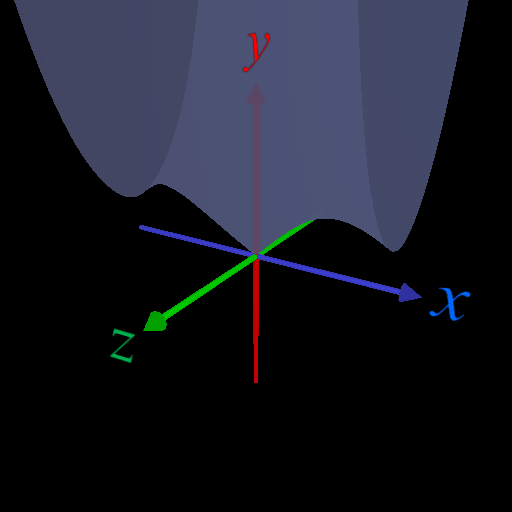
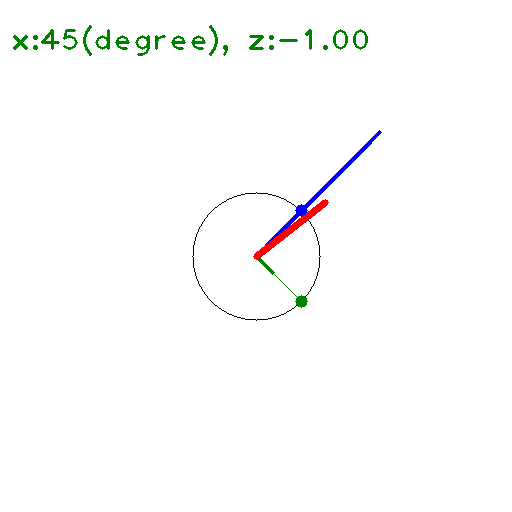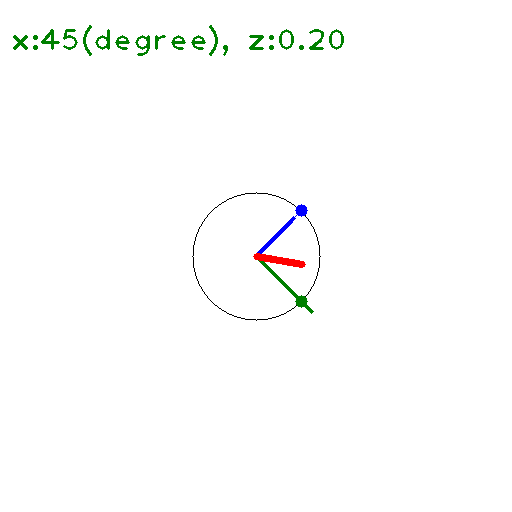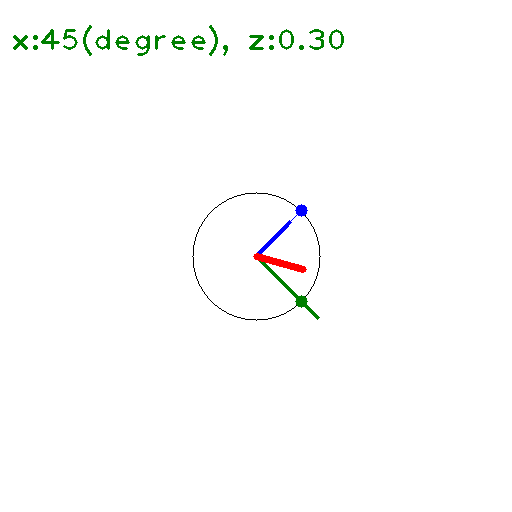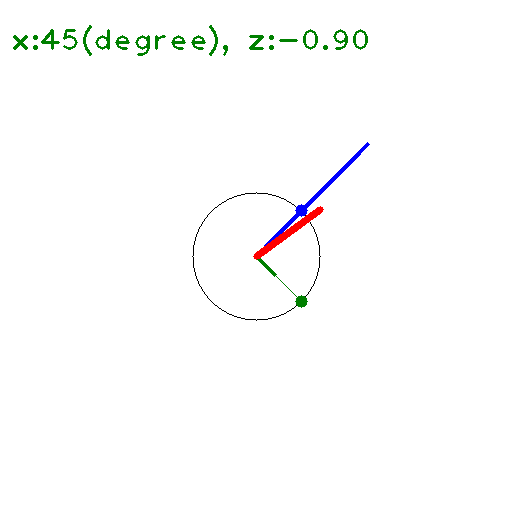
定義域, 値域を複素数に広げると、\(|\sin|\leq 1,|\cos|\leq 1\) は成り立たない。 \[ \cos y = \frac{e^{iy}+e^{-iy}}{2},　 \sin y = \frac{e^{iy}-e^{-iy}}{2i} \] の \(y\) に \(x+iz\) を代入して 大きさを求めると下図のようになる(たぶん)。

\(y = |\sin(x+iz)|\)

\(x\) 軸上(\(z=0\)) では \(\leq 1\) となっている。

計算してみるか･･･ \[ \begin{align} \sin(x+iz) &= \frac{e^{i(x+iz)}-e^{-i(x+iz)}}{2i} 　(定義式に x+iz を代入)\\ \\ &= \frac{e^{ix}e^{-z}-e^{-ix}e^{z}}{2i}　　\left(\leftarrow \frac{i}{i}を掛ける\right) \\ \\ &= \frac{ie^{ix}e^{-z}-ie^{-ix}e^{z}}{-2} \\ \\ &=\frac{ie^{-ix}e^z - ie^{ix}e^{-z}}{2} \end{align} \] ●実数の場合, \(z=0 \Rightarrow e^{-z}=1,　e^z=1\)

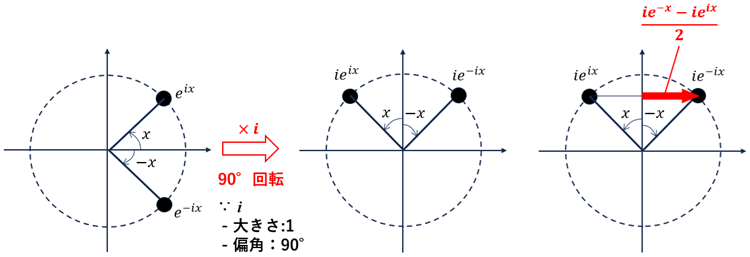
　\(x\) が変化しても赤矢印は -1 ～ +1 の範囲でしか変化しない。


●複素数の場合 (\(z \neq 0\))


　\(z\) の値を変更すると、赤矢印の長さが 1 を超える場合がある。
　2辺の長さが \(e^z\) と \(e^{-z}\)。間の角度が \(2x\)。
　余弦定理より、対辺の長さは \(\sqrt{(e^z)^2+(e^{-z})^2-2e^ze^{-z}\cos(2x)}\)。
　\(|\sin(x+iz)|\) はその半分。


　\(\cos\) も同様･･･