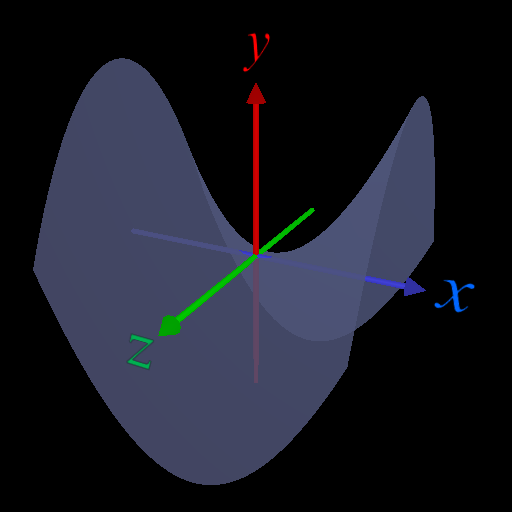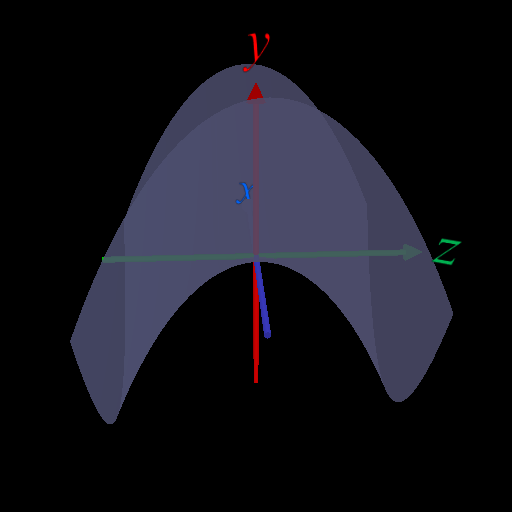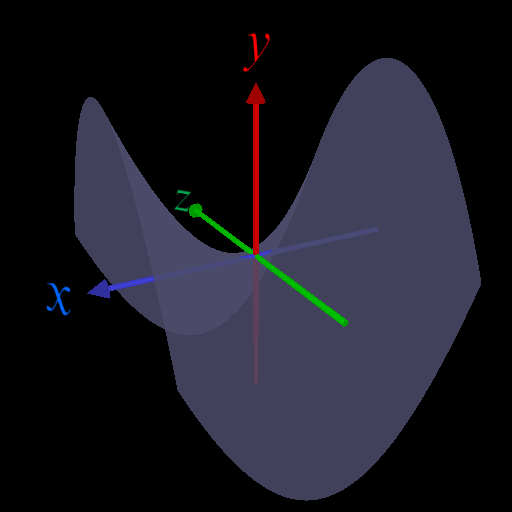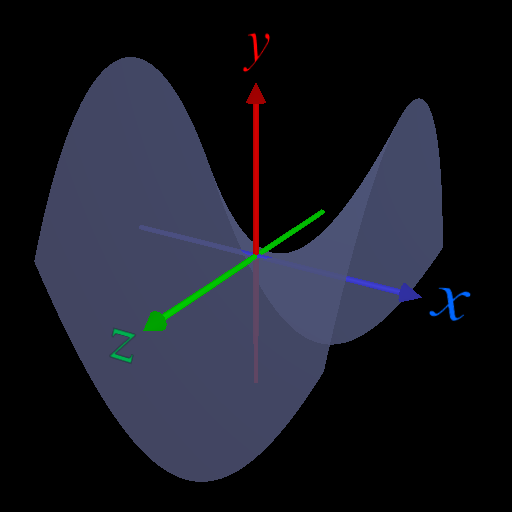
定義域, 値域を複素数に広げると、\(y^2 \geq 0\) は成り立たない。
・値域が複素数になると、大小関係は言えないが・・・
\[
y^2 = (x+iz)^2 = x^2 - z^2 + i・2xz
\]
・\(x\) 軸上(\(z=0\)), \(z\)軸上(\(x=0\))では関数値は虚部が0(=実数)になるので大小関係を議論できる。

\(x\) 軸上では \(z=0 \Rightarrow (x+iz)^2\) の実部: \(x^2 - z^2 \Rightarrow x^2 \geq 0\)
\(z\) 軸上では \(x=0 \Rightarrow (x+iz)^2\) の実部: \(x^2 - z^2 \Rightarrow -z^2 \leq 0\)
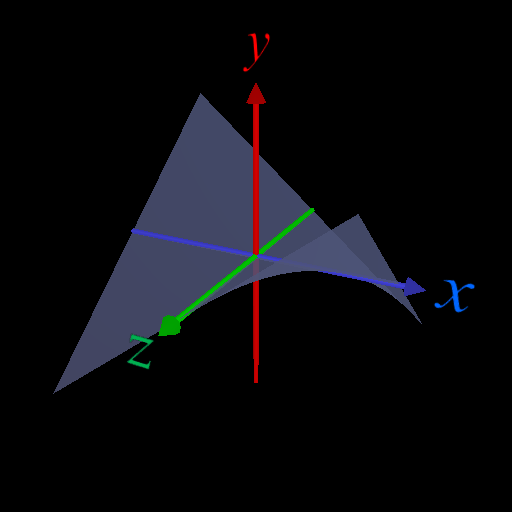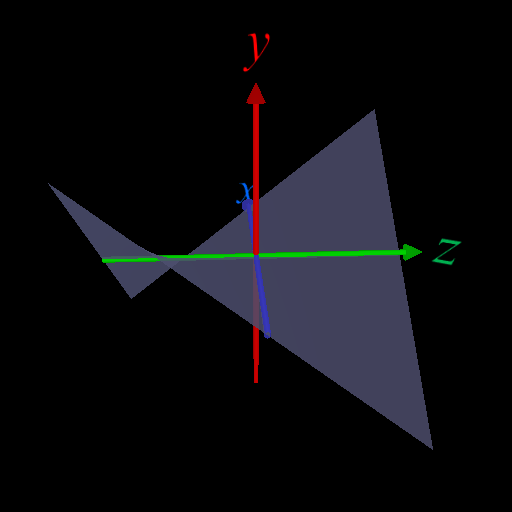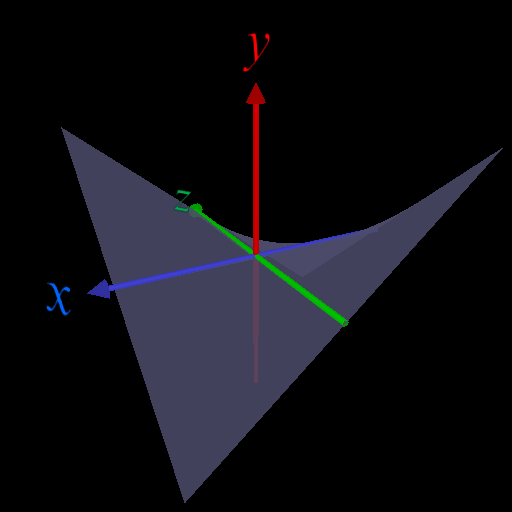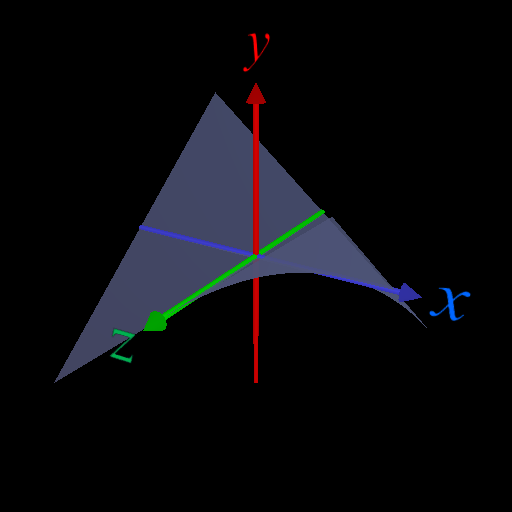
\(x\) 軸上、\(z\) 軸上では \((x+iz)^2\) の虚部: \(2xz = 0\)
\(x\) 軸上、\(z\) 軸上では \((x+iz)^2\) は実数になり、\(x\) 軸上では\(\geq 0\), \(z\)軸上では\(\leq 0\) となる。