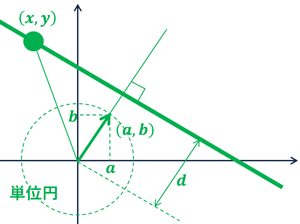
・\(xy\) 平面上の直線の方程式:\(ax+by+c=0 (a,b)\neq (0,0)\)の導出

・直線上の任意の点を \((x,y)\)
・直線の法線を \((a,b)\) ・・・ 大きさ1に正規化されている
とすると、\((x,y)\) と \((a,b)\) の内積は、直線と原点の距離 \(d\) になる。
\((x,y)\cdot(a,b)=ax+by=d\)
\(d\) を移項して \(-d=c\) と置くと上の式が導かれる。
\(y=ax+b\) 表現だと、垂直線で傾き \(a\) が \(\infty\) となり別扱いが必要だが、上の表現ではその必要がない。
\((a,b)\neq(0,0)\) は直線の法線がゼロベクトルになってしまう場合を除外している。