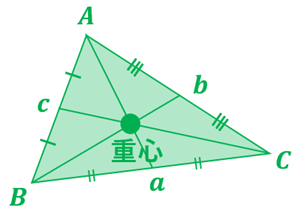
三角形の 重心 は、3本の中線(各頂点と対辺の中点を結ぶ線分)が交わる点のこと。

(準備)
・三角形の頂点を \(A,B,C\)
・各頂点の対辺の中点を \(a,b,c\)
とする。
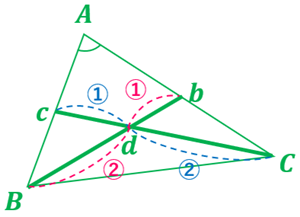
①中点 \(c,b\) を線分でつなぐと \(\triangle ABC\) と \(\triangle Acb\) は相似形になる。
(ニ辺の比が同じで, 間の角度が同じ)
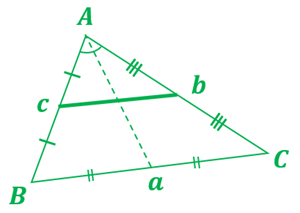
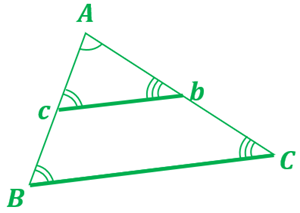
②同位角が同じので線分 \(cb\) と線分 \(BC\) は平行になる。
③錯角,対角は同じなので \(\triangle dBC\) と \(\triangle dbc\) は相似になる。
(\(cb:BC=1:2\) なので相似比 1:2)
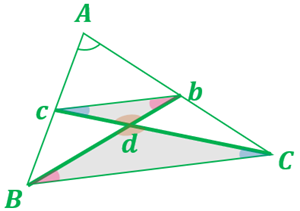
④2つの中線 \(Bb, Cc\) はそれぞれ 1:2 の点で交わる。
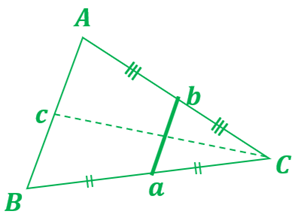
⑤中点 \(a,b\) を線分で結ぶ。
⑥ ①~④と同様の議論により, \(Aa,Bb\) はそれぞれ 1:2 の点で交わる。
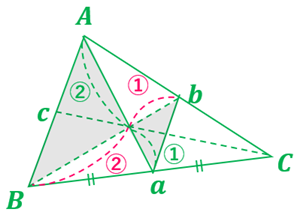
⑦ ④と⑥に出てくる中線 \(Bb\) を 1:2 に内分する点は同一の点なので、3本の中線は1点で交わることが確認できた。
① 点 \((x_1,y_1)\) と点 \((x_2,y_2)\) を結ぶ線分を \(m:n\) に内分する点を考える。
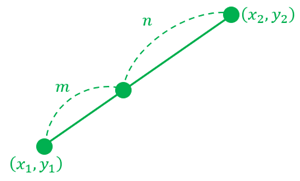
② \(x\) 座標を考えると, 2つの相似な直角三角形の相似比から、内分点の\(x\)座標は以下のようになる。
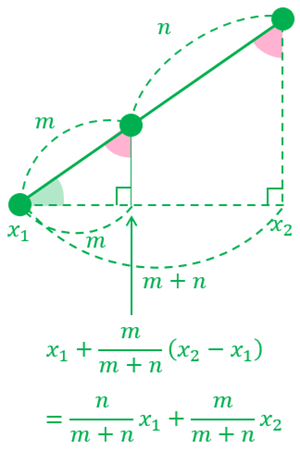
③ \(y\)座標も同様に以下のようになる。
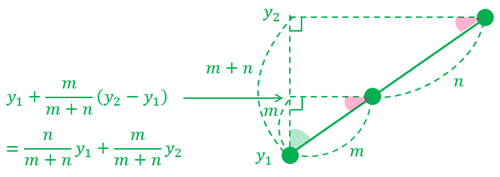
(準備)
・\(A\) の座標を \((x_a,y_a)\)
・\(B\) の座標を \((x_b,y_b)\)
・\(C\) の座標を \((x_c,y_c)\)
とする。
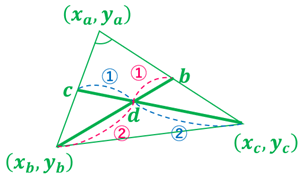
① 中点 \(c\) の座標: \(\left(\frac{x_a+x_b}{2},\frac{y_a+y_b}{2}\right)\)
② 頂点\(C\) と中点 \(c\) を 2:1 に内分する点:
\(\left(\frac{\cancel{2}}{3}\frac{x_a+x_b}{\cancel{2}}+\frac{1}{3}x_c,\frac{\cancel{2}}{3}\frac{y_a+y_b}{\cancel{2}}+\frac{1}{3}y_c\right)=\left(\frac{x_a+x_b+x_c}{3},\frac{y_a+y_b+y_c}{3}\right)\)