この章は、本書で扱われる主要な概念の導入部です。これらのトピックについて、簡潔に解説します。正確で明確な定義、綿密な代数計算、そして洗練された推定アルゴリズムの解説は、本書の第2章以降で行います。本章全体を通して、これらの章への具体的な参照は示しません。
射影変換は誰もがよく知っています。絵を見ると、正方形ではない正方形や、円ではない円が見えます。これらの平面物体を絵に写す変換は、射影変換の一例です。
では、射影変換によって幾何学のどのような特性が保存されるのでしょうか?確かに、形状は保存されません。円が楕円のように見える場合があるからです。長さも保存されません。円の2つの直交する半径は、射影変換によって異なる量だけ引き伸ばされるからです。角度、距離、距離の比など、これらはどれも保存されません。射影変換によって保存される幾何学はほとんどないように見えるかもしれません。しかし、保存される特性は直線性です。これは写像における最も一般的な要件であり、平面の射影変換とは、平面上の点の写像において直線が保存されるものすべてであると定義できます。
なぜ射影幾何学が必要なのかを理解するために、まずはおなじみのユークリッド幾何学から見ていきましょう。ユークリッド幾何学は、物体の角度や形状を記述する幾何学です。ユークリッド幾何学には、ある大きな点で厄介な点があります。直線の交差など、幾何学の基本概念を理解するために、例外を設け続ける必要があるのです。2本の直線(ここでは2次元幾何学を考えています)はほぼ常に1点で交わりますが、そうならない直線のペアも存在します。これを平行線と呼びます。この問題を回避するための一般的な解釈上の手段は、平行線が「無限遠で」交わると言うことです。しかし、これは必ずしも説得力があるわけではなく、無限遠は存在せず、都合の良いフィクションに過ぎないという別の格言と矛盾します。この問題を回避するには、ユークリッド平面を拡張し、平行線が交わる無限遠点を追加し、それらを「理想点」と呼ぶことで無限遠に関する問題を解決します。
これらの無限遠点を加えることで、馴染みのあるユークリッド空間は、射影空間という新しいタイプの幾何学的対象へと変換されます。これは非常に便利な考え方です。なぜなら、距離、角度、点、直線、入射といった概念を含むユークリッド空間の性質はよく知られているからです。射影空間にはそれほど不思議なところはありません。ユークリッド空間の単なる拡張であり、2本の直線は常に1点で交わりますが、時には謎めいた無限遠点で交わることもあります。
座標 ユークリッド2次元空間の点は、実数の順序付きペア \((x, y)\) で表されます。このペアに座標を追加して、\((x, y, 1)\) という組を作り、同じ点を表すと宣言します。最後の座標を追加または削除するだけで、点の表現を切り替えられるので、これは一見無害に思えます。ここで、最後の座標がなぜ1でなければならないのかという重要な概念的ステップに進みます。結局のところ、他の2つの座標はそれほど制約されていません。では、座標の組 \((x, y, 2)\) はどうでしょうか。ここで定義を行い、\((x, y, 1)\) と \((2x, 2y, 2)\) は同じ点を表し、さらに、任意の非ゼロ値 \(k\) に対して、\((kx, ky, k)\) も同じ点を表します。正式には、点は座標三組の同値類によって表されます。つまり、2つの三組が公倍数だけ異なる場合、それらは同値となります。これらは点の同次座標と呼ばれます。座標三組 \((kx, ky, k)\) が与えられた場合、k で割って \((x, y)\) を得ることで元の座標を復元できます。
読者は、\((x, y, 1)\) が座標ペア \((x, y)\) と同じ点を表す一方で、\((x, y, 0)\) に対応する点がないことに気付くでしょう。最後の座標で割ると、無限遠点である \((x/0, y/0)\) が得られます。このようにして無限遠点が生じます。無限遠点は、最後の座標が 0 となる同次座標で表される点です。
2次元ユークリッド空間において、点を同次ベクトルとして表現することで射影空間に拡張する方法を一度見てきましたが、どの次元でも同じようにできることは明らかです。ユークリッド空間 \(\mathbb R^n\) は、点を同次ベクトルとして表現することで射影空間 \(\mathbb P^n\) に拡張できます。2次元射影空間における無限遠点は直線を形成し、通常は無限遠直線と呼ばれます。3次元では、無限遠点は平面を形成します。
同質性 古典的なユークリッド幾何学では、すべての点は同一です。区別される点は存在しません。空間全体が同質です。座標を追加すると、一見すると1つの点が原点として選ばれるように見えます。しかし、これは選択された特定の座標系による偶然の産物に過ぎないことを認識することが重要です。別の点を原点と見なす、平面を座標化する別の方法を見つけることも可能でしょう。実際、ユークリッド空間において、軸を別の位置に移動および回転させる座標変換を考えることができます。これは、空間自体が別の位置に移動および回転すると考えることもできます。この操作はユークリッド変換として知られています。
より一般的な変換は、\(\mathbb R^n\) に線形変換を適用し、続いてユークリッド変換によって空間の原点を移動させるものです。これは、空間が移動、回転し、最終的に異なる方向に異なる比率で線形に伸びると考えることができます。結果として得られる変換はアフィン変換と呼ばれます。
ユークリッド変換またはアフィン変換の結果、無限遠点は無限遠点のままです。そのような点は、少なくとも集合としては、何らかの形で変換によって保存されます。ユークリッド幾何学やアフィン幾何学の文脈において、それらは何らかの形で区別され、特別な意味を持ちます。
射影幾何学の観点から見ると、無限遠点は他の点と何ら変わりありません。ユークリッド空間が一様であるのと同様に、射影空間も一様です。同次座標表現において無限遠点の最終座標が 0 になるという性質は、座標系の選択による偶然に他なりません。ユークリッド変換やアフィン変換と同様に、射影空間の射影変換を定義できます。ユークリッド空間 \(\mathbb R^n\) の線型変換は、点の座標に行列の乗算を適用することで表されます。同様に、射影空間 \(\mathbb P^n\) の射影変換は、点 (\((n + 1)\) ベクトル) を表す同次座標の写像であり、座標ベクトルに非特異行列が乗じられます。このような写像では、無限遠点 (最終座標が 0) は任意の他の点に写像されます。無限遠点は保存されません。したがって、射影空間\(\mathbb P^n\)の射影変換は、同次座標の線型変換で表されます。 \[ X^\prime=H_{(n+1)\times (n+1)}X \]
コンピュータビジョンの問題において、射影空間は現実の3次元世界を3次元射影空間に拡張することで、その世界を表現する便利な方法として用いられます。同様に、通常は世界を2次元表現に投影することで形成される画像は、便宜上、2次元射影空間に存在すると考えられるように拡張されます。実際には、現実世界とその画像は無限遠点を含まないため、画像内の無限遠直線と世界内の無限遠平面といった架空の点がどれなのかを常に把握しておく必要があります。そのため、私たちは通常射影空間を扱いますが、無限遠直線と無限遠平面は何らかの意味で特別な意味を持つことを認識しています。これは純粋射影幾何学の精神に反しますが、実際の問題には有用です。一般的に、私たちは射影空間内のすべての点を、必要に応じて同等に扱い、必要に応じて空間内の無限遠直線または画像内の無限遠平面のみを対象とすることで、両方の利点を享受しようとします。
ユークリッド空間に無限遠直線(または無限遠平面)を加えることで射影空間が得られることを見てきました。ここでは、逆の過程を考察します。この議論は主に2次元および3次元の射影空間についてです。
アフィン幾何学 ここでは、射影空間は元来同次であり、特定の座標系は存在しないという立場をとります。このような空間では、直線の平行性という概念は存在しません。なぜなら、平行線(三次元の場合は平面)は無限遠点で交わるからです。射影空間では、どの点が無限遠点にあるかという概念は存在せず、すべての点は等しく作られるからです。したがって、平行性は射影幾何学の概念ではないと言えます。平行性について議論するのは全く無意味です。
この概念を理解するには、ある特定の直線を選び出し、それを無限遠直線と定義する必要があります。こうすることで、すべての点は等しく作られているものの、ある点は他の点よりも等しくなっているという状況が生まれます。まず、白紙を1枚用意し、それが無限遠まで伸びて射影空間 \(\mathbb P^2\) を形成すると想像してみましょう。私たちが見ているのは、この空間のほんの一部であり、通常のユークリッド平面の一部によく似ています。さて、紙に直線を描き、これを無限遠直線と定義しましょう。次に、この線で交差する2本の直線を描きます。これらの直線は「無限遠直線」で交わるので、平行であると定義します。これは、無限平面を見るときに見えるものと似ています。地球の非常に平坦な地域で撮影された写真を想像してみてください。平面上の無限遠点は、画像では地平線として現れます。鉄道の線路などの線も、画像では地平線で交わる線として現れます。地平線 (空の画像) より上にある画像内の点は、ワールド平面上の点とは明らかに対応していません。ただし、対応する光線をカメラの背後に後方に延長することを考えると、カメラの背後の点で平面と交わります。したがって、画像内の点とワールド平面内の点の間には 1 対 1 の関係があります。ワールド平面内の無限遠の点は画像内の実際の地平線に対応し、ワールド内の平行線は地平線で交わる線に対応します。私たちの観点からすると、ワールド平面とその画像は、射影平面の幾何学と区別された直線の別の見方にすぎません。射影平面と区別された直線の幾何学はアフィン幾何学として知られており、一方の空間の区別された直線をもう一方の空間の区別された直線にマッピングする射影変換はすべてアフィン変換として知られています。
特別な直線を「無限遠直線」と定義することで、平面上の直線の平行性を定義できます。しかし、平行性を定義できれば、他の概念も理解しやすくなります。例えば、平行線上の2点間の間隔が等しいと定義できます。例えば、A、B、C、Dが点であり、直線ABとCDが平行である場合、直線ACとBDも平行であれば、2つの区間ABとCDの長さは等しいと定義できます。同様に、同じ直線上の2つの区間が等しい場合、その2つの区間の長さは、平行線上に2つの区間の長さが等しい別の区間が存在する場合に等しくなります。
ユークリッド幾何学 射影平面上の特定の直線を区別することで、平行性の概念が得られ、それに伴いアフィン幾何学も生まれます。アフィン幾何学は射影幾何学の特殊化とみなされ、特定の直線(または次元によっては平面)を取り出し、それを無限遠直線と呼びます。
次にユークリッド幾何学に目を向け、無限遠直線または無限遠平面の特定の特徴を取り出すことで、アフィン幾何学がユークリッド幾何学になることを示します。その際、本書で最も重要な概念の一つである絶対円錐曲線を導入します。
まず二次元幾何学、円から考えてみましょう。円はアフィン幾何学の概念ではないことに注意してください。平面を任意の方向に引き伸ばすと、無限遠直線は保存されますが、円は楕円に変化するためです。したがって、アフィン幾何学では円と楕円は区別されません。
しかし、ユークリッド幾何学では、これらは明確に区別され、重要な違いがあります。代数的には、楕円は2次方程式で記述されます。したがって、2つの楕円は最も一般的には4点で交差することが予想され、事実です。しかし、2つの異なる円は2点以上で交差することはあり得ないことは幾何学的に明らかです。代数的には、ここでは2つの2次曲線を交差させている、つまり2つの二次方程式を解いていることになります。4つの解が得られることが期待されます。問題は、円が2点でしか交差しないことの何が特別なのかということです。
この問いへの答えは、もちろん、二つの円が二つの複素点で交わる、二つの解が存在するということです。この二つの点を見つけるのに、それほど遠くまで探す必要はありません。
同次座標\((x, y, w)\)における円の方程式は次の形式になります。 \[ (x − aw)^2 + (y − bw)^2 = r^2w^2 \] これは、中心が同次座標で \((x_0, y_0,w_0)^T = (a, b, 1)^T\) で表される円を表しています。点 \((x, y,w)^T = (1,±i, 0)^T\) がこのような円のすべてに存在することが簡単に確認できます。この興味深い事実を繰り返すと、すべての円は点 \((1,±i, 0)^T\) を通るため、任意の 2 つの円の交点に存在します。最終的な座標は 0 なので、これら 2 つの点は無限遠直線上にあります。明らかな理由から、これらは平面の円点と呼ばれます。2 つの円点は複素数ですが、2 つの実方程式 \(x^2 + y^2 = 0; w = 0\) を満たすことに注意してください。
この観察は、ユークリッド幾何学をどのように定義するかについての手がかりを与えます。ユークリッド幾何学は、射影幾何学から、まず無限遠直線を選び出し、次にこの直線上にある円点と呼ばれる 2 つの点を選ぶことによって生じます。もちろん円点は複素点ですが、ほとんどの場合、これについてあまり気にする必要はありません。ここで、円は 2 つの円点を通る任意の円錐曲線 (2 次方程式で定義される曲線) として定義できます。標準ユークリッド座標系では、円点は座標 \((1,±i, 0)^T\) を持つことに注意してください。ただし、射影平面にユークリッド構造を割り当てる際には、任意の直線とその直線上の任意の 2 つの (複素) 点を、無限遠直線と円点として指定できます。
この視点を適用する例として、一般的な円錐曲線は平面上の任意の5点を通ることが分かります。これは、一般的な二次方程式\(ax^2 + by^2 + . . . + fw^2 = 0\)の係数の数を数えれば分かります。一方、円は3点のみで定義されます。別の見方をすれば、円は2つの特別な点(円点)と他の3点を通る円錐曲線であり、したがって他の円錐曲線と同様に、それを一意に特定するには5点が必要です。
二つの円点を選り分けることで、おなじみのユークリッド幾何学の全体が得られることは驚くべきことではありません。特に、角度や長さの比といった概念は、円点を用いて定義できます。しかし、これらの概念は、後の章で述べるように、ユークリッド平面の座標系を用いて定義するのが最も容易です。
3次元ユークリッド幾何学 ユークリッド平面は、無限遠直線と2つの円弧点を指定することにより、射影平面を用いて定義されることを理解しました。同じ考え方は3次元幾何学にも適用できます。2次元の場合と同様に、球面とその交差を注意深く観察してみましょう。2つの球面は円で交差し、代数的に示唆されるような一般的な4次曲線や、2つの一般的な楕円体(またはその他の二次曲面)のように交差することはありません。この考え方から、同次座標系 \((X, Y, Z, T)^T\) において、すべての球面は無限遠平面と曲線で交差し、その式は \(X^2 + Y^2 + Z^2 = 0; T = 0\) となることがわかります。これは、無限遠平面上に存在する2次曲線(円錐曲線)であり、複素点のみで構成されています。これは絶対円錐曲線として知られており、この本で重要な幾何学的実体の 1 つです。特に、後述するように、カメラのキャリブレーションとの関連が重要です。
絶対円錐曲線は、上記の式によってユークリッド座標系においてのみ定義されます。一般に、3次元ユークリッド空間は、特定の平面を無限遠平面として選び、その平面上に存在する特定の円錐曲線を絶対円錐曲線と指定することによって、射影空間から導かれると考えることができます。これらの実体は、射影空間の座標系を用いて非常に一般的な記述を持つ場合があります。
ここでは絶対円錐曲線がどのようにして完全なユークリッド 3D 幾何学を決定するかについては詳しく説明しません。1 つの例で十分でしょう。空間における直線の垂直性はアフィン幾何学では有効な概念ではありませんが、ユークリッド幾何学に属します。直線の垂直性は、次のように絶対円錐曲線によって定義できます。直線を無限遠平面と交わるまで延長すると、2 つの直線の方向と呼ばれる 2 つの点が得られます。直線の垂直性は、2 つの方向と絶対円錐曲線の関係によって定義されます。2 つの方向が絶対円錐曲線に関して共役点である場合、直線は垂直です (図 3.8) を参照)。共役点の幾何学と代数的表現は、セクション 2.8.1 で定義されています。簡単に言えば、絶対円錐曲線が3×3対称行列\(\Omega_\infty\)で表され、方向が点\(d_1\)と\(d_2\)である場合、\(d_1^T\Omega_\infty d_2=0\)のとき、それらは\(\Omega_\infty\)に関して共役である。より一般的には、角度は任意の座標系における絶対円錐曲線を用いて定義することができ、式(3.23)で表される。
この本の主なテーマの 1 つは、画像形成のプロセス、つまり 3 次元世界の 2 次元表現の形成と、画像に現れるものの 3D 構造について何を推測できるかという点です。
三次元世界から二次元画像への投影は、ある次元を失う投影プロセスです。このプロセスをモデル化する一般的な方法は、中心投影です。中心投影では、空間内の一点から三次元世界の一点に引かれた光線が、空間内の固定点(投影の中心)を通過します。この光線は、像面として選択された空間内の特定の平面と交差します。光線と像面の交点は、その点の像を表します。三次元構造が平面上にある場合、次元の損失はありません。
このモデルは、カメラの単純なモデルと一致しています。カメラのモデルでは、世界のある点から発せられた光線がカメラのレンズを通過し、フィルムまたはデジタル機器に入射して、その点の画像を生成します。焦点やレンズの厚さなどの影響を無視すると、すべての光線がレンズの中心という一点を通過すると近似するのが妥当です。
射影幾何学を画像化プロセスに適用する場合、世界を \(\mathbb R^3\) と無限遠点に等しい3次元射影空間としてモデル化するのが一般的です。同様に、画像のモデルは2次元射影平面\(\mathbb P^2\) です。中心射影は、\(\mathbb P^3\) から \(\mathbb P^2\) への単純な写像です。 \(\mathbb P^3\) 内の点を同次座標 \((X, Y, Z, T)^T\) で表し、投影の中心を原点 \((0, 0, 0, 1)^T\) とすると、\(X, Y\) と \(Z\) は固定で \(T\) が変化するすべての点 \((X, Y, Z, T)^T\) の集合が、投影の中心を通る単一の光線を形成し、したがってすべて同じ点に写像されることがわかります。したがって、\((X, Y, Z, T)\) の最終的な座標は、点がどこに写像されるかとは無関係です。実際、像点は \(\mathbb P^2\) 内の同次座標 \((X, Y, Z)^T\) の点です。したがって、この写像は3次元同次座標の写像で表現でき、ブロック構造 \(P = [I_{3×3}|0_3]\) を持つ3 × 4行列 \(P\) で表されます。ここで、\(I_{3×3}\) は3 × 3の単位行列、\(0_3\) は零3次元ベクトルです。投影中心と画像内の射影座標系が異なることを考慮に入れると、最も一般的な画像投影は、\(\mathbb P^3\) 内の点の同次座標に作用し、それを \(\mathbb P^2\) 内の画像点に写像する、階数3の任意の3×4行列で表されます。この行列 \(P\) はカメラ行列と呼ばれます。
要約すると、空間内の点に対する射影カメラの作用は、同次座標の線形写像で次のように表現できます。 \[ \left( \begin{array}{c} x\\ y\\ w\\ \end{array} \right) =P_{3\times 4} \left( \begin{array}{c} X\\ Y\\ Z\\ T\\ \end{array} \right) \] さらに、すべての点が平面(ここでは平面 \(Z = 0\) とします)上にある場合、線形写像は次のように簡約されます。 \[ \left( \begin{array}{c} x\\ y\\ w\\ \end{array} \right) =H_{3\times 3} \left( \begin{array}{c} X\\ Y\\ T\\ \end{array} \right) \] これは射影変換です。
カメラを点として扱う。
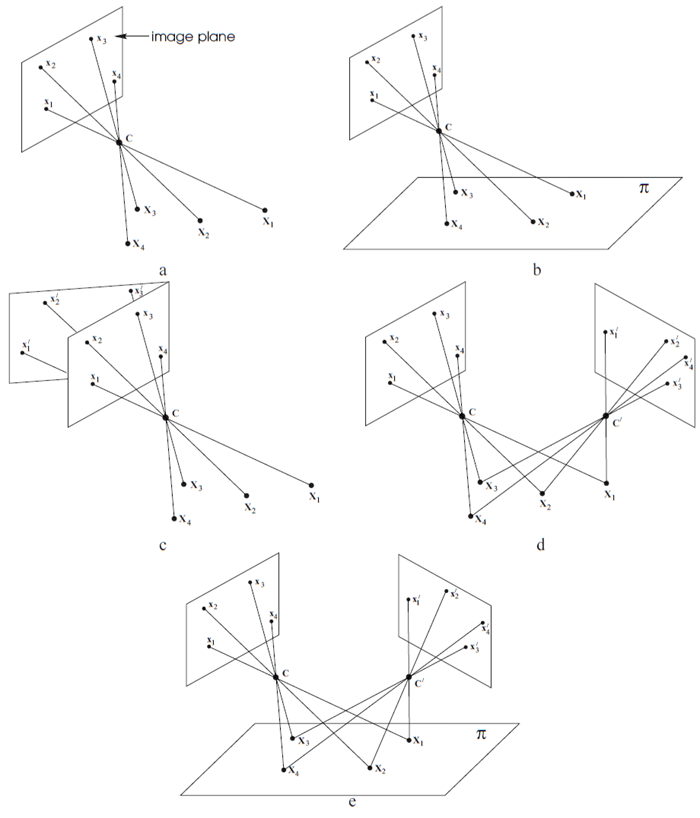
中心投影では、\(\mathbb P^3\) 内の点は \(\mathbb P^2\) 内の点に写像されます。投影の中心を通る光線上のすべての点は、画像内の同じ点に投影されます。画像投影の目的上、このような光線上のすべての点は等しいとみなすことができます。さらに一歩進んで、投影の中心を通る光線が画像点を表すと考えることもできます。したがって、すべての画像点の集合は、カメラの中心を通る光線の集合と同じです。点 \((0, 0, 0, 1)^T\) から点 \((X, Y, Z, T)^T\) を通る光線を、最初の3つの座標 \((X, Y, Z)^T\) で表すと、任意の定数 \(k\) に対して、光線 \(k(X, Y, Z)^T\) が同じ光線を表すことが容易にわかります。したがって、光線自体は同次座標で表されます。実際、光線は2次元の光線空間を構成します。光線の集合自体は、画像空間 \(\mathbb P^2\) の表現と考えることができます。この画像の表現において重要なのはカメラ中心だけです。なぜなら、これだけで画像を形成する光線の集合が決まるからです。同じ投影中心からの画像形成を表す異なるカメラ行列は、画像を形成する光線の集合の異なる座標系のみを反映します。したがって、空間内の同じ点から撮影された2つの画像は、射影的に等価です。画像内の点の計測を開始するときにのみ、画像の特定の座標系を指定する必要があります。そして、その際に初めて、特定のカメラ行列を指定する必要が生じます。つまり、ここでは視野角を無視しますが、同じカメラ中心で取得されたすべての画像は等価です。つまり、3D点やカメラ中心の位置に関する情報がなくても、射影変換によって互いにマッピングできます。これらの問題は図1.1に示されています。

図 1.1 カメラ中心が重要です。(a) 画像の形成: 画像点 \(x_i\) は、空間点 \(X_i\) からカメラ中心 \(C\) を通る光線と平面との交点です。(b) 空間点が共面の場合、ワールド平面と画像平面の間には射影変換 \(x_i = H_{3×3}X_i\) が存在します。(c) 同じカメラ中心を持つすべての画像は、射影変換 \(x_i^\prime= H_{3×3}^\prime x_i\) によって関連付けられます。(b) と (c) を比較してください。どちらの場合も、平面は中心を通る光線によって互いにマッピングされています。(b) ではマッピングはシーンと画像平面の間で行われ、(c) では 2 つの画像平面の間で行われます。(d) カメラ中心が移動する場合、(e) すべての空間点が共面である場合を除き、画像は一般に射影変換によって関連付けられません。
キャリブレーションされたカメラ 画像と世界との間のユークリッド関係を完全に理解するには、それらの相対的なユークリッド幾何学を表現する必要があります。既に述べたように、3次元世界のユークリッド幾何学は、\(\mathbb P^3\) 内の特定の平面を無限遠平面として指定し、その平面内の特定の円錐曲線 \(\Omega\) を絶対円錐曲線として指定することによって決定されます。無限遠平面上に配置されていないカメラの場合、世界における無限遠平面は画像平面に1対1で写像されます。これは、画像内の任意の点が、無限遠平面と一点で交わる空間内の光線を定義するためです。したがって、世界における無限遠平面は、画像について何も新しいことを教えてくれません。しかし、絶対円錐曲線は無限遠平面内の円錐曲線であるため、画像内の円錐曲線に投影される必要があります。結果として得られる画像曲線は、絶対円錐曲線の像、またはIACと呼ばれます。画像内で IAC の位置がわかっている場合、カメラはキャリブレーションされていると言えます。
キャリブレーションされたカメラでは、画像内の2点から逆投影された2本の光線間の角度を測定できます。空間内の2本の線の間の角度は、絶対円錐曲線を基準として、それらが無限遠平面と交わる位置によって決まることを既に説明しました。キャリブレーションされたカメラでは、無限遠平面と絶対円錐曲線 \(\Omega_\infty\) は、画像平面とIAC(\(\omega\) と表記)に1対1で投影されます。2つの画像点と \(\omega\) の投影関係は、逆投影された光線と無限遠平面の交点と \(\Omega_\infty\) の関係と完全に一致します。したがって、IAC がわかれば、画像内で直接測定することで光線間の角度を測定できます。このように、キャリブレーションされたカメラであれば、光線間の角度を測定したり、画像パッチによって表される視野を計算したり、画像内の楕円が円錐に逆投影されるかどうかを判断したりすることができます。後ほど、これが再構成されたシーンのユークリッド構造を決定するのに役立つことを見ていきます。
例1.1. 絵画からの3D再構成
射影幾何学の手法を用いることで、多くの場合、単一の画像からシーンを再構成することが可能です。しかし、これは、撮影されたシーンについて何らかの仮定を置かずには実現できません。典型的な手法としては、平行線や消失点などの特徴を分析し、シーンのアフィン構造を判定することが挙げられます。例えば、画像内の観測面の無限遠直線を決定するなどです。シーン内で観測される角度、特に直交する直線や平面に関する知識(または仮定)は、アフィン再構成をユークリッド再構成へと昇格させるのに利用できます。
このような技術を完全に自動化することはまだ不可能です。しかし、射影幾何学の知識をシステムに組み込むことで、ユーザーガイドによる単一視点からのシーン再構成が可能になる可能性があります。
このような技術は、古典絵画から派生した3Dテクスチャマッピングされたグラフィックモデルの復元に用いられてきました。ルネサンス以降、極めて正確な遠近法を用いた絵画が制作されました。図1.2は、そのような絵画から復元されたものです。

図1.2. 単一視点からの再構成。(a) 原画「書斎の聖ヒエロニムス」(1630年)、ヘンドリック・ファン・ステーンウィック(1580-1649)、ジョセフ・R・リトマン個人コレクション、アムステルダム、オランダ。(b) (c) (d) 絵画から作成された3Dモデルの図。
さて、本書の主要なトピックの一つ、複数の画像からシーンを再構成する方法について考察します。まずは、最も単純な例として2枚の画像からシーンを再構成するケースについて考えます。数学的な抽象化のため、ここでは点のみで構成される「シーン」に議論を限定します。
本書で紹介する多くのアルゴリズムへの通常の入力は、点の対応関係の集合です。したがって、2視点の場合、2枚の画像における対応関係の集合 \(x_i\leftrightarrow x_i^\prime\) を考慮します。カメラ行列 \(P\) と \(P^\prime\) と、これらの画像対応関係(\(PX_i = x_i\) および \(P^\prime X_i = x_i^\prime\) )を生み出す3D点集合 \(X_i\) が存在すると仮定します。したがって、点 \(X_i\) は、与えられた2つのデータ点に投影されます。ただし、カメラ(投影行列 \(P\) と \(P^\prime\) で表される)も点 Xi も既知ではありません。これらを特定することが私たちの課題です。
最初から明らかなのは、点の位置を一意に特定することは不可能だということです。これは、どんなに多くの画像が与えられても、また点の対応データ以上のものを持っていても、常に存在する一般的な曖昧性です。例えば、立方体の画像が複数あっても、その絶対位置(アディスアベバのナイトクラブにあるか、それとも大英博物館にあるか)、向き(どちらの面が北を向いているか)、あるいは大きさを判断することは不可能です。これを、再構成はせいぜい世界の相似変換までしか不可能ではないと表現します。しかし、2台のカメラのキャリブレーションについて何かが分かっていない限り、再構成における曖昧性は、より一般的なクラスの変換、つまり射影変換によって表現されることがわかります。
この曖昧さは、投影された画像ポイントを変更せずに、各ポイント \(X_i\) と各カメラ行列 \(P_j\) の右側に射影変換 (4 × 4 行列 \(H\) で表される) を適用できるため発生します。 \[ P_jX_i = (P_jH^{−1})(HX_i) \tag{1.1} \] どちらか一方の点群とカメラ行列を選択する強い理由はありません。\(H\)の選択は本質的に任意であり、再構成には射影的曖昧性がある、あるいは射影再構成であると言います。
しかし、朗報なのは、これが最悪の事態に過ぎないということです。避けられない射影的曖昧さを除けば、2つの視点から点の集合を再構成することは可能です。ただし、これを言えるためには、いくつかの条件が必要です。点の数は十分に多く、少なくとも7つである必要があります。また、それらの点は、明確に定義された様々な臨界配置のいずれかに含まれてはなりません。
2つの視点から点集合を再構成するための基本的なツールは基礎行列であり、これは、像点 \(x\) と \(x^\prime\) が同じ3次元点の像となる場合に、それらが従う制約を表す。この制約は、2つの視点、像点、および空間点のカメラ中心が同一平面にあることから生じる。基礎行列 F が与えられた場合、対応する点のペア \(x_i\leftrightarrow x^\prime\) は、 \[ {x_i^\prime}^TFx_i = 0 \] ここで、\(F\) は階数2の3×3行列です。これらの方程式は行列 \(F\) の要素について線形であり、つまり、\(F\) が不明な場合は、点の対応関係の集合から計算できます。
カメラ行列のペア \(P\) と \(P^\prime\) は、基礎行列 \(F\) を一意に決定し、逆に、基礎行列は、3次元の射影的曖昧性を除いて、カメラ行列のペアを決定します。したがって、基礎行列はカメラペアの完全な射影幾何学を包含し、3次元の射影変換によって変化しません。
シーンを再構成するための基礎行列法は非常にシンプルで、以下の手順から成ります。
ここで示すアルゴリズムは概要のみであり、各部分は本書で詳細に検討されています。この簡潔な説明からアルゴリズムをそのまま実装することは推奨しません。
前のセクションでは、点群の2つの視点から点群の再構成とカメラの相対的な配置がどのように可能になるかについて説明しました。再構成は、空間の射影変換と、それに応じたカメラ行列の調整によってのみ可能になります。
このセクションでは、3つの視点の場合を考察します。2つの視点の場合、基本的な代数的実体は基礎行列ですが、3つの視点の場合、この役割は三焦点テンソルによって担われます。三焦点テンソルは、3つの視点における対応する点または線の座標を関連付ける3×3×3の数値配列です。基礎行列が2つのカメラ行列によって決定され、射影変換までそれらを決定するのと同様に、3つの視点の場合、三焦点テンソルは3つのカメラ行列によって決定され、さらに射影変換までそれらを決定します。このように、三焦点テンソルは3台のカメラの相対的な射影幾何学をカプセル化します。
第15章で説明する理由により、テンソルの添え字のいくつかは下付き添字、いくつかは上付き添字と表記するのが一般的です。これらは共変添え字と反変添え字と呼ばれます。三焦点テンソルは \(T_i^{jk}\) の形をとり、2つの上付き添字と1つの下付き添字を持ちます。
3つの視点における画像エンティティ間の最も基本的な関係は、2本の直線と1点の対応関係です。1つの画像内の点 \(x\)と、他の2つの画像内の2本の直線 \(l^\prime\) および \(l^{\prime\prime}\) との間の対応関係 \(x\leftrightarrow l^\prime\leftrightarrow l^{\prime\prime}\) を考えます。この関係は、最初の画像内の \(x\) と、他の2つの画像内の直線\(l^\prime\)および\(l^{\prime\prime}\) 上の点 \(x^\prime\) および \(x^{\prime\prime}\) に対応する空間内の点 \(X\) が存在することを意味します。これらの3つの画像の座標は、三焦点テンソル関係によって次のように関連付けられます。 \[ \sum_{i,j,k}x^il_j^\prime l_k^{\prime\prime}T_i^{jk}=0 \tag{1.2} \] この関係は、テンソルの要素間に単一の線形関係を与えます。このような対応が十分に多ければ、テンソルの要素について線形に解くことができます。幸いなことに、点対応 \(x\leftrightarrow x^\prime\leftrightarrow x^{\prime\prime}\) からより多くの方程式を得ることができます。実際、この状況では、点 \(x^\prime\) と \(x^{\prime\prime}\) を通る任意の直線 \(l^\prime\) と \(l^{\prime\prime}\) を選択して、(1.2) のような関係を生成できます。\(x^\prime\) を通る独立した直線を 2 本、\(x^{\prime\prime}\) を通る独立した直線を 2 本選択することができるため、この方法で 4 つの独立した方程式を得ることができます。このようにして三焦点テンソルを線形に計算するには、合計 7 つの点対応で十分です。非線形法を使用して、最低 6 点の対応から計算できます。
しかしながら、テンソルの27個の要素は独立ではなく、いわゆる内部制約によって関連付けられています。これらの制約は非常に複雑ですが、制約を満たすテンソルは、例えば6点非線形法を用いるなど、様々な方法で計算できます。基礎行列(2視点テンソル)も内部制約を満たしますが、これは比較的単純なもので、要素は \(det F = 0\) に従います。
基礎行列と同様に、三焦点テンソルが分かれば、そこから3つのカメラ行列を抽出し、シーン上の点と線の再構成を得ることができます。これまでと同様に、この再構成は3次元射影変換を除いては一意であり、射影再構成です。
このように、2視点用の手法を3視点にも一般化することができます。再構成にこのような3視点手法を用いることには、いくつかの利点があります。
テンソルベースの手法では、さらに一歩進んで、4つの視点で見える実体を関連付ける4焦点テンソルを定義することができます。しかし、この手法は、内部制約を満たす4焦点テンソルを計算するのが比較的難しいため、ほとんど使用されません。それでも、4つの視点に基づく射影再構成を計算するための非反復的な手法を提供します。ただし、テンソル法は4つ以上の視点には拡張できないため、4つ以上の視点からの再構成はより困難になります。
複数の視点からの再構成には多くの手法が検討されており、本書ではそのうちのいくつかを取り上げます。一つの方法は、3視点または2視点の手法を用いて、シーンを少しずつ再構成することです。この手法はあらゆる画像シーケンスに適用でき、適切な3視点を慎重に選択すれば、通常は成功します。
特定の状況で使用できる手法がいくつかあります。アフィンカメラと呼ばれるより単純なカメラモデルを適用できれば、再構成作業は容易になります。このカメラモデルは、シーンまでの距離がシーンの前後の奥行きの差に比べて大きい場合、透視投影の適切な近似となります。アフィンカメラを含むn個の視点セットのすべてで点の集合が見える場合、よく知られたアルゴリズムである因数分解アルゴリズムを使用して、特異値分解を用いてシーンの構造と特定のカメラモデルの両方を1つのステップで計算できます。このアルゴリズムは非常に信頼性が高く、実装も簡単です。主な難点は、完全な射影モデルではなくアフィンカメラモデルを使用することと、すべての点がすべての視点で見える必要があることです。
この手法は、射影分解として知られる手法で射影カメラに拡張されています。この手法は一般的には満足のいくものですが、すべてのケースで正しい解に収束することを証明することはできません。さらに、すべての点がすべての画像で見える必要があります。
n視点再構成のための他の手法には、様々な仮定が伴います。例えば、すべての視点から見える4つの共面点、あるいはシーケンス内のすべての画像から見える6点または7点といった仮定です。直線運動、平面運動、単軸(ターンテーブル)運動といった特定の運動シーケンスに適用できる手法も開発されています。
一般的な再構成問題に対する主要な手法はバンドル調整です。これは反復的な手法であり、測定データ(点の対応関係)に非線形モデルを当てはめようとします。バンドル調整の利点は、非常に汎用的な手法であり、幅広い再構成問題や最適化問題に適用できることです。バンドル調整は、発見された解が問題の最大尤度解、つまり画像測定の不正確さを考慮したモデルの観点からある意味で最適な解となるように実装できます。
残念ながら、バンドル調整は反復的なプロセスであり、任意の開始点から最適解に収束する保証はありません。再構成手法に関する多くの研究では、バンドル調整の開始点として使用できる、容易に計算可能な非最適解が求められています。再構成には、初期化ステップに続いてバンドル調整を行う手法が一般的に好まれます。バンドル調整は必然的に時間のかかる手法であるという印象が一般的ですが、実際には、慎重に実装すれば非常に効率的です。本書の長大な付録では、バンドル調整の効率的な手法について解説しています。
n視点再構成技術を用いることで、非常に長い画像シーケンスから自動的に再構成を行うことができます。図1.3に、700フレームからの再構成例を示します。
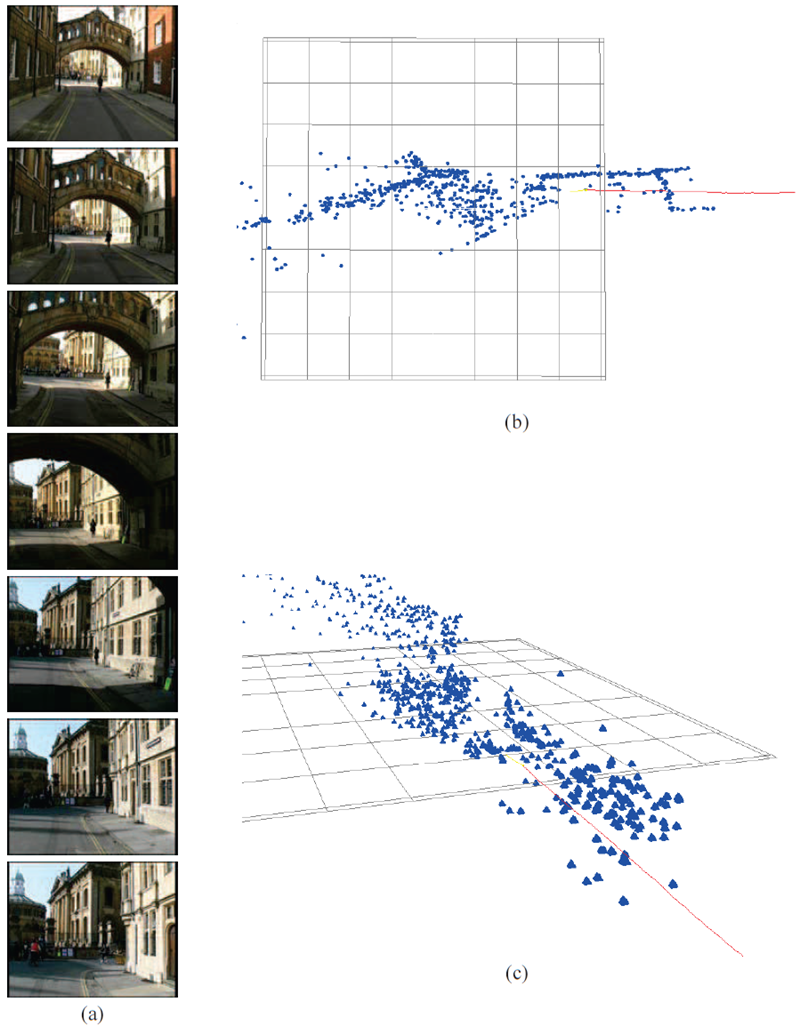
図1.3 再構成。(a) オックスフォードの街路を歩きながら手持ちカメラで撮影した700フレームのシーケンスのうち7フレーム。(b)(c) 再構成された点群とカメラパス(赤い曲線)の2つの視点。
画像セットからの3D再構成について論じました。射影幾何学のもう一つの有用な応用は、移送(Transfer)です。1枚(または複数枚)の画像における点の位置が与えられた場合、その点が集合内の他のすべての画像でどこに現れるかを決定します。これを行うには、まず(例えば)補助的な点の対応関係を用いて、カメラ間の関係を確立する必要があります。再構成が可能である限り、概念的には転送は簡単です。例えば、ある点が2つの視点 \((xとx^\prime)\) で特定されており、3つ目の視点におけるその点の位置 \(x^{\prime\prime}\) を知りたい場合、これは以下の手順で計算できます。
この手順では射影情報のみが必要です。別の方法として、多視点テンソル(基礎行列と三焦点テンソル)を用いて、明示的な3D再構成を行わずに直接点を転送する方法があります。どちらの方法にも利点があります。
カメラがその中心周りに回転するか、シーン上のすべての関心点が平面上にあると仮定します。その場合、適切な多視点関係は、画像間の平面射影変換です。この場合、1枚の画像に映っている点は、他の任意の画像に転送できます。
これまで、キャリブレーションされていないカメラ群で撮影された画像のシーン再構成、つまり転送について検討してきました。このようなカメラでは、焦点距離、画像の幾何学的中心(主点)、そして場合によっては画像内のピクセルのアスペクト比といった重要なパラメータが不明です。各カメラの完全なキャリブレーションが分かっていれば、再構成されたシーンの曖昧さをある程度排除することが可能です。
これまで、カメラやシーンのキャリブレーションに関する情報を必要とせずに実行できる唯一の手法である射影再構成について説明してきました。射影再構成は、ユークリッド世界を見ることに慣れた人間には奇妙に見えるモデルの歪みを伴うため、コンピュータグラフィックスへの応用など、多くの目的には不十分です。例えば、射影変換が単純な物体に引き起こす歪みを図1.4に示します。射影再構成の手法を用いると、図1.4に示すマグカップの可能な形状のいずれかを選択することはできず、射影再構成アルゴリズムは、そこに示されている再構成のいずれかを生成する可能性が他の再構成と同様に高くなります。射影再構成によって、さらにひどく歪んだモデルが生じる可能性もあります。

図1.4. 射影的曖昧性:マグカップ(中央に真の形状を表示)のZ方向への3次元射影変換による再構成。射影歪みの程度が異なる5つのカップの例が示されている。形状は元のものとは大きく異なっている。
物体が正しい(ユークリッド)形状を持つモデルの再構成を得るには、カメラのキャリブレーションを決定する必要があります。これでシーンのユークリッド構造を決定できることは容易にわかります。 既に述べたように、世界のユークリッド構造を決定することは、無限遠平面と絶対円錐曲線を指定することと同等です。実際、絶対円錐曲線は無限遠平面上にあるため、空間内で絶対円錐曲線を見つければ十分です。 ここで、キャリブレーション済みのカメラを用いて世界の射影再構成を計算したと仮定します。定義により、これは各画像におけるIACが既知であることを意味します。i番目の画像において、それを!iで表します。各!iの逆投影は空間における円錐であり、絶対円錐曲線はすべての円錐の交点になければなりません。 2つの円錐は一般に4次曲線で交差しますが、円錐曲線で交差しなければならないことを考えると、この曲線は2つの円錐曲線に分割される必要があります。したがって、2枚の画像から絶対円錐曲線を再構成することは一意ではなく、むしろ一般に2つの解が考えられます。しかし、3枚以上の画像から得られる円錐の交点は一般に一意です。このようにして絶対円錐曲線が決定され、それとともにシーンのユークリッド構造も決定されます。
もちろん、シーンのユークリッド構造が分かっていれば、絶対円錐曲線の位置も分かっています。この場合、それを各画像に投影し直し、各画像のIACを生成してカメラをキャリブレーションすることができます。したがって、カメラのキャリブレーションを知っていることは、シーンのユークリッド構造を決定できることと同等です。
カメラのキャリブレーションに関する情報がなければ、射影再構成よりも優れた結果を得ることは不可能です。任意の数の視点にわたる特徴点の対応関係の集合には、絶対円錐の像、つまりカメラのキャリブレーションを見つけるのに役立つ情報は存在しません。しかし、カメラのキャリブレーションについて少しでも情報があれば、絶対円錐の位置を特定できる可能性があります。
例えば、画像シーケンスからシーンを再構成する際に使用される各カメラのキャリブレーションが同じであることが分かっているとします。これは、以下のことを意味します。各画像には座標系が定義されており、その座標系において、射影再構成を行うために使用した対応する特徴の画像座標を測定します。これらのすべての画像座標系において、IACは同じですが、それがどこに位置しているかは不明であるとします。この知識に基づいて、絶対円錐の位置を計算します。
絶対円錐曲線を見つける一つの方法は、1枚の画像におけるIACの位置を仮定することです。この仮定により、他の画像におけるIACの位置も同じになります。それぞれの円錐曲線を逆投影すると、空間上の円錐になります。3つの円錐がすべて1つの円錐曲線で交わる場合、それが絶対円錐曲線の位置の可能な解であり、再構成結果と整合するはずです。
これは概念的な説明に過ぎないことに注意してください。IACは当然のことながら複素点のみを含む円錐であり、その逆投影は複素円錐になります。しかし、代数的には、この問題はより扱いやすくなります。複雑ではありますが、IACは実二次形式(実対称行列で表される)で記述できます。逆投影された円錐も実二次形式で表されます。IACのある値に対して、逆投影された3つの円錐は空間内で円錐曲線で交わります。
通常、同じキャリブレーションを持つ3台のカメラがあれば、絶対円錐曲線を決定し、それによってカメラのキャリブレーションを決定することが可能です。しかし、これには様々な手法が提案されているものの、依然として非常に難しい問題です。
無限遠平面の把握。自動キャリブレーションの一つの方法は、まずそれが位置する平面を決定することから段階的に進めることである。これは、世界における無限遠平面を特定すること、ひいては世界のアフィン幾何学を決定することと等価である。第二段階として、平面上の絶対円錐の位置を特定し、空間のユークリッド幾何学を決定する。無限遠平面が分かっていると仮定すると、一連の画像のそれぞれから仮定されたIACを逆投影し、得られた円錐を無限遠平面と交差させることができる。IACが正しく選択されていれば、交差曲線が絶対円錐となる。したがって、各画像ペアから、逆投影された円錐が無限遠平面上の同じ円錐曲線で交わるという条件が得られる。これは、IACを表す行列の要素に線形制約を与えることがわかる。一連の線形方程式からIAC、ひいては絶対円錐を決定できる。したがって、無限遠面が特定されれば、自動キャリブレーションは比較的簡単です。しかし、無限遠面そのものを特定するのは、はるかに困難です。
画像内の正方形ピクセルを用いた自動キャリブレーション。カメラが部分的にキャリブレーションされている場合、投影再構成からキャリブレーションを完了することが可能です。カメラのキャリブレーションに関する非常に最小限の条件、つまりIACで表現される条件で十分です。興味深い例の1つは、カメラの正方形ピクセル制約です。これは、各画像においてユークリッド座標系が既知であることを意味します。この場合、無限遠平面にある絶対円錐は、画像平面の2つの円点で交わる必要があります。平面上の円点は、絶対円錐がその平面と交わる2つの点です。画像平面の円点を通る逆投影された光線は、絶対円錐と交差する必要があります。したがって、正方形ピクセルを持つ各画像から、絶対円錐と交わる2つの光線が決定されます。n枚の画像が与えられた場合、自動キャリブレーションのタスクは、空間内の2n本の光線と交わる空間円錐(絶対円錐)を決定するタスクになります。同等の幾何学的描像は、光線の集合を平面と交差させ、交点の集合が円錐曲線上にあることを求めることです。単純な数え上げの議論から、空間において8本の所定の光線と交わる円錐曲線は有限個しかないことがわかります。したがって、4枚の像から、可能性は有限個までではありますが、較正を決定できます。
ここまで、画像シーケンスからリアルなグラフィックスモデルを計算するために必要なすべての要素について説明しました。画像間の点の対応付けから、まず点集合の射影再構成を行い、選択した射影座標系におけるカメラの動きを決定することが可能です。
自動キャリブレーション技術を使用すると、画像シーケンスを撮影したカメラのキャリブレーションに一定の制約があると仮定すると、カメラをキャリブレーションし、その後、シーンを真のユークリッド構造に変換することができます。
シーンの射影構造が分かれば、画像のペアを関連付けるエピポーラ幾何学を見つけることが可能になり、これにより、更なる対応探索が直線に限定されます。つまり、一方の画像上の点は、もう一方の画像上の直線を定義し、その直線上に(まだ未知の)対応点が存在するはずです。実際、適切なシーンであれば、画像間の稠密な点のマッチングを実行し、撮影されたシーンの稠密な3Dモデルを作成することが可能です。これは三角形状の形状モデルの形をとり、その後、提供された画像からシェーディングまたはテクスチャマッピングされ、新しい視点を生成するために使用されます。このプロセスの手順は、図1.5と図1.6に示されています。

図1.5. (a) ベルギー、ルーヴェンの市庁舎の11枚の画像セットから抽出した3枚の高解像度画像(3000 × 2000ピクセル)。(b) 画像セットから計算されたユークリッド再構成画像の3つの視点。11台のカメラ位置と点群を表示。

図1.6. 稠密な再構成画像。これらは図1.5のカメラと画像から計算されたものです。(a) テクスチャなし、(b) テクスチャありのシーン全体の再構成画像。(c) テクスチャなし、(d) テクスチャありの (b) の白い四角形で囲まれた領域のクローズアップ画像。(e) テクスチャなし、(f) テクスチャありの (d) の白い四角形で囲まれた領域のクローズアップ画像。稠密な表面は、[Strecha-02] で説明されている3視点ステレオアルゴリズムを用いて計算されています。
この導入の最後に、コンピュータグラフィックスへの再構成手法のさらなる応用について述べます。自動再構成技術は、近年、映画業界では、実際のビデオシーケンスに人工的なグラフィックスオブジェクトを追加する手段として広く利用されるようになりました。カメラの動きをコンピュータで解析することで、これまで手動で行われていた人工的な挿入オブジェクトの位置合わせが簡素化されつつあります。
ビデオシーケンスに人工物体をリアルに挿入するための最も重要な要件は、カメラの正しい動きを計算することです。カメラの動きが正しく決定されなければ、背景ビデオと整合したグラフィックモデルの正しい視点シーケンスを生成することは不可能です。一般的に、ここで重要なのはカメラの動きだけです。シーンは既存のビデオに既に存在しているため、シーンを再構築する必要はありません。また、ビデオに映っているシーンの新しい視点も必要ありません。唯一の要件は、グラフィックモデルの正しい透視視点を生成できることです。
ユークリッド座標系におけるカメラの動きを計算することが不可欠です。カメラの射影運動を知るだけでは不十分です。これは、シーンにユークリッド物体を配置する必要があるためです。このグラフィックスオブジェクトとカメラが同じ座標系で認識されていない場合、挿入されたオブジェクトの生成された視点は、既存のビデオで見られるシーンの構造に対して歪んで見えることになります。
カメラの正しい動きとキャリブレーションが分かれば、挿入されたオブジェクトをシーンにリアルにレンダリングできます。フレームごとのカメラキャリブレーションの変化が正しく判断されれば、シーケンス中にカメラの焦点距離(ズーム)を変更できます。クロップによって、シーケンス中に主点が変化することさえ可能です。
レンダリングされたモデルをビデオに挿入する際、モデルが既存のシーン全体の前面に配置されていれば、作業は比較的簡単です。そうでない場合、シーンによってモデルの一部が隠れてしまうオクルージョンが発生する可能性があります。ビデオ拡張の例を図1.7に示します。

図1.7. 拡張ビデオ。アニメーション化されたロボットがシーンに挿入され、図1.3の計算されたカメラを使用してレンダリングされます。(a)-(c) シーケンスの元のフレーム。(d)-(f) 拡張されたフレーム。図は2d3 (www.2d3.com) の提供です。