図を見ればわかること

なにものか？

図を眺めているだけで答えの正しさを確信してしまうものを集めてみる。

・"mathematics without words"
・"proofs without words"
を検索して画像を選択すると同じようなものがたくさん見つかった･･･

●\(\displaystyle\sum_{n=1}^\infty \left(\frac{1}{2}\right)^n = \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots=1\)

● \(\displaystyle\sum_{n=1}^\infty \left(\frac{1}{3}\right)^n = \frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\cdots=\frac{1}{2}\)

● \(\displaystyle\sum_{n=1}^\infty \left(\frac{1}{4}\right)^n = \frac{1}{4}+\frac{1}{16}+\frac{1}{64}+\cdots=\frac{1}{3}\)

● \(\displaystyle\sum_{n=1}^\infty \left(\frac{1}{m}\right)^n = \frac{1}{m}+\left(\frac{1}{m}\right)^2+\left(\frac{1}{m}\right)^3+\cdots=\frac{1}{m-1}\)

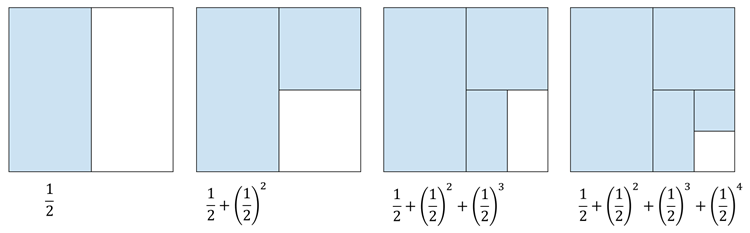
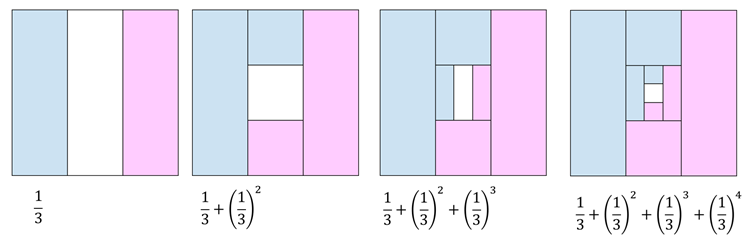
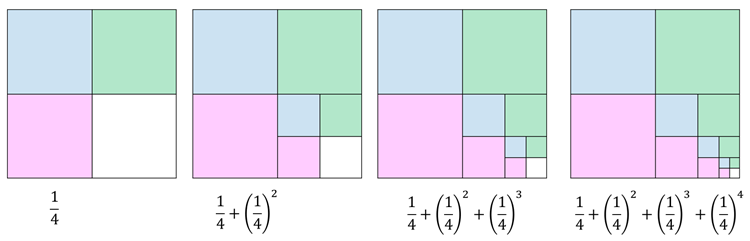
・1 を \(m\) 等分し \(\left(=\frac{1}{m}\right)\), \(m-1\) 人に分配
・残りを \(m\) 等分し \(\left(=\left(\frac{1}{m}\right)^2\right)\), \(m-1\) 人に分配
・残りを \(m\) 等分し \(\left(=\left(\frac{1}{m}\right)^3\right)\), \(m-1\) 人に分配
　\(\vdots\)

・1 が \(m-1\) 人に等分配される

※ 代数的には等比級数の公式を使えば機械的に求められるが･･･ \[ \sum_{n=1}^\infty \left(\frac{1}{m}\right)^n=\frac{\frac{1}{m}}{1-\frac{1}{m}}=\frac{1}{m-1} \]

● 四角数 \(\displaystyle\sum_{n=1}^m (2n-1)=m^2\)

● \((a+b)\times(c+d)=ac+ad+bc+bd\)

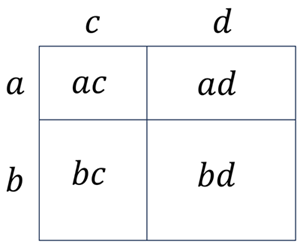
代数的には \((c+d)=X\) と置いて分配法則を適用 \[ (a+b)\times X = aX+bX \] \(X\) を元に戻して、分配法則を適用 \[ aX+bX = a(c+d)+b(c+d)=ac+ad+bc+bd \]

● ピタゴラスの定理

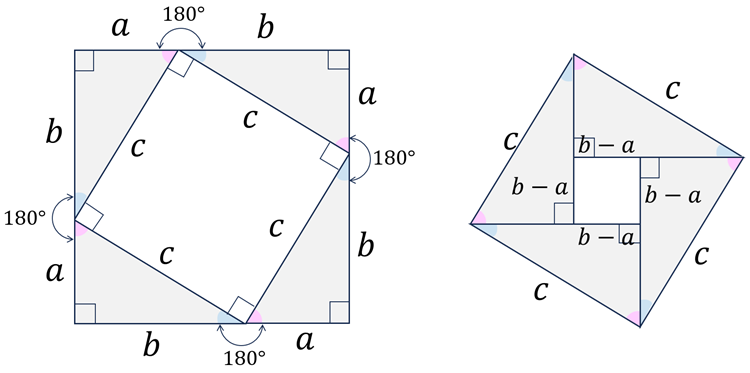
図と代数のハイブリッドで理解するパターン。

・図(左) \[ \begin{align} (a+b)^2 - c^2 &= \frac{1}{2}ab \times 4 = 2ab \\ \\ a^2+b^2+\cancel{2ab} - c^2 &= \cancel{2ab} \\ \\ a^2+b^2 &= c^2 \end{align} \] ・図(右) \[ \begin{align} c^2 - (b-a)^2 &= \frac{1}{2}ab \times 4 = 2ab \\ \\ c^2 - (b^2 + a^2 - \cancel{2ab}) &= \cancel{2ab} \\ \\ c^2 &= b^2 + a^2 \end{align} \] 図だけで理解してみる。

● A(十分条件) ⇒ B(必要条件)

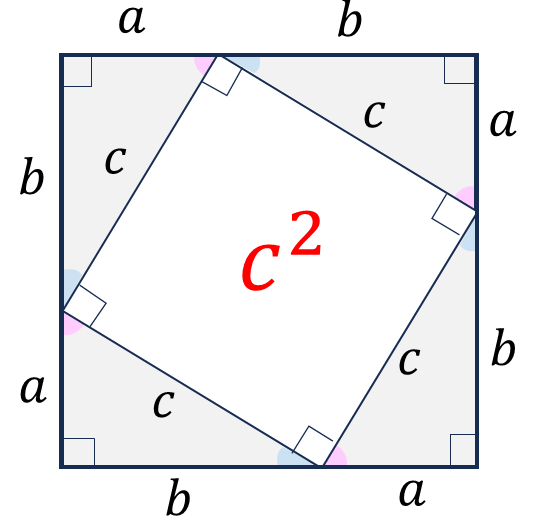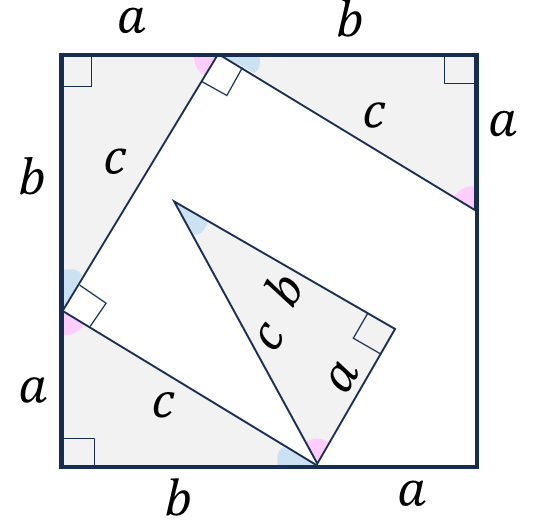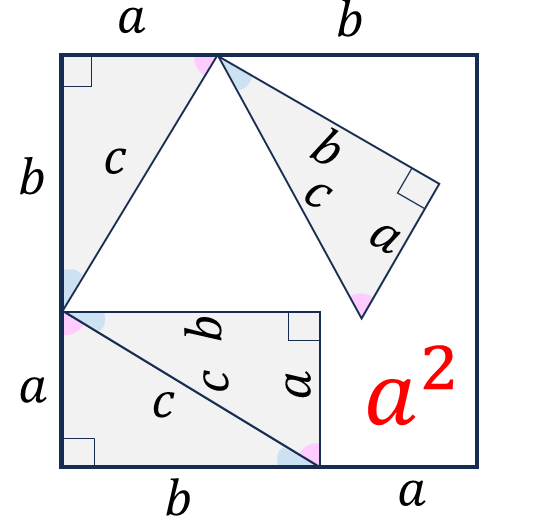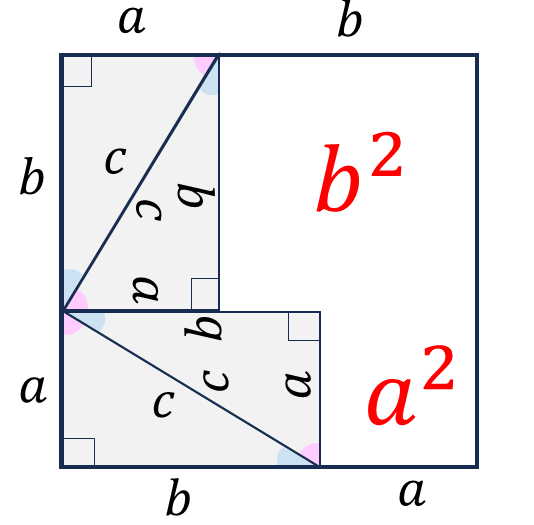
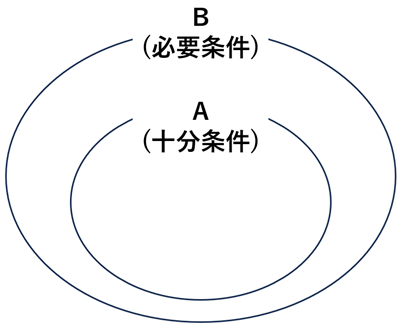
・ベン図にすると必要条件と十分条件の関係が明確になる。
・演繹(A⇒B) は
　- マチガイのない推論であること
　- でも, 新しいことは何も生み出さないこと(話が狭くなるダケ)
　であることがわかる。

● 面積図

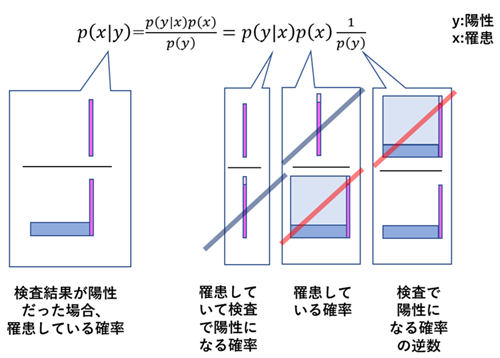
ことばでゴチャゴチャいわれると複雑に感じるが, 面積図で表すと状況がわかりやすくなる(気がする)。

・日本人の2%が罹患しているある病気について考えます。
・この病気の検査方法では、実際に病気に罹患している人が陽性と判定される確率が95%、
　逆に罹患していない人が陰性と判定される確率は90%であると言われています。
・ある人がこの病気の検査を受けて陽性という判定を受けた時、
　本当にこの病気に罹患している確率はいくらでしょうか。

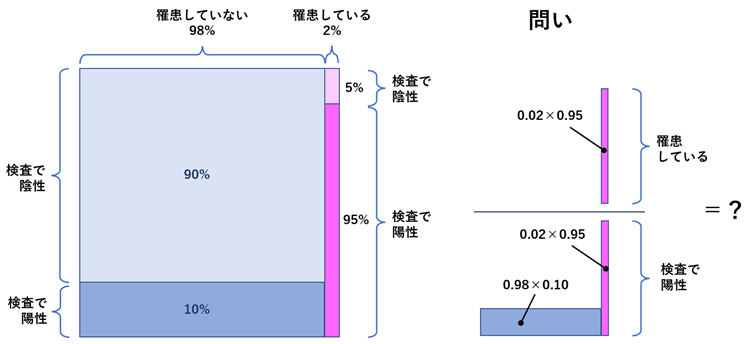
ベイズの式と面積図の関係はこんな感じ。

● 相加平均 ≧ 相乗平均

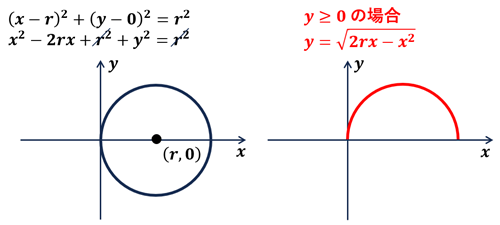
・準備①

点 \((r,0)\) との距離が \(r\) の点の集合：\((x,y)\)

・準備②

変数変換 \(\displaystyle r→\frac{a+b}{2},　x→a\)

　　\(\displaystyle y=\sqrt{2rx-x^2}=\sqrt{2\frac{a+b}{2}a-a^2}=\sqrt{a^2+ab-a^2}=\sqrt{ab}\)

変数変換 \(\displaystyle r→\frac{a+b}{2},　x→\frac{a+b}{2}\)

　　\(\displaystyle y=\sqrt{2rx-x^2}=\sqrt{2\frac{a+b}{2}\frac{a+b}{2}-\left(\frac{a+b}{2}\right)^2}=\sqrt{\left(\frac{a+b}{2}\right)^2}=\frac{a+b}{2}\)

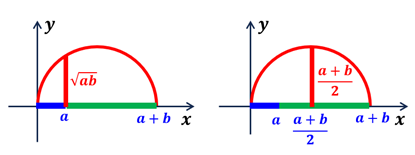
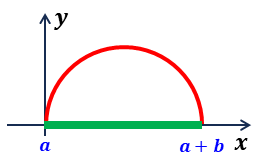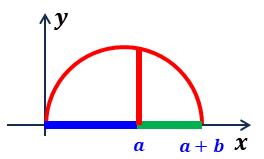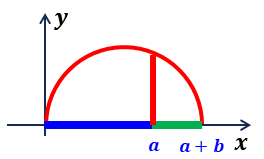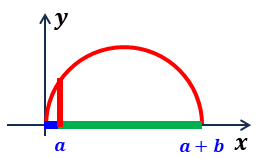
データ \(a\) とデータ \(b\) を \(x\) 軸上に並べ, \(\displaystyle x=\frac{a+b}{2}\) を中心に半円を描くと,

・\(x=a\) の位置の半円の高さ \(y=\) 相乗平均

・\(\displaystyle x=\frac{a+b}{2}\) の位置の半円の高さ \(y=\) 相加平均

となる。

・相加平均と相乗平均

データ \(a\) とデータ \(b\) の比率を変えて相乗平均を変えても, 相加平均を超えないことが判る。

● \(A\sin(ωt)+B\cos(ωt)\)

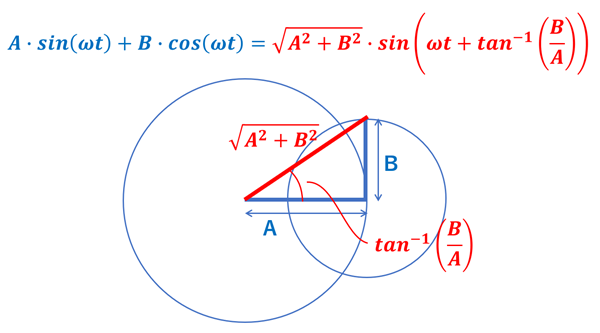
・\(\sin\) は初期位相 0°の円運動の射影
・\(\cos\) は初期位相 90°の円運動の射影
　同じ周波数の \(\sin\) と \(\cos\) を足したらどうなるか?

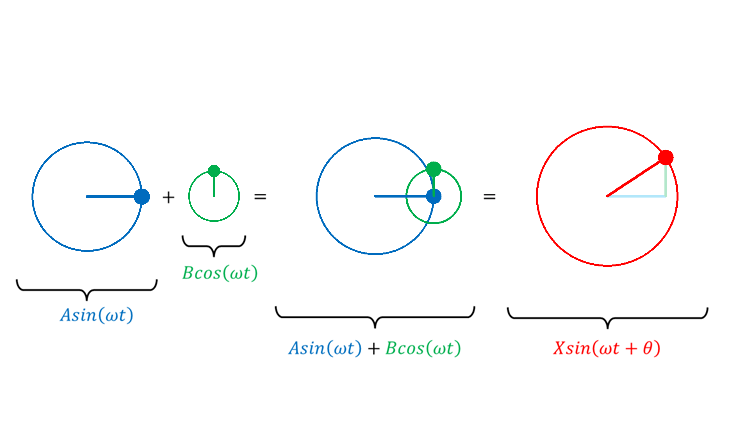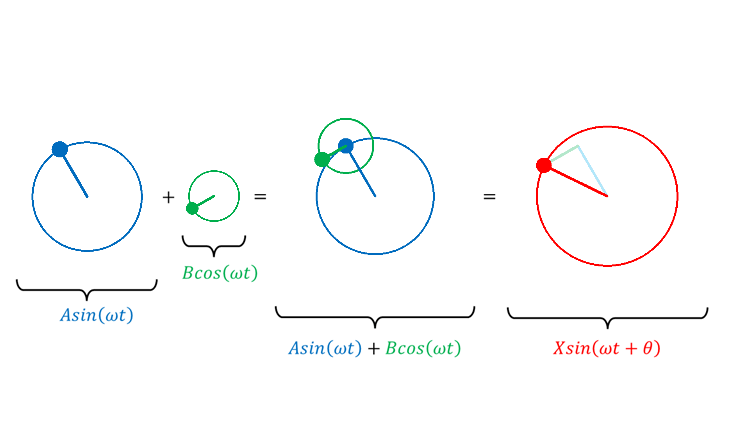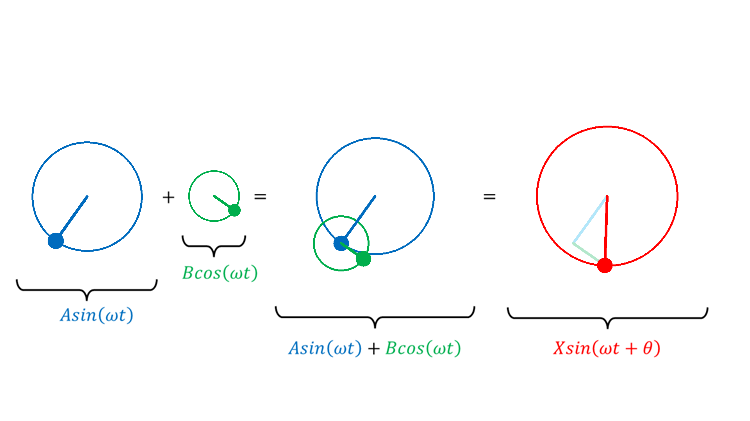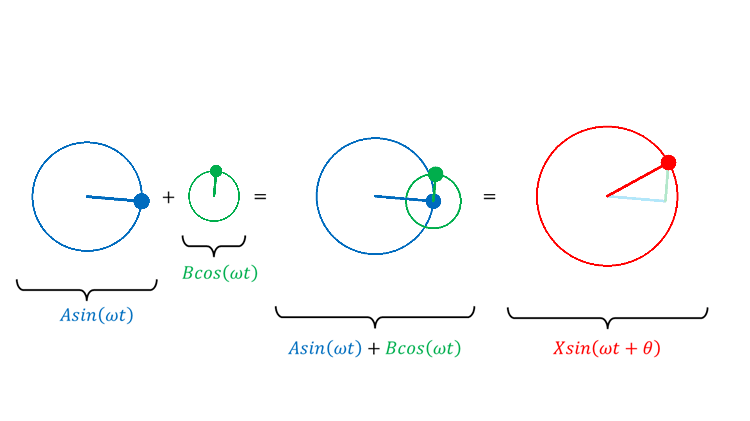
初期位相が 0°でも 90°でもない, 奇関数でも偶関数でもないありふれた三角関数になる。