生物学的脳は複雑な神経活動を示し、ニューロン間のタイミングと相互作用は脳の情報処理において極めて重要です。ほとんどの深層学習アーキテクチャは、時間的ダイナミクスを抽象化することで神経活動を単純化しています。本稿では、このパラダイムに挑戦します。ニューロンレベルの処理と同期を組み込むことで、神経タイミングを基礎要素として効果的に再導入することができます。本稿では、ニューロンダイナミクスを中核表現として活用するように設計されたモデル、Continuous Thought Machine (CTM) を紹介します。CTMには2つの中核的な革新があります。(1) ニューロンレベルの時間的処理(各ニューロンが固有の重みパラメータを使用して入力信号の履歴を処理する)、(2) 潜在表現として用いられるニューロン同期です。CTMは、計算効率を向上させる過度に単純化されたニューロン抽象化と生物学的リアリズムのバランスをとることを目指しています。 CTMは、深層学習に適した計算処理能力を維持しながら、本質的な時間的ダイナミクスを効果的に捉える抽象化レベルで動作します。ImageNet-1K分類、2次元迷路解法、ソーティング、パリティ計算、質問応答、強化学習タスクなど、様々な難解タスクにおいて、CTMの優れた性能と汎用性を実証しました。CTMは、豊富な内部表現の表示と内部プロセスによる自然な解釈の道筋の提供に加え、複雑な逐次推論を必要とするタスクも実行できます。CTMは適応型コンピューティングも活用でき、単純なタスクでは早期に停止し、より困難なインスタンスに直面しても計算を継続できます。本研究の目的は、最先端の新しい成果を追求することではなく、CTMとそれに関連するイノベーションを共有することです。そのため、CTMは、より生物学的に妥当で強力な人工知能システムの開発に向けた重要な一歩となると考えています。
本レポートと併せて、モデルのチェックポイントを含むCTMコードリポジトリを公開しました。また、CTMの機能を最大限に引き出すインタラクティブなデモをご覧いただくために、プロジェクトページもぜひご覧ください。
ニューラルネットワーク(NN)はもともと生物の脳に着想を得たものですが、生物学的な脳とは大きく異なる性質を保っています。脳は時間とともに進化する複雑な神経ダイナミクスを示しますが、現代のNNは大規模な深層学習を容易にするために、そのような時間的ダイナミクスを意図的に抽象化しています。例えば、標準的なNNの活性化関数は、ニューロンの発火率を意図的に抽象化し、生物学的プロセスの時間的ダイナミクスを単一の静的な値に置き換えたものと見ることができます。このような単純化は、大規模機械学習の大きな進歩を可能にしましたが(Goodfellow et al., 2016; LeCun et al., 2015; Wei et al., 2022)、生物学的ニューラルコンピューティングを支配する基本原理からの逸脱をもたらしました。
数億年にわたる進化は、生物の脳にスパイクタイミング依存可塑性(STDP)(Caporale and Dan, 2008)やニューロン振動といった豊かな神経ダイナミクスを与えてきました。これらのメカニズム、特にスパイクタイミングと同期に固有の時間的コーディングを模倣することは、大きな課題となります。その結果、現代のニューラルネットワークは、計算を実行するために時間的ダイナミクスに依存せず、むしろ単純さと計算効率を優先しています。この抽象化は、特定のタスクのパフォーマンスを向上させる一方で、人間の認知の柔軟で一般的な性質と現在のAI機能との間に認識されているギャップの一因となっており、時間的処理に関連する可能性のある基本的な要素が現在のモデルに欠けていることを示唆しています(Chollet, 2019; Lake et al., 2017; Marcus, 2018)。
なぜこの研究を行うのか? 実際、多くの実用分野における現代のAIの目覚ましい高性能は、ニューラルダイナミクスのエミュレーションが不当であること、あるいは知能の時間的側面を明示的に考慮することが非実用的であることを示唆しています。しかしながら、人間の知能は非常に柔軟で、データ効率が高く、未知の状況にもうまく外挿できる流動性を備えており、学習と適応が時間の矢に結びついたオープンワールドに存在します。したがって、人間の知能には常識、オントロジー推論を活用する能力、透明性/説明可能性、そして強力な一般化が含まれます。AIはまだこれらの特性を説得力を持って示していません(Chollet, 2019; Hohenecker and Lukasiewicz, 2020; Marcus, 2018; Thompson et al., 2020)。
これらの理由から、我々は、人工知能が最終的に人間の脳に匹敵する、あるいは凌駕するレベルの能力を達成するためには、時間がその中心的な要素となるべきだと主張する(Cariani and Baker, 2022; Maass, 2001)。したがって、本研究では、神経活動を知性の中心的な側面として見落とすことによって生じる大きな制約に対処する。我々は、神経タイミングを基礎要素として明示的に組み込むように設計された、新しいニューラルネットワークアーキテクチャである連続思考マシン(CTM)を導入する。我々の貢献は以下の通りである。
推論モデルと再帰性。人工知能の最先端は重大な岐路に立たされています。それは、単純な入出力マッピングを超えて、真の推論能力へと移行することです。既存モデルのスケーリングは目覚ましい進歩をもたらしましたが、それに伴う計算コストとデータ需要は持続不可能であり、このアプローチの長期的な実行可能性に疑問が生じています。シーケンシャルデータの場合、長年用いられてきた再帰型アーキテクチャ(Dey and Salem, 2017; Hochreiter and Schmidhuber, 1997; Medsker and Jain, 1999)は、主にトランスフォーマーベースのアプローチ(Vaswani et al., 2017)に取って代わられました。しかしながら、再帰性はモデルの複雑性を拡張するための自然な手段として再び浮上しています。再帰性は、反復処理と時間の経過に伴う情報の蓄積を可能にするため、有望です。現代のテキスト生成モデルでは、中間世代を、テスト時に追加の計算を可能にする再帰的な形式として用いています。最近、他の研究によって、潜在層の再帰的適用の利点が実証されています (Geiping et al., 2025; Jaegle et al., 2021; Yang et al., 2023)。
これらの手法は生物学的脳の再帰構造に近づく一方で、根本的なギャップが依然として残っています。再帰は不可欠ではあるものの、パズルの一部に過ぎないと私たちは考えています。再帰によって解き明かされる時間的ダイナミクス、つまり神経活動の正確なタイミングと相互作用も同様に重要です。CTMは既存のアプローチと3つの点で異なります。(1) 内部の「思考」次元により、考えられるあらゆるデータモダリティにおける逐次的な思考が可能になります。(2) プライベートなニューロンレベルのモデルにより、正確な神経タイミングを考慮することができます。(3) 神経同期を、タスク解決のための表現として直接使用できます。
有用な副作用 CTMの内部的な再帰性は思考に類似しており(そのため、この名称が付けられました)、より単純なタスク(例えば、識別しやすい画像、図5参照)では「思考」を早期に停止し、より困難なタスク(例えば、長い迷路、セクション4.3参照)ではより深く思考することで、ある種の適応型計算を可能にします。特に、CTMは、調整が困難な追加の損失を必要とせずに、一種の適応型計算を実現します(Graves, 2016)。実際、解釈可能で直感的な問題解決戦略の出現が観察されており、ニューラルタイミングを活用することで、より多くの新たなメリットと、潜在的により効果的なAIシステムにつながる可能性があることを示唆しています。神経タイミングを明示的に設定することのもう一つのプラス効果は、情報をこのタイミング内に符号化できることです。その結果、文脈化能力が向上します。私たちはこれを検証するために2D迷路解法チャレンジを設計しました(セクション4)。
本論文の残りの部分は以下のように構成されています。第2節ではCTMの技術的詳細を説明します。第3節から第10節では、CTMを画像分類、2次元迷路、ソート、パリティ、質問応答、そして単純な強化学習タスクに適用します。各実験は特定の特性を調査するように設計されており、可能な限りベースラインと比較します。第12節では、得られた知見を考察し、今後の研究の方向性を示します。第13節では最終的な結論を導き出します。CTMを通して神経タイミングを明示的にモデル化することで、より生物学的に妥当で高性能な人工知能システムへの道を切り開くことを目指します。
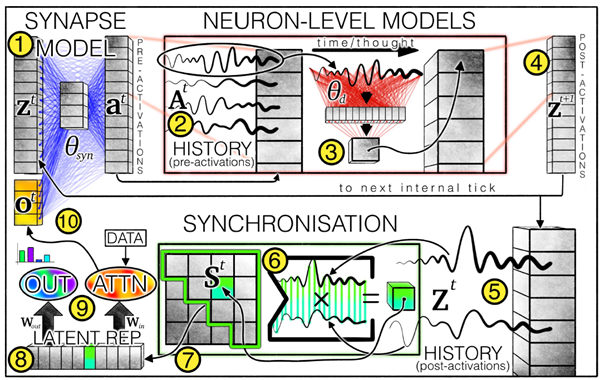
連続思考マシン(CTM)は、データ思考への新たなアプローチを可能にするニューラルネットワークアーキテクチャです。従来のフィードフォワードモデルとは異なり、ニューラルダイナミクスの概念を機能の中核要素として明示的に組み込んでいます。図1はCTMの概要を示しており、番号1から番号9はフローを示しています。リスト1は、分かりやすくするために簡略化された概要リストを示しています。図1の黄色の番号は、本稿の残りの部分で参照されます。

図1 | CTMアーキテクチャの概要。シナプスモデル(重みは青線で示される、式1)は、ニューロン間の相互作用をモデル化し、事前活性化を生成します。各ニューロンについて、事前活性化の履歴が保持され(式2)、その最新の履歴がニューロンレベルモデル(重みは赤線で示される、式3)によって事後活性化の生成に使用されます。事後活性化の履歴も保持され(式4)、同期行列(式5および式10)を計算するために使用されます。同期行列からニューロンペアが選択(セクション2.4.1を参照)され、CTMが出力(式6)を生成し、相互注意(式7および式8)を通じてデータを変調するための潜在表現が生成されます。変調されたデータ(例えば、注意出力)は、次の内部ティックのポストアクティベーションと連結されます。
他の再帰型アーキテクチャ(RNNなど)は、データとは別の内部時間次元を組み込むように設定できます(Graves, 2016; Kirsch and Schmidhuber, 2021; Kirsch et al., 2022; Pedersen et al., 2024; Schwarzschild et al., 2021)が、CTMは2つの重要な点で異なります。(1)従来の活性化関数を使用する代わりに、CTMはそれぞれ独自の重みを持つニューロンレベルのモデルを事前活性化の履歴に適用して、複雑なニューロンレベルの活動を生成します(例についてはセクション3を参照)。(2)CTMは、データを変調して出力を生成する際に、ニューラルネットワークの同期を潜在表現として直接使用します(セクション2.4を参照)。これにより、ニューロンの正確なタイミングと相互作用を作成、維持、活用する新しいレベルの能力が効果的に実現されます。以下のサブセクションでは、CTMについて詳しく説明します。
# 定義 ( 簡潔にするためにハイパーパラメータは示していない )
# バックボーンとしては、例えば画像用の ResNet などが考えられる。
backbone = FeatureEncoder ()
# Q, KVプロジェクター、および標準アテンションモジュール
q_projector , kv_projector = Linear (), Linear ()
attn = MultiHeadAttention ()
# シナプスモデルは線形、MLP、U-NETのいずれか
synapses = MLP ()
# ニューロンレベルモデル(リスト2参照)
neuron_level_models = NLMS ()
# 同期からの出力プロジェクター(リスト3を参照)
output_proj = Linear ()
# 事前活性化とZを学習可能なパラメータとして初期化する
# Dはモデルの幅
z_init = Parameter ( size =(D))
# Mはニューロンの記憶長
pre_acts_history_init = Parameter ( size =(D, M))
# MODEL LOGIC
# バックボーンを使用して入力を特徴付け、KVトークンを計算する
kv = kv_projector ( backbone ( inputs ))
# 各ミニバッチで、学習可能なpre_act_historyを初期化する
pre_acts_history = pre_acts_history_init . unsqueeze (0). repeat (B, dim =0) # (B, D, M)
# そして、学習可能なz_initでpost_acts_historyを開始する
post_acts_history = [ z_init . unsqueeze (0). repeat (B, dim =0)]
outputs_history = []
# クエリデータの初期アクション同期を取得する
synch_a = compute_synch ( post_acts_history , type =" action ")
# その他の初期化(学習可能な開始履歴と最初の事前attn roundを含む)
for step in range ( n_thought_steps ):
# Project attention query の同期をオフにする
q = q_projector ( synch_a )
attn_out = attn (q, kv , kv)
# アテンションの出力を連結し、シナプスを介して処理する
pre_acts = synapses ( concat (( attn_out , z )))
# 事前アクティベーションの履歴を保存する。これはFIFO構造
pre_acts_history = concat (( pre_acts_history [:, :, : -1] , pre_acts ), dim = -1)
# 履歴を使用してポストアクティベーションを計算する(リスト2を参照)
z = neuron_level_models ( pre_acts_history )
post_acts_history . append (z)
# 同期を計算する(リスト3を参照)
synch_a = compute_synch ( post_acts_history , type =" action ")
synch_o = compute_synch ( post_acts_history , type =" output ")
# プロジェクト予測/出力オフ同期
outputs_history . append ( output_proj ( synch_o ))
# 損失関数の思考ステップごとの出力を返す
return outputs_history
リスト1 | CTMコードの簡略化された概要。特徴はバックボーン(画像の場合はResNetレイヤーなど)を用いてエンコードされ、データはニューラルネットワークの同期からクエリを投影することで処理されます。情報はMLPシナプスモデルを用いてニューロン間で共有され、事前活性化が生成されます。追跡された事前活性化の履歴にプライベートニューロンレベルモデルが適用されます(リスト2を参照)。同期は追跡された事後活性化の履歴から計算されます(リスト3を参照)。そして、出力は同期から投影されます。すべてのコードはここから入手できます。
まず、認知が生じ得る内部次元 \(𝑡∈{1, . . . , 𝑇}\) を導入する。この内部次元の1つのステップは、図1から図2への流れとして示される。この次元はデータとは分離されており、内部的に展開され、どのデータ次元にも結び付けられていない。内部次元に沿った再帰性は決して新しい概念ではない(Chahine et al., 2023; Geiping et al., 2025; Jaeger, 2007)。近年、現代のAIに推論機能を組み込もうとする動きが高まっているため、この概念はますます注目を集めている。 RNNやTransformerといった従来のシーケンシャルモデルとは異なり、CTMはデータに内在するシーケンス(例えば、文中の単語や動画のフレーム)に従って入力を段階的に処理しますが、CTMは内部の「思考ステップ」という自己生成タイムラインに沿って動作します。この内部展開により、画像や迷路といった静的または非シーケンシャルなデータを処理する場合でも、モデルは反復的に表現を構築し、改良することができます。その結果、CTMは外部タイミングから切り離された思考プロセスを行うことができ、より柔軟で解釈しやすく、生物学に着想を得た計算が可能になります。関連研究(Kirsch and Schmidhuber, 2021; Kirsch et al., 2022; Pedersen et al., 2024; Schwarzschild et al., 2021)で使用されている既存の命名法に従い、以降はこれらの思考ステップを「内部ティック」と呼びます。 CTMの内部次元は、神経活動のダイナミクスが展開される領域です。私たちは、このようなダイナミクスが知的思考の礎となる可能性が高いと考えています。リスト1のforループは、図1に示したプロセスを表現しています。
①シナプスモデル \(𝑓_{𝜃_{syn}}\) は、共有𝐷次元潜在空間 \(z^𝑡 ∈ \mathbb ℝ^𝐷\) のニューロンを相互接続します。 ここで、𝑡 はCTMの再帰的展開における現在の内部ティックです。𝜃syn は再帰的シナプスモデルの重みです。シナプスモデルは、標準的な活性化関数が続く単一の線形投影としてパラメータ化することも、多層パーセプトロン (MLP) としてパラメータ化することもできます。実験的に、U-NET風 (Ronneberger et al., 2015) MLPアーキテクチャがすべてのタスクでより優れたパフォーマンスを発揮することがわかりました (シナプスモデルの詳細については付録B.1を参照)。これは、シナプス接続が追加のより深い計算から恩恵を受けることを示しています。シナプスモデルを適用すると、内部ティック \(𝑡\) における事前活性化と考えられるものが生成されます。 \[ a^𝑡 = 𝑓_{𝜃_{syn}} (concat(z^𝑡 , o^𝑡)) ∈ \mathbb ℝ^𝐷 \tag{1} \] ここで、\(o^𝑡\)は入力データ(直接またはアテンションの出力として。式8を参照)からのものであり、2.4節で説明します。
最新のM個の事前アクティベーションは、事前アクティベーションの「履歴」②に収集されます。 \[ A^𝑡 = [a^{𝑡−𝑀+1}\; a^{𝑡−𝑀+2}\;\cdots a^𝑡 ]∈ \mathbb ℝ^{𝐷×𝑀} \tag{2} \] 履歴の最初の \(𝑀\) 要素と最初の \(z^{𝑡=1}\) を初期化する必要があります。当初はこれらの2つのゼロを初期化する実験を行いました(RNNでも同様の戦略が採用されています)。しかし、これらのパラメータを学習可能にすることが最適であることがわかりました。
# Initialisations
weights_1 = Parameter ( shape =(M, d_hidden , d_model ))
bias_1 = zeros ( shape =(1 , d_hidden , d_model ))
weights_2 = Parameter ( shape ( d_hidden , d_model ))
bias_2 = zeros ( shape =(1 , d_model ))
# Forward pass
# b=batch , M= memory , d= d_model , h= d_hidden
# inputs are shape (b, d, M)
inputs = pre_acts_history [-M:]
out = einsum ('bdM ,Mhd -> bdh ', inputs , weights_1 ) + bias_1
out = einsum ('bdh ,hd ->bd ', out , weights_2 ) + bias_2
リスト 2 | ニューロンレベルモデル:③。einsum を使用すると、ニューロンレベルモデルの適用が大幅に簡素化され、高速化されます。出力を並列に計算できるためです。最初の einsum は、入力履歴(最新の 𝑀 に切り捨てられた)から各ニューロンの h 次元潜在変数を計算します(②)。次に、2 番目の einsum は、ニューロンごとの単一の活性化を計算します(ここでは簡潔にするために「1」次元は無視します)。
𝑀は、各ニューロンレベルモデルが扱う事前活性化の履歴の長さを実質的に定義します。𝑀の値の範囲をテストした結果、10~100の範囲が効果的であることがわかりました。各ニューロン \(\{1, . . . , 𝐷\}\) には、それぞれ独自の③プライベートパラメータ化モデルが与えられ、このモデルは、我々が④事後活性化と呼ぶものを生成します。 \[ z_d^{𝑡+1} = 𝑔_{𝜃_𝑑} (A_d^𝑡) \tag{3} \] ここで、\(𝜃_𝑑\) はニューロン \(𝑑\) の一意のパラメータであり、\(z_d^{𝑡+1}\) はベクトル内の全ての事後活性化を含む単一のユニットです。幅 𝑑hidden の単一の隠れ層を持つ MLP を使用します。\(A_d^𝑡\) は \(𝑀\) 次元ベクトル(時系列)です。ニューロンに独自の内部モデルを持たせるには、追加のパラメータが必要となり、\(𝐷 × (𝑀 × 𝐻_{𝑑𝑖𝑚} + 𝐻_{𝑑𝑖𝑚})\) のようにスケーリングされます(ここで、\(𝐻_{𝑑𝑖𝑚}\) はニューロンレベルのMLPの幅であり、単純化のためバイアスパラメータは無視します)。しかし、この追加のパラメータコストにより、モデリングの自由度が高まります。
ニューロンの事後活性化の全セットは、アテンション出力(セクション2.4を参照)と連結され、\(𝑓_{𝜃_1}\)に再帰的に入力され、展開される思考プロセスにおける次のステップ(\(𝑡 +1\))の事前活性化を生成します。 CTMが採用する再帰的思考プロセスは、リスト1と2に示されています。ここでは、CTMが同期を通じてデータ(入力と出力の両方)とどのように相互作用するかについて説明します。
# AT INITIALISATION :
# Pre choose D_chosen neuron pairs from D total neurons
# D_chosen can be D_out or D_action
# Other neuron selection strategies exist , but here we show random selection
idxs_left = randint (low =0, high =D, size = D_chosen )
idxs_right = randint ( low =0, high =D, size = D_chosen ) # can overlap
# Define learnable exponential decay scaling factors per neuron pair
r = Parameter ( zeros (1, D_chosen , 1))
# INITIALISATION OVER .
# IN FORWARD PASS :
S = stack ( post_acts_history , 1) # S is of shape [B, T= history length ]
# decay BACK in time
t_back = range (T -1, -1, -1). reshape (1, T, 1)
# Compute per NEURON PAIR exponential decays , and expand over D_chosen
exp_decay = exp(- t_back * r). expand (1, T, D_chosen )
# Compute weighted inner dot products using differet subsets of neurons
S_multiplied = S[: ,: , idxs_left ] * exp_decay * S[: ,:, idxs_right ] # [B, T, D_chosen ]
# Sum over the free T dimension and normalise by sqrt of AUC of decays
synch_representation = ( S_multiplied ). sum (1)/ sqrt ( exp_decay . sum (1)) # [B, D_chosen ]
リスト3 | リスト1で使用した潜在表現を作成するためのニューラル同期。慎重な再形成とブロードキャストにより、ニューロンペアごとに学習可能な指数関数的減衰を同期に使用できるようになり、CTMは複雑なタイミング依存性を学習できます。減衰パラメータはゼロ(つまり減衰なし)に初期化されます。このプロセスは出力とアクションに対して繰り返されます(セクション2.4.1を参照)。実際には、計算オーバーヘッドを大幅に削減する再帰的なアプローチを使用します。付録Kを参照してください。
CTMは外界とどのように相互作用するべきでしょうか?具体的には、CTMはどのように入力を消費し、出力を生成するべきでしょうか?私たちは、思考に似た何かが展開できるタイミングの次元を導入しました。また、CTMとデータとの関係(いわば相互作用)は、ニューロンの状態(ある時点)のスナップショットではなく、ニューロン活動の進行中の時間的ダイナミクスに依存するようにしたいと考えています。1 解決策として、私たちは再び自然の脳に着目し、神経同期の概念(Uhlhaas et al., 2009)が適切かつ強力であることを見出しました。同期を実現するために、私たちはまず、活性化後の活動を活性化後の「履歴」に収集することから始めます。
1 私たちはスナップショット表現から始めましたが、ニューロンの振動的な挙動が現れたため、安定した挙動を得るのに苦労しました。
\[ \mathbf Z^𝑡 =[z^1\; z^2\;· · ·\; z^𝑡] ∈ \mathbb ℝ^{𝐷×𝑡} \tag{4} \] \(\mathbf Z^𝑡\) の長さは現在の内部ティックに等しいため、この次元は固定されておらず、任意の大きさになり得る。神経同期は、活性化後の履歴間の内部ドット積によって生成される行列として定義される。 \[ \mathbf S^𝑡 = \mathbf Z^𝑡 · (\mathbf Z^𝑡)^⊺ ∈ \mathbb ℝ^{𝐷×𝐷} \tag{5} \]
この行列は \(\mathcal O(D^2)\) でスケールするため、ニューロン \(𝑖\) と \(𝑗\) 間の同期を捉える \((𝑖, 𝑗)\) 行列ペアをサブサンプリングするのが実際的です。これを行うには、\(\mathbf S\) から \(𝐷_{out}\) と \(𝐷_{action} (𝑖, 𝑗)\) のペアをランダムに選択し、2 つの同期表現 \(\mathbf S_{out}^𝑡 ∈ \mathbb ℝ^{𝐷_{out}}\) と \(\mathbf S_{action}^𝑡 ∈ \mathbb ℝ^{𝐷_{action}}\) を収集します。 \(\mathbf S_{out}^𝑡\) は次のように出力空間に投影できます。 \[ \mathbf y^𝑡 = \mathbf W_{out} · \mathbf S_{out}^𝑡 \tag{6} \] そして、\(\mathbf S_{action}^𝑡\) は世界に対してアクションを起こすために使われる(例えば、我々の設定では注意を介して)。 \[ \mathbf q^𝑡 = \mathbf W_{in} · \mathbf S_{action}^𝑡 \tag{7} \] ここで、\(\mathbf W_{out}\) と \(\mathbf W_{in}\) は学習済みの重み行列であり、同期を観測用ベクトル(例:注意クエリ、\(\mathbf q^𝑡\))または出力用ベクトル(例:ロジット、\(\mathbf y^𝑡\))に投影する。\(\mathbf S^𝑡、𝐷_{out}\) と \(𝐷_{action}\) には \((𝐷 × (𝐷 + 1))/2\) 個の一意のペアリングが存在するが、この値よりも桁違いに小さくなる可能性がある。とはいえ、完全な同期行列は大きな表現であり、将来的に大きな可能性を秘めている。 ほとんどの実験では、標準的なクロスアテンション(Vaswani et al., 2017)を使用した。 \[ \mathbf o^𝑡 = Attention(𝑄 = \mathbf q^𝑡 , 𝐾𝑉 = FeatureExtractor(data)) \tag{8} \] ここで、まずResNet (He et al., 2016)などの「FeatureExtractor」モデルを用いて、キーと値の有用な局所特徴を構築します。\(\mathbf o^𝑡 ∈ \mathbb ℝ^{𝑑_{input}}\) は、\(𝑛_{heads}\) ヘッドを用いたアテンションの出力であり、次の繰り返しサイクルのために \(\mathbf z^{𝑡+1}\) と連結されます。わかりやすくするために、リスト3に、学習可能な時間的依存性のスケーリング(下記参照)を含め、このプロセスがコードでどのように見えるかを示します。
時間依存性のスケーリング \(\mathbf S^𝑡\) はステップ \(𝑡\) までのすべての内部ティックからの情報を集約するため、後のステップは同期への影響が減少する可能性があります。CTMに過去の活動の影響を調整する柔軟性を提供するために、学習可能な指数関数的に減少する再スケーリング係数を導入します。各ニューロンペア\(𝑖𝑗\)に対して学習可能なスケーリング係数\(𝑟_{𝑖𝑗} ≥ 0\)が与えられた場合、\(𝑡\) にわたる再スケーリング係数は次のように計算されます。 \[ \mathbf R_{ij}^𝑡 =[\exp(−𝑟_{𝑖 𝑗} (𝑡 − 1))\; \exp(−𝑟_{𝑖 𝑗} (𝑡 − 2))\; · · ·\; \exp (0)]^T ∈ \mathbb ℝ^𝑡 \tag{9} \] \(\mathbf R_{ij}^𝑡\) は同期ドット積の要素を再スケールするために使用されます。 \[ \mathbf S_{ij}^𝑡 = \frac{(\mathbf Z_i^𝑡)^⊺· diag(\mathbf R_{ij}^𝑡) ·(\mathbf Z_j^𝑡)}{\sqrt{\sum_{\tau=1}^t \left[\mathbf R_{ij}^t \right]_\tau}} \tag{10} \] 次に、\(\mathbf R_{ij}^𝑡\) が使用されます。直感的に、\(𝑟_{𝑖𝑗}\) の値が大きいほど、ドット積をより最近の内部ティックに偏らせることで、より短期的な依存関係が生じます。一方、\(𝑟_{𝑖𝑗} = 0\) は標準的なドット積を復元します(これもゼロに初期化します)。平方根正規化により、単一の \(𝑖𝑗\) の組み合わせが下流処理を支配するのを防ぎます。(Vaswani et al., 2017)。実際には、サブサンプリングされた同期ペアに対してのみ \(\mathbf R_{ij}^𝑡\) を計算すればよく、これは出力表現とアクション表現に対して個別に行います。 CTMは異なるニューロンペア間で減衰率を変更することを学習できるため、学習可能なパラメータに𝑟を含めることで、CTMのニューラルダイナミクスへの依存度が効果的に高まります。完全な開示のために、CTMはImageNet分類(セクション3を参照)ではこれを一度も活用していないことがわかりました。ImageNet分類では、\(\mathbf S_{out}^𝑡\) 内の8196個の(𝑖,𝑗)ニューロンペアのうち、意味のある減衰を示したのはわずか3個でした。2D迷路のナビゲーション(セクション4を参照)では、\((𝑖,𝑗)\)ペアの約3%に意味のある減衰が見られました。これは、明確な順次推論を伴うタスクでは、より局所的な視点(つまり、同期へのより速い減衰)が必要であることを示しています。同期ドット積の要素を再スケールします。
潜在的なスナップショット依存性の回復 興味深いことに、CTMは現在の状態z𝑡への依存性を回復することを学習できます。\(𝑖 = 𝑗\)と設定し、\(𝑟_{𝑖𝑗}\)が非常に小さい場合、これは\(𝑖\)個のサンプリングされたニューロンごとに\(\mathbf z^𝑡\)の要素ごとの2乗を計算することとほぼ等価です。実際にはこれは不要であることが判明していますが、いくつかのサブサンプリング戦略を検討し、付録B.2でそれらについて説明しました。
CTMは各内部ティック\(𝑡\)で出力を生成します。重要な疑問が生じます。この内部時間次元にわたってモデルをどのように最適化するかです。\(\mathbf y^𝑡 ∈ \mathbb ℝ^𝐶\)を内部ティック𝑡における予測ベクトル(例えば、クラスの確率)とします。ここで𝐶はクラスの数です。𝑦𝑡𝑟𝑢𝑒を真のターゲットとします。各内部ティックにおける損失は、クロスエントロピーなどの標準的な損失関数を用いて計算できます。2
2 実際には、任意の適切な損失関数を使用できます。
\[ \mathcal L^𝑡 = CrossEntropy(\mathbf y^𝑡 , 𝑦_{𝑡𝑟𝑢𝑒}) \tag{11} \] および対応する確実性の尺度 \(\mathbf C^𝑡\) 。確実性は単純に 1 正規化エントロピーとして計算します。 \(𝑡 ∈ \{1, . . . , 𝑇\}\) すべてについて \(\mathcal L^𝑡\) と \(\mathbf C^𝑡\) を計算し、内部ティックあたりの損失と確実性 \(\mathcal L ∈ \mathbb ℝ^𝑇\) と \(\mathbf C ∈ \mathbb ℝ^𝑇\) を生成します。
当然、次のような疑問が生じます。学習のために、\(\mathcal L\) をスカラー損失にどのように縮減すればよいのでしょうか。私たちの損失関数は、内部思考次元全体にわたってCTMのパフォーマンスを最適化するように設計されています。モデルがその特定のステップでのみ出力するように誘導する可能性のある単一のステップ(例えば最後のステップ)に依存するのではなく、2つの内部ティック(損失が最小となるポイントと確実性が最大となるポイント)から情報を動的に集約します。このアプローチにはいくつかの利点があります。(1) CTMが複数の内部ティックにわたって意味のある表現と計算を開発することを促すこと。(2) カリキュラム学習効果が自然に促進され、モデルは最初はより複雑な処理のために後の内部ティックを利用し、徐々により単純な処理のために前のステップに移行することができます。(3) CTMは、データセット内の個々のデータポイントの固有の難易度に基づいて計算を適応させることができます。この目的のために、2つの内部ティックにわたって \(\mathcal L\) を(データポイントごとに)動的に集約します。
最終的な損失は次のように計算されます。 \[ \mathcal L =\frac{\mathcal L^{𝑡_1} + \mathcal L^{𝑡_2}}{2} \tag{12} \] 確率的勾配降下法を用いてモデルパラメータ\(𝜃_{syn}\)と\(𝜃_{𝑑=1...𝐷}\)を最適化します(式1と式3を参照)。
このアプローチにより、CTMは高い確実性が正しい予測に帰属することを確実にしながら、その「最良の」予測を効果的に改善することができます。リスト4は損失の計算方法を示しており、確実性が1 - 正規化エントロピーとして計算されることを示しています。このアプローチにより、CTMは必要に応じて思考プロセスを動的に調整することもできます。
def ctm_loss ( logits , targets ):
B, C, T = logits . shape
# B= minibatch size , C= classes , T= thought steps
# Targets shape : [B]
# Compute certainties as 1 - normalised entropy
p = F. softmax ( logits , 1)
log_p = torch . log_softmax ( logits , 1)
entropy = -torch . sum (p * log_p , dim =1)
max_entropy = torch . log (C)
certainties = 1 - ( entropy / max_entropy )
# Certainties shape : [B, T]
# Expand targets over thought steps
targets_exp = torch . repeat_interleave ( targets . unsqueeze ( -1) , T, -1)
# Loss function could be other things , but we use cross entropy without reduction
loss_fn = nn. CrossEntropyLoss ( reduction ='none ')
# Losses are of shape [B, T]
losses = loss_fn ( predictions , targets_exp )
# Get indices of lowest loss thought steps for each item in the minibatch
lowest_idx = losses . argmin ( -1)
# Get indices of most certain steps for each item in the minibatch
certain_idx = certainties . argmax ( -1)
loss = ( losses [:, lowest_idx ] + losses [:, certain_idx ])/2
return loss . mean ()
リスト 4 | CTM 損失関数。これにより、CTM は特定のデータ ポイントに使用される内部ティックの数に関して柔軟に対応できるようになります。
CTMの基本的な機能要素としてタイミングを導入することには、多くの利点があります。その一つは、CTMが使用する内部ティック数に制限を設けることなく学習できることです。このような自由度は微妙ではありますが、実際には非常に重要で、CTMはデータポイントごとに異なる計算量を割り当てることができます。適応型/動的計算(Graves, 2016)の考え方は、現代のテスト時計算と整合していますが、この求められているモデリング特性は、事後的に適用されたり学習中に制約として課されたりするのではなく、結果としてCTMから除外されるという点が異なります。損失関数には、この動作を明示的に促進するものは何もないことに注意してください。ある意味で、CTMは一種の帰納的バイアスを実装しており、モデリングプロセスの複雑さ(使用される内部ティック数で概算)をデータに合わせて調整できます。これは、難易度が変動する問題(例えば、画像の分類が容易か困難かなど)を解決するための、はるかに自然な手段であると考えています。このような特性が生物学的妥当性の向上の結果として生じることは驚くべきことではありませんが、喜ばしいことです。第5章では、CTMの性能と特性を他のモデルや人間の基準と比較します。
実験的評価
以下のセクションでは、多様な課題における連続思考マシン(CTM)の包括的な評価を示します。これらの実験の主な目的は、CTMの中核となる設計原理、すなわちニューロンレベルの時間処理と、神経同期を直接的な潜在表現として用いること、から生まれる能力と特性を探求することです。内部神経活動の展開を明示的にモデル化し、活用することで、CTMがどのようにして知性のさまざまな側面を必要とする問題にアプローチできるようになるのかを理解することを目指します。
まず、ImageNet-1Kのような標準的な知覚タスクにおけるCTMの解析から始めます(第3節)。CTMの内部ダイナミクスの豊かさ、創発的な推論プロセス、キャリブレーション特性、そして適応的計算に焦点を当てて分析します。その後、CTMとCIFAR-10における人間のパフォーマンスを比較する研究(第5節)と、CIFAR-100におけるアブレーション研究(第6節)を実施します。
次に、内部世界モデルの形成を必要とするように設計された困難な2D迷路ナビゲーションタスクを用いて、CTMの複雑な逐次推論、計画、および空間理解能力を具体的に検証する(第4節)。 さらに実験を行い、思考の時間的展開が重要となる、実数のソート(第7節)や累積パリティ計算(第8節)といったシーケンスベースのタスクにおいて、CTMがアルゴリズム手順を学習し実行する能力を調査する。また、MNIST数字を用いた質問応答タスクを通して、記憶、検索、および記号操作能力をテストする(第9節)。 最後に、CTMを強化学習環境に拡張し、逐次的な意思決定と外部世界との継続的な相互作用への適用可能性を示す(第10節)。
これらの実験は総合的に、計算を神経ダイナミクスに根ざすことでCTMが内部思考プロセスをどのように発達させ、活用できるようになるかについての洞察を提供することを目的としており、従来のモデルとは異なるアプローチを提供し、より生物学的に妥当な人工知能への一歩を踏み出すものです。
このセクションでは、ImageNet-1K分類タスクでCTMをテストします。CTMが分類精度の点で最先端であると主張するわけではありません。最適なトレーニングレシピを見つけるには、かなりの労力とチューニングが必要になります(Vryniotis and Cord, 2021)。むしろ、CTMがこのタスクを解決する方法が斬新であり、検証する価値があると主張しています。モデルのセットアップとハイパーパラメータについては、付録C.1で詳しく説明します。ResNet-152バックボーン3を使用したCTMは、トリミングされていないImageNet-1K検証データ(ただし、画像の短辺の長さが256になるようにスケーリング)で評価した場合、トップ1検証精度72.47%、トップ5検証精度89.89%を達成しました。この結果は現時点では最先端技術と比較できるものではありませんが、ニューラルダイナミクスを表現として用いてImageNet-1Kを分類する初の試みでもあります。今後の進歩、ハイパーパラメータの調整、そしてCTMに合わせた特徴抽出器の開発によって、このギャップを埋められると期待しています。
3 受容野を制限するため、初期畳み込みカーネルを7×7ではなく3×3に変更しました。詳細については付録C.1を参照してください。
図2は、選択した最小確実性に達したときにCTMの内部ティックがどのように切り捨てられるか、および期待されるトップ5精度がどの程度になるかを示しています。例えば、すべてのデータに対して0.5の確実性に達するには、画像あたり20個未満の内部ティックが必要ですが、しきい値を0.8に選択した場合、すべてのデータが常にこのしきい値に達するわけではありません。後者の場合、ユーザーの必要に応じて計算を切り捨てることができます。許容可能な内部しきい値に達したときに内部ティックを停止することで、一種の適応型計算を利用できます。
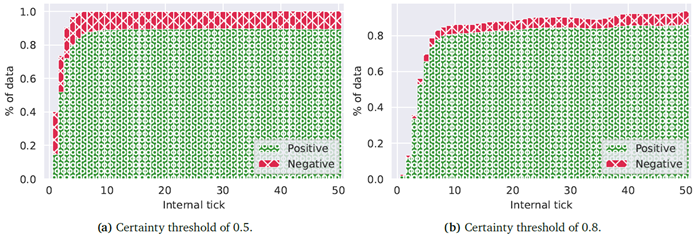
図2 | 固定された確信度の閾値を超えて予測を行った場合のみの上位5つの精度(検証)。低い閾値(a)0.5の場合、CTMは約4内部ティック以降、100%の確率で予測を行いますが、(b)確信度の閾値を0.8に設定すると、データの約80%のみを予測します。これらの評価は、確信度の閾値を調整して適応型計算を可能にし、必要に応じて計算を停止するために使用できます。
予測メカニズム:確実性を考慮する 図3aは、異なる予測メカニズムが全体的なパフォーマンスにどのように影響するかを示しています。ここでは、「瞬間的な」予測(つまり、各内部ティックにおける予測)と、確実性に基づく予測(特定のステップまでの最大確実性、および確実性によってロジットを重み付けした場合)を比較しています。興味深いことに、約15内部ティック以降は、確実性を明示的に考慮することが望ましいことがわかります。ロジットの重み付けされていない平均を使用すると、最悪のパフォーマンスが得られます。これは、CTMが実際に予測を改善するプロセスを経ている一方で、確実性の低い誤った予測を通過する可能性があることを示唆しています。図5bは、さらなる証拠として、確実性の低いインスタンスの具体的な例を示しています。
図3bは、CTMが少なくとも0.8の確信度を生成した場合の内部ティックの分布を示しています。これは、データの大部分が10個未満の内部ティックを必要とし、最大50個の内部ティックに向かって長い裾野を持つことを示しています。図3cのキャリブレーションプロットは、CTMが非常に良好なキャリブレーションを持っていることを示しているため、おそらく最も印象的です。これは、CTMが内部ティックを通じて次第に確信度を増していく様子によるものです。特定のインスタンスの予測確率は、選択されたクラスの内部ティック全体の平均確率であるとみなします。図5のデモンストレーションは、内部ティックを通じて確信度がどのように増加するかを示しています。明らかに、内部プロセスに従うことで、CTMはより信頼性の高いクラス確率を生成できるようです。これは通常、トレーニング後の調整や特別なトレーニング設定を必要とする特性です(Guo et al., 2017)。
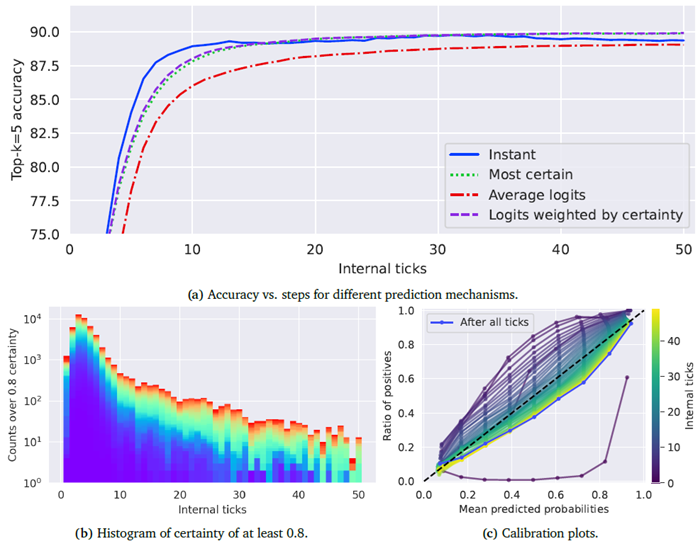
図3 | CTMの性能と有用性の調査。内部ティックとImageNet-1Kの上位5つの精度の関係を示しています。(a)は、4つの異なる方法で出力予測を決定する際の内部ティックに対する精度を示しています。約15ステップまでは、特定の内部ティックでの予測を採用することが合理的であり、そこからは確実性を成功の尺度と見なす方が適切であることを示しています。(b)は、各内部ティックについて、確実性0.8を超えるデータ数のヒストグラムを示しています。色はクラスインデックスを示しています。(c)は、キャリブレーションプロットを示しています。ここでは、CTMの予測確率は、特定の内部ティックまでの平均確率とみなされており、これが良好なモデルキャリブレーションにつながることを示しています。
図4は、このCTMの活性化後の神経ダイナミクスを視覚化したものです。これらのダイナミクスは多様で構造が豊かであり、CTMが行動を起こし、意思決定を行うための表現を形成します。この図の目的は、CTMが実際に多様な神経活動を生み出し、そのダイナミクスを相互の関係(すなわち同期)で測定し、下流のタスクのための強力な潜在表現として使用できることを示すことです。第4節では、このような表現が問題解決において高い有用性を持つことを示す証拠を示します。
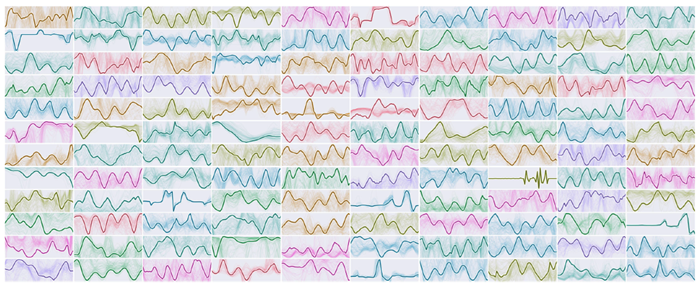
図4|活性化後のニューロンのダイナミクス(図1の5)。各サブプロット(ランダムな色で表示)は、内部の目盛りにおける1つのニューロンのダイナミクスを示しています。異なる画像からの複数の例が薄い背景線で示され、前景の線は1つの例です。データ間の多様性を示すために、複数の例を示しています。同期を計算する際に使用されるのはこれらのダイナミクスであり、CTMの基本的な処理要素を形成します。
まとめ 図4は、CTM内のニューロンが複雑なマルチスケールパターンを示していることを示していますが、これがなぜ有用であるかという実用的な根拠は示していません。これを示した理由は、CTMが真のダイナミクスを構築し、活用している証拠として、つまり、神経活動のパターンが非自明かつ多様であることを示すためです。これらのダイナミクスとそれに含まれる複雑さは、神経計算の背後にある生物学的に妥当なメカニズムに近いと考えられる、新しい種類の表現を形成します。
図5は、CTMがImageNet-1K検証セットをどのように認識しているかを示す例です。付録C.3にさらに例を示します。これらの視覚化は動画で視聴することをお勧めします。動画には50フレーム(内部ティックごとに1フレーム)あり、CTMの内部思考プロセスにおける注意マップの経時的な変化と、異なる領域への移行を示しています。画像のさまざまな部分への注意のスムーズな移行は、トレーニング中に特性として現れます。この一時的な注意の一部を矢印で示し、注意が顕著な領域を直感的に移動する様子を示しました。これらの注意マップの進行の興味深い側面をすべて解明することは、本稿では不可能です。その代わりに、これらの例では、注意パターンが複雑なプロセスを示す様子を示します。また、時間の経過に伴う確実性も示しており、CTMが推論するにつれて確実性が高まる様子を示しています。
CTMは情報検索にアテンションを使用するため、固定サイズの画像に限定されません(また、将来の研究では任意の長さのトークンシーケンスに適用できます)。そのため、我々は切り取られていない検証データで評価を行っています。複数の入力解像度を用いてトークンの階層を構築し、CTMが(学習中ではなく推論中に)多数のトークンの集合に注意を向けるようにすることも考えられますが、この検討は将来の研究のために残しておきます。
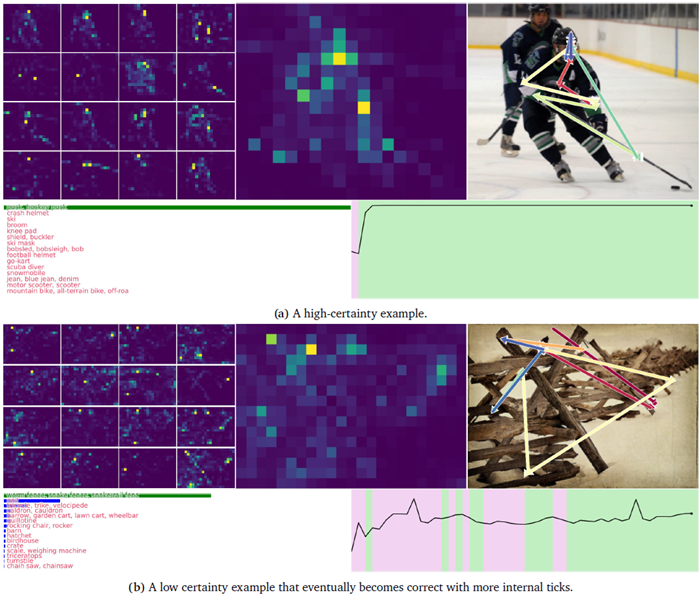
図5 | 検証セットからランダムに抽出されたImageNet-1Kのユースケース。このデモは内部ティックが50個あるため動画として表示するのが最適ですが、ここでは最終ステップのみを示しています。左側には、16個の注意ヘッドすべての重み付けの平均(内部ティック全体)を示し、右側には、全50ステップにおけるそれらの集合平均(詳細は付録C.1を参照)の重心の近似値を赤から青への矢印で示しています。CTMの内部ティックの連続性により、各ヘッドの注意が領域から領域へとスムーズに移行し、時には特定の顕著な特徴(鼻、境界など)に集中したり、時にはより広い領域に広がったり、さらには識別可能な方向(例:下から上へ)に移動したりする様子が見られます。付録C.3には、さらにいくつかのデモが含まれています。
CTMは時間の経過とともに観察を学習します。 実験中、CTMの学習が進むにつれてその機能性を監視しました。本論文では明示的に示していませんが、学習中にニューラルダイナミクスの複雑さ、ひいてはCTMが行う観察プロセスの複雑さが増加します。最初は、CTMは図5のように「周囲を見回す」ことはなく、時間の経過とともにその行動を学習するだけです。Xuら (2015) による初期の研究では、RNNを用いて画像からテキストキャプションを推論する方法が示されました。CTMの推論プロセスは、入力データとターゲットデータの両方から分離された内部次元に沿って展開されるという点で異なりますが、それでも複雑な注意パターンを生み出し、意思決定の際に注意を集中させる場所を強調します。
自然知能に向けての一歩 生物学的知能は、多くの場合、依然としてAIよりも優れています(Chollet et al., 2024; Lake et al., 2017; Phan et al., 2025; Ren and Xia, 2024)。生物学的脳は、従来のニューラルネットワークとは非常に異なる方法でタスクを解決します。これが、その理由を説明できるかもしれません。本研究では、生物学的脳とより一致した方法で問題解決にアプローチするモデルの開発を目指し、この類似性を達成する上での神経ダイナミクスの中心的な役割を強調しました。私たちの観察は、CTMが画像から情報を順次取得するプロセスを実行していることを示唆しています。付録C.3に、興味深い、またはユニークなパターンや結果を示すさらなる例を示します。

図6 | CTMが画像を観察し、思考する様子を観察する様子。付録Jには、UMAP (McInnes et al., 2018) を用いてニューロンがどのように配置されたかの詳細が記載されています。色は、低(青)から高(赤)までの活動レベルを示しています。左上から右下にかけて、内部の目盛りに沿って神経活動の進行を示しています。注意深く観察すると、複数のスケールで明確な構造が見つかります。この視覚化は、動画で見るのが最適です。
最後に比較対象として、低周波進行波について考察する。これは皮質ダイナミクスにおいて広く報告され、様々な神経計算に関与していることが示唆されている現象である(Muller et al., 2018)。図6は、UMAP(McInnes et al., 2018)を用いてCTMのニューロンを2次元特徴空間にマッピングしたものである。この空間における各ニューロンの位置は、その活性化「プロファイル」、すなわち時間と複数の刺激に対する応答パターンによって決定される(付録Jを参照)。このマッピングを内部ティック上で視覚化すると、特徴空間全体に伝播する低周波構造が明らかになる(動画で表示するのが最も効果的である)。重要な点は、CTMがこの構造を明示的な駆動信号なしに創発的に生成することである。同様の現象はKuramoto振動子のネットワークでも発生する(Miyato et al., 2024)。我々のケースでは、波は全対全ネットワークにおいて学習された特徴マップ全体に伝播する。同時進行する研究は、長距離通信のための進行波の明示的な符号化についても研究している(Jacobs et al., 2025)。我々は、これらの観測された波に機能的な意味を与えるのではなく、CTMの思考プロセスにおけるそれらの明確な存在を強調する。
このセクションでは、2次元迷路をツールとして用い、CTMが計画とナビゲーションを行う際の挙動を調査します。2次元迷路の解法は、適切な帰納的バイアス、つまり出力空間が入力空間の次元と一致するようにすることで容易になります。入力空間の各ピクセルにおいて、モデルは2値分類を実行する必要があります。このような設定は、機械が反復的なアルゴリズムによる解を学習できるため(Bansal et al., 2022; Schwarzschild et al., 2021)、設計上機械に適しており、より自然な方法で考える必要がなくなります。それでも、モデルの学習可能性は疑問視されており、多くの場合、大規模な迷路への一般化を優先する慎重なモデル設計や目的関数設計に依存しています(Bansal et al., 2022; Zhang et al., 2025)。このような一般化は、確かに知能の重要な側面の一つです。
しかし、迷路の解を単に見つけることと、思考プロセスに従って解を導き出すことの間には、決定的な違いがあります。このようなシステムの創発的な行動は印象的ですが(例えば、はるかに大きなサイズの迷路への一般化(Bansal et al., 2022))、これらのモデルが知性を示しているかどうかを判断するのは困難です。2D迷路課題をより困難にし、人間のような解法が必要となるようにするにはどうすればよいでしょうか。私たちは以下のことを提案します。
4
これは、一部の迷路では必要な長さよりも短い場合があり、その場合は後のステップを無視します。
5
ルートが100より短いインスタンスには「待機」クラスを使用し、ターゲットベクトルを待機クラスで埋めます。
2D迷路課題のこの新たな表現が、思考プロセスを追跡できるモデルを浮き彫りにする、挑戦的なベンチマークとなることを期待しています。私たちは、迷路データセットリポジトリ(Ivanitskiy et al., 2023)を用いて、訓練用に39×39の迷路、一般化テスト用に99×99の迷路を生成しました 6。比較のために、以下の3つのモデルバリアントを訓練しました。
6 CTM コード リポジトリ を参照してください。
同じ隠し幅を使用した場合、CTMは最も少ないパラメータを必要としました。詳細は付録D.4を参照してください。
図7aは、CTMとベースラインの精度を示しています。FFモデルと最良のLSTMモデルはどちらも過学習の兆候を示しており(損失曲線については付録D.5を参照)、その構造が問題に適していないことを示しています。このタスクで高い精度を達成したのはCTMのみです。私たちの実験では、LSTMで同じ性能を達成することはできませんでしたが、50内部ティックを使用した単層LSTMが最高の性能を達成しました。解を調べると、図7bのオレンジ色の曲線(「LSTM=1、50ティック」)に示すように、LSTMは解を学習し始めていますが、それを超えることはできないことがわかります。
学習可能性 この場合、CTMとLSTMのパフォーマンスに大きな差があることから、学習可能性に関する疑問が生じます。CTMの方がはるかに最適化が容易です。迷路課題の解決は複雑です。なぜなら、データの相互作用を調整し、経路予測を生成し、さらにこれまでの位置の記憶を保持する複雑な表現を作成するモデルが必要だからです(詳細な議論はセクション4.4を参照)。CTMが最小限の変更(予測の形式のみ)でこれを実行できるという事実は、その有用性を証明しています。
図7bは、ホールドアウトテストセットにおける経路長に対する精度を示しています。CTMは明らかに長い迷路を解く能力が高いのに対し、ベースライン手法は早い段階で性能が低下し始め、最も性能の高いLSTMでさえ迷路経路に沿って約20歩進んだところで性能が低下しています。これは、CTMの方が難しい問題を解く学習能力が高いことを示しています。深さ1のLSTMはパラメータ数で最も近い値を示しましたが、すべてのベースラインはより多くのパラメータを持っていました。言い換えれば、CTMの性能が優れているのは、パラメータ数が多いからではなく、ニューラルダイナミクスと同期が有用であるという考え方に基づいているからです。
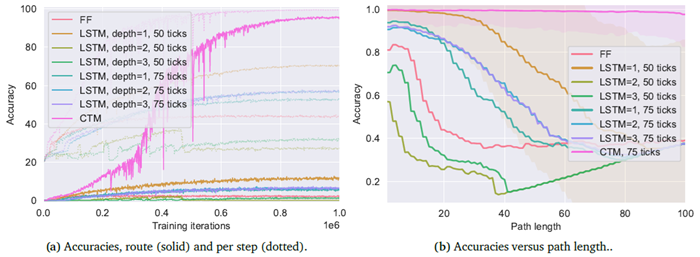
図7 | CTMとフィードフォワードベースラインおよび複数のLSTM設定の比較。CTMは、学習データに十分に適合し(ほぼ完璧な学習精度)、過適合せず(帰納的バイアスの適切な選択を示している(Utgoff, 2012))、長いパスで高いテスト精度を達成する唯一のモデルです。
図8はCTMが辿るプロセスを示しています。時間経過に伴う平均(ヘッド全体)の注意重みを視覚化することで、CTMが迷路の終わりと予測される地点に到達するまで、妥当な経路に沿って系統的に進んでいく様子を見ることができます。この問題解決プロセスは、人間が上から下に向かって迷路を解く方法と全く同じではありません。ここで読者の皆様にご注意いただきたいのは、この迷路解法CTMは位置埋め込みを一切使用していないということです。つまり、迷路を通る経路を辿るためには、迷路の将来の状態を「想像」することで交差注意クエリを作成する必要があるのです。これは人間において「エピソード的未来思考」(Atance and O’Neill, 2001)として知られるプロセスです。

図8 | 自然な迷路解法。各行は、CTMが異なる39×39の迷路を解く様子を示しています。左端の画像は、思考プロセス全体を通して注意の重心を色付きの矢印で示し、CTMが解の経路に沿ってどのように注意を払っているかを示しています。右側の画像は、CTMが異なる内部ティックで出力している解のスナップショットで、注意ヒートマップ(矢印と同じ色)が重ねて表示されています。(a)は典型的な例を示し、(b)は、CTMがトレーニング中に使用した内部ティックを超えて経路に沿って注意を払い続ける様子を示しています(このため、CTMはトレーニング時の2倍の長さで展開します)。プロジェクトページでは、追加の例と、CTMを操作してこのような迷路を解くインタラクティブなデモンストレーションを提供しています。
このCTMは、開始位置から最大100歩先までを予測するように学習されました。図8aでは、CTMが迷路の終点(右端の緑のヒートマップ、約75個の内部目盛り)に注目している様子がわかります。これは、CTMが予測可能な100歩以内であるためです。これに対し、図8bでは、真のパスが100歩をはるかに超えています。学習時に使用したよりも多くの内部目盛りを使用して注意マップを評価すると、注意パターンはパスの残りの部分をトレースし続けます。これらの視覚化を作成するために、学習に使用した内部目盛りの2倍の回数でCTMを実行しました。
この行動は創発的であり、CTMが単に訓練データを記憶するのではなく、基礎となる迷路課題の一般的な手順を学習したことを示唆しています。
次のセクションでは、このCTMが訓練に使用した迷路よりも大きな迷路にどのように一般化できるかを示します。
前のセクションでの観察から、CTMは学習に使用したデータを超えて一般化できる可能性があることが示唆されました。位置埋め込みを一切行わないことにした理由の一つは、このようなモデルは変更を加えることなくあらゆるサイズの迷路に適用できるからです。これを検証するために、CTMをより長い経路とより大きな迷路に適用しました。設定は以下のようにしました。
図9は、より長い経路やより大きな迷路に一般化した場合の結果を示しています。CTMは39×39の迷路ではどの長さの経路でもほぼ完璧なパフォーマンスを発揮しますが、99×99のより大きな迷路ではパフォーマンスが低下し始めます。これはおそらく、大きな迷路では開始点と終了点間の絶対距離が大きくなるためです。今後の研究では、以下の連続的なトレーニング方法を検討する予定です。(1) CTMによって予測された終了点を考慮し、(2) 現在のニューラルダイナミクスを維持し、(3) 開始点を予測された終了点に「テレポート」し、(4) そこから次のミニバッチを継続します。このような設定は、CTMのシーケンシャルな性質により適しています。読者の皆様には、プロジェクトページにあるインタラクティブなデモをご利用いただき、CTMを操作してこのような迷路を解くことができることをお勧めします。「オープンワールド」トレーニングに関する議論については、セクション12の今後の研究に関する議論を参照してください。
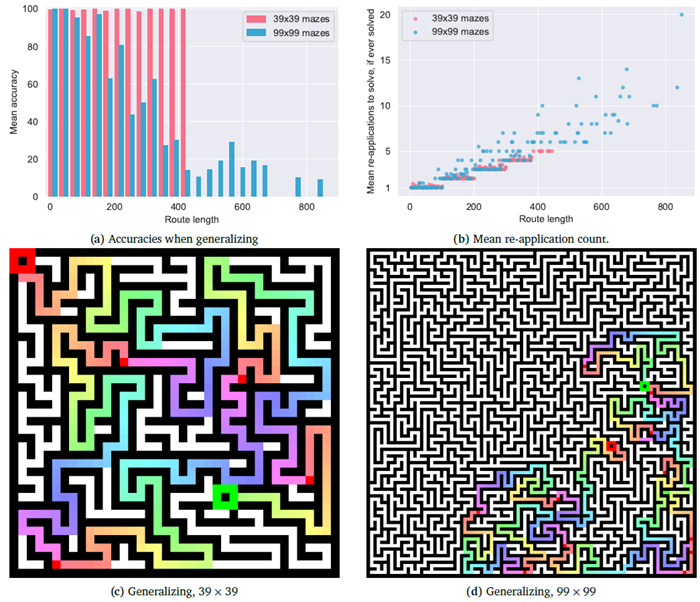
図9 | より長い経路とより大きな迷路に一般化した場合のCTMの精度。このCTMは、経路長100(トレーニングデータでは経路長が長い場合は切り捨て)までの39×39サイズの迷路を解くように学習されました。(b)では、開始点をCTMが特定の迷路に対して予測する終点に移動すると「再適用」が発生します。(c) 39×39と(d) 99×99の迷路の一般化例を示します。虹色(赤から青)は、再適用ごとの予測ステップ数を示しています。初期の開始点と終点は、見やすさを考慮して大きく表示されています。
世界の内部モデルと認知マップは、知能システムの重要な側面を表しています(Gornet and Thomson, 2024; Ha and Schmidhuber, 2018; LeCun, 2022)。この場合、世界モデルとは外部環境の内部表現であり、エージェントの世界の構造、ダイナミクス、そしてその中での自身の行動可能な位置に関する知識を包含するものであると考えます。優れた世界モデルは、エージェントが世界について推論し、計画を立て、行動の結果を予測できるようにする必要があります。認知マップ(Gornet and Thomson, 2024)は、特に空間関係とナビゲーションに焦点を当てています。これらの内部表現を構築し、活用する能力は、高度な知能の強力な指標であり、おそらく前提条件でもあります。「エピソード的未来思考」という概念(Atance and O’Neill, 2001)は、人間の知能の代表的な特徴とさえ考えられています。世界モデルを持たないエージェントは、反応的な行動しかとれません。同様に、認知マップを持たないエージェントは、複雑な空間環境内を効果的に移動したり相互作用したりする能力が著しく制限されます。したがって、世界モデルと認知マップの存在と洗練度は、知能を評価するためのベンチマークとして役立ちます。
この目的のため、我々は迷路課題を、解くために優れた内部世界モデルが必要となるように設計した。これは、(1) 局所アルゴリズムで迷路を解くのではなく、モデルが直接経路を出力することを要求すること (Schwarzschild et al., 2021)、(2) 画像表現における位置の埋め込みを放棄すること、つまり、モデルが課題を解決するために独自の空間認知マップを構築する必要があること (Gornet and Thomson, 2024) によって実現された。実際、CTMのNLMと同期コンポーネントにより、CTMは2D迷路課題を解くことができ、訓練した最高のベースラインをはるかに上回る結果が得られた。これらの結果は、CTMが環境の内部モデルを構築し、活用する能力がより優れていることを示唆している。
このセクションでは、CIFAR-10を用いてCTMをテストし、人間のパフォーマンス、フィードフォワード(FF)ベースライン、およびLSTMベースラインと比較します。モデルベースのベースラインでは、特徴量化後のモデル構造(CTM、LSTM、FF)による差異を強調するために、制約付き特徴量化バックボーンを使用しました。また、CTMとLSTMに「考える時間」を与えるために、50の内部ティックを使用しました。アーキテクチャの詳細は付録Eに記載しています。人間のベースラインとモデルのベースラインは、次のように設定されました。
7 CIFAR-10D は https://sites.google.com/site/hophuoctien/projects/virec/cifar10-c lassification でご覧いただけます。CIFAR-10H は https://github.com/jcpeterson/cifar-10h でご覧いただけます。
図10は、CTM、FF、LSTMモデルの学習曲線と、それぞれのキャリブレーションプロットを示しています。これには、CIFAR-10Hを用いた人間によるキャリブレーションの推定値も含まれています。FFベースラインは早い段階で高い学習精度に達しますが、汎化ギャップが小さいことも示されています。LSTMは学習中の安定性が低く(このため、すべての実験で学習率を0.0001に設定する必要がありました)、テスト精度がわずかに向上しています。CTMはより安定しており、パフォーマンスも優れています。
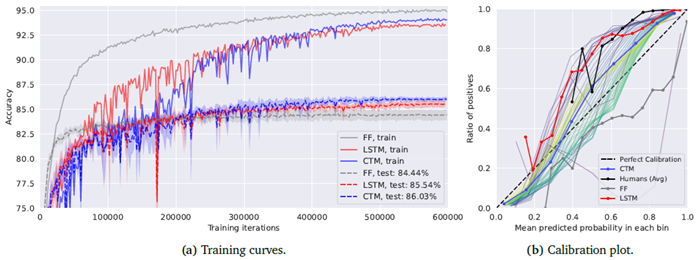
図10 | CIFAR-10の学習曲線(3シードの平均)と、CTM、フィードフォワードのみのベースライン、LSTMベースラインのキャリブレーションプロット。CTMはLSTMよりもフォワードパスあたり±2.4倍遅いものの、学習中はより安定しています。CTMは最高のテスト性能を示しています。キャリブレーションプロットを見ると、人間のベースライン(Peterson et al., 2019)でさえキャリブレーションが不十分であるのに対し、CTMは良好なキャリブレーションを示しており、人間と驚くほど似た方法で失敗していることがわかります。
人間によるキャリブレーションには、CIFAR-10Hで提供されている確率を使用しました。これは、複数の人間による推測に基づいて計算されたものです。ここでも、ImageNet-1Kと同様にキャリブレーションを計算しました(図3c参照)。つまり、選択されたクラスのすべての内部ティックにおける平均確率として予測確率を計算しました。どのモデルも完璧にキャリブレーションされているわけではありませんが、CTMは人間と比較しても最高のキャリブレーションを示しています。驚くべきことに、CTMは人間よりも優れたキャリブレーションを示していますが、LSTMは人間の自信不足を反映しています。
図11aは、CIFAR-10Dデータセットを用いて決定された難易度に対して、モデルとCIFAR-10Hを比較しています。この場合、各モデルと人間は同様の傾向を示していますが、CTMはCIFAR-10Hに最もよく似ています。図11bと11cは、CTMとLSTMの不確実性を人間の不確実性と比較しています(不確実性の代理としてCIFAR-10Hの反応時間を使用)。CTMとLSTMの不確実性は、正規化エントロピー(セクション2.5を参照)を内部ティックで平均して計算します。これは、各モデルが観測データに関して持つ全体的な不確実性を近似するためです。CTMとLSTMはどちらも人間の反応時間と同様の傾向を示しています。
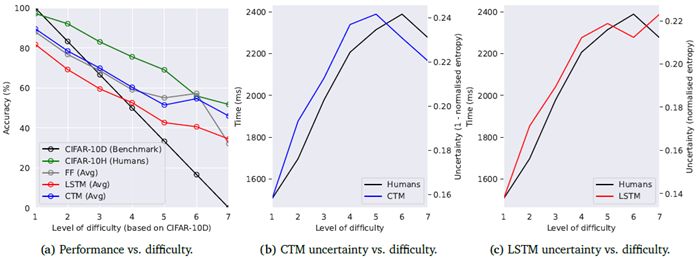
図11|モデルと人間のパフォーマンスと難易度の関係分析。Ho-Phuoc (2018) の難易度較正を使用し、CIFAR-10H (Peterson et al., 2019) の人間の予測値と比較しました。人間の反応時間は不確実性の適切な代理指標であると仮定し、これをCTMとパラメータマッチングされたLSTMベースラインの不確実性の傾向と比較します。ここで視覚化されている誤差は、尺度標準偏差です。
図12は、CTMとLSTMベースラインの神経活動を示しています。CTMは、周期的な動作(周期的な駆動関数は存在しない)を含む複数の興味深い特徴を備えた、豊かで多様かつ複雑なダイナミクスを生み出します。CTMとLSTMの神経活動の明確な違いは、CTMの2つの新しい要素(NLMと表現としての同期)が、神経ダイナミクスを基本的な計算ツールとして利用できることの証拠です。

図12 | CTMとLSTMベースラインのニューロントレース。CTMがCIFAR-10の分類時においても複雑なニューラルダイナミクスを生成・利用している様子を示しています。LSTMはここに示した活性化後の履歴においてある程度の動的な挙動を示していますが、LSTMほどの程度ではありません。各サブプロット(ランダムな色で表示)は、内部の目盛りにおける1つのニューロンの活動を示しています。異なる画像の複数の例は薄い背景線で示され、前景の線はランダムに選択された例から取得されています。
このセクションでは、CTMの2つの側面、(1)幅(つまりニューロン数)、(2)内部ティック数について考察します。CIFAR-100はCIFAR-10よりも難易度が高いデータセットでありながら、計算負荷は比較的低いため、以下の実験ではCIFAR-100を使用しました。
図13aは、固定バックボーンネットワーク(詳細は付録F.1を参照)におけるCIFAR-100の精度とモデル幅(ニューロン数)の関係を示しています。この図では、テスト性能がある程度向上した後、性能が低下していることがわかります。この性能低下は過学習に関連している可能性もありますが、モデル幅が広くなるほどより多くのトレーニングが必要になる(トレーニング反復回数は固定)ことも原因の一つと考えられます。
図13bと13cは、モデルの幅とニューロン活動の多様性の関係を示しています。 直感的に、ニューロン数が多いほどニューロン活動の度合いも高くなると予想されますが、これらの分布はまさにそのことを示しています。図13bでは、ニューロンレベルでデータポイント全体(全ニューロン平均)のコサイン類似度を測定すると、モデルの幅が広いほどゼロ付近の分布が狭くなっていることがわかります。これは、モデルの幅が広いほどニューロンの類似度が低くなることを意味します。これは、CTMがニューロンの数が多いほど、ニューラルダイナミクスにおいてデータポイントに関するより多くの情報をエンコードできることを示しています。図13cは、同様の量を示しています。これは、同じデータポイントについてニューロン間のコサイン類似度を測定したもの(多くの異なるデータポイント平均)です。この場合、モデルの幅が広いほど分布がわずかに狭くなるだけです。
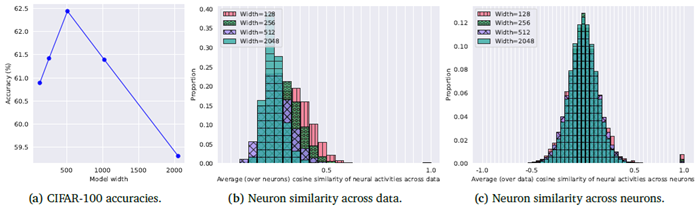
図13 | 異なるモデル幅におけるCIFAR-100の精度とニューロン類似度。(b) データ全体のニューロン類似度については、128枚の画像サンプルにおけるすべてのニューロンペアについて、対応するニューロン間の平均(ニューロン全体)コサイン類似度を計算しました。各バーは、この平均ニューロン類似度を持つ画像ペアの割合です。(c) ニューロン全体のニューロン類似度については、各モデル内のすべてのニューロンペアについて、平均(データ全体)コサイン類似度を計算しました。各バーは、この平均コサイン類似度を持つニューロンの割合です。コサイン類似度が0に絶対的に近いほど、非類似性が高く、ニューロンの多様性が向上していることを示します。
図14は、内部ティックがCTMに与える影響を示しており、(a) 内部ティックに対する精度と、(b) CTMが最も確実性の高い内部ティックの分布を示しています。図14aの精度はほぼ同じですが、50個の内部ティックを使用したCTMが最も高いパフォーマンスを示しました。これは、内部ティックの数が多いほど、より多くのトレーニングが必要であることを改めて示唆しています。
図14bにおいて、確信度の高い領域が2つ出現していることは興味深い。これは、これらのCTMが、データに応じて内部的に2つの異なるプロセスを経て、より多くの「考える時間」を持つことで実際に恩恵を受けていることを示しているからである。なぜこのような結果が現れるかを正確に説明するのは困難であるが、これらの分布が均一とは程遠いという事実は、単に結果を厳密にフィードフォワード的に計算するよりも複雑なプロセスがあることを示唆しており、今後の研究ではさらなる分析が必要である。
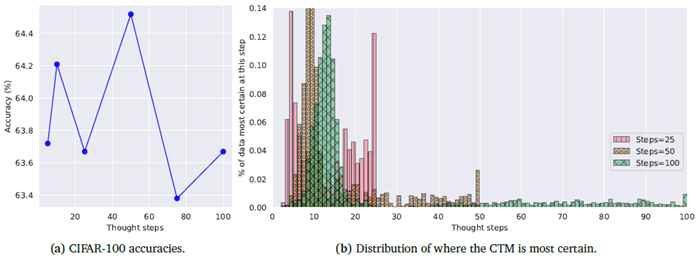
図14 | CIFAR-100の精度と内部ティック分析。(b)の分布と精度は、CTMが最も確実であった内部ティック(x軸)について計算されたものである(セクション2.5参照)。いずれの場合も、CTMには、使用される内部ティックの数に関わらず、初期と後期の2つの確実性領域が存在する。
このセクションでは、正規分布から抽出された30個の数値をソートするタスクにCTMを適用します。 実数のソートは、Graves (2016) が適応型計算用のRNNを設計する際に検討したタスクであり、CTMのような適応型計算システムにおける計算の役割を理解するためのテストベッドを提供します。この場合、CTMはアテンションを使用せず、ランダムにシャッフルされた入力データ(30個の実数)を直接取り込みます。これは、図1の⑩をアテンション機構に置き換え、単純な連結に置き換えることで実装されます。
CTMは時系列出力を生成できるか? この実験では、CTMを内部ティック全体にわたってシーケンスを出力するように設定しました。これはシーケンスをモデリングするためのより標準的なアプローチであり、CTMをこの方法でトレーニングできるかどうかを理解したかったのです。各内部ティックにおいて、CTMは長さ31のベクトルを出力します。これには、ソート用の30個のインデックスと、よく知られているコネクショニスト時間分類(CTC)損失(Graves et al., 2006)に使用される「空白」トークンが含まれます。次に、このCTC損失をCTMの内部ティック全体にわたる出力に適用しました。
図15は、ソートタスクにおけるCTMの結果を示しています。CTMが辿るプロセスには明確なパターンがあり、待機時間と現在のシーケンスインデックス(a)、および出力中の前の値と現在の値の差(b)との相関関係が見られます。同様のタスクがGraves (2016)によって検討されており、適応型計算RNNを用いて15個の数値をソートしました。彼らのケースでは、出力開始前(最初のシーケンス要素に類似)とシーケンスの終了近くで同様の待機時間が観測されました。待機時間と現在のデータ値と前のデータ値の差(図15bで「データデルタ」と呼んでいるもの)の関係を分析した結果、CTMがデータのレイアウトに依存する内部アルゴリズムを使用していることが示されました。また、このCTMがトレーニングデータ以外の分布にも一般化できることも示しています。
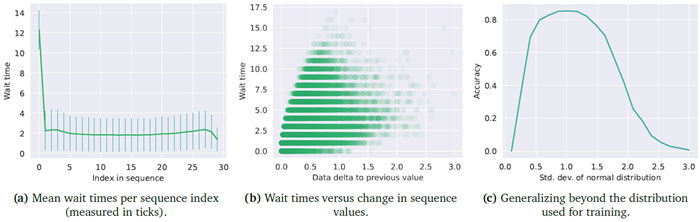
図15 | N(0,𝐼30)でソートした結果。(a)では、平均待ち時間に明らかなパターンが見られます。初期の待ち時間(内部ティック数)は長く、その後最低値まで下がり、シーケンスの終わりに向かってわずかに上昇しています。(b)では、CTMがさまざまな待ち時間を採用していますが、前回の出力値と現在の出力値の差(「データデルタ」)が待ち時間に影響を与えていることがわかります。(c)では、このCTMが異なる正規分布から抽出されたデータにどのように適応できるかがわかります。
図16は、実際のユースケースにおけるCTMの待機時間を示しています。赤いバーは、特定のインデックスの平均よりも長い待機時間を示し、緑のバーは平均よりも短い待機時間を示しています。待機時間が長くなると、データポイント間のギャップ(図15bの「データデルタ」)が大きくなる傾向があります。
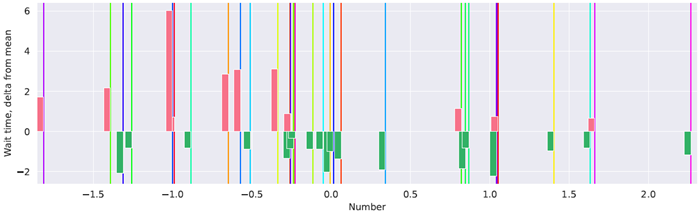
図16 | ソートのデモンストレーション。入力データは縦線で表され、その色は元のシャッフル位置(「レインボー」カラーマップでは紫から赤)を表します。赤と緑のバーは、それぞれ平均待ち時間(シーケンス内の各インデックスについて図15aを参照)からの正と負の偏差を示します。
バイナリシーケンスのパリティは、その要素の積の符号によって与えられます。シーケンスを要素ごとに処理する際、RNN は内部状態を維持し、負の数に遭遇するたびに内部の「スイッチ」を切り替えることでパリティを計算できると考えられます。しかし、シーケンス全体が同時に提供されると、入力に含まれる異なるパターンの数が増えるため、タスクの難易度が上昇します。以前の研究 (Graves, 2016) では、静的に提示されたデータに対してシーケンシャルアルゴリズムを学習できるリカレントモデルを用いてこの課題に取り組んでいます。このように提示されたパリティ計算は、CTM の能力をテストするのに適しています。
ランダムな位置に値1と-1を含む64ビット長のシーケンスのパリティを計算するタスクにCTMを適用します。Graves (2016)とは異なり、モデルがシーケンスの最終パリティだけでなく、すべてのインデックスにおける累積パリティを計算するようにタスクを設定します。例を図17に示します。値-1と1は、入力データの取り込みにAttentionを使用し、位置埋め込みと組み合わせた学習可能なベクトルとして埋め込まれます。CTMは、セクション2.5で説明した損失関数を用いて学習します。ベースラインとしてLSTMも学習しましたが、LSTM学習において最良の結果と安定性が得られるため、最終反復を𝑡2に設定しました。詳細は付録Gを参照してください。
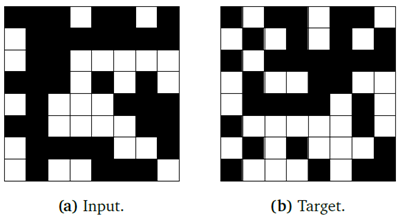
図17 | パリティタスク。入力(a)は64個のバイナリ値のシーケンス(左上から右下)であり、ターゲット(b)は各位置における累積パリティです。ここで、□は正パリティ、■は負パリティを示します。
精度は思考時間とともに向上します。 図18aと18bは、CTMの様々な構成における学習曲線と最終的な精度を示しています。ここでは、内部ティック数(𝑇)とメモリ長(𝑀)を変化させています。また、比較のために、パラメータを一致させたLSTMベースラインもプロットしています。 一般的に、CTMの精度は内部ティック数が増えるにつれて向上します。最も優れたモデルは、内部ティック数が75または100のCTMで、シード実行によっては100%の精度に達することもありました。一方、LSTMベースラインはタスクの学習に苦労し、内部ティック数が10の最も優れたLSTMでも、精度は67% ± 0.05%でした。内部ティック数が10を超えるLSTMベースラインは、学習が不安定な挙動を示しています。これは、第4.1節で述べた、単純な回帰モデルは必ずしも内部思考プロセスの展開に適しているわけではないという観察結果と一致しています。CTMははるかに安定した学習結果を示していますが、ランダムシードの選択により最終的な精度にかなりのばらつきがあります。この点については付録G.4で詳しく説明します。
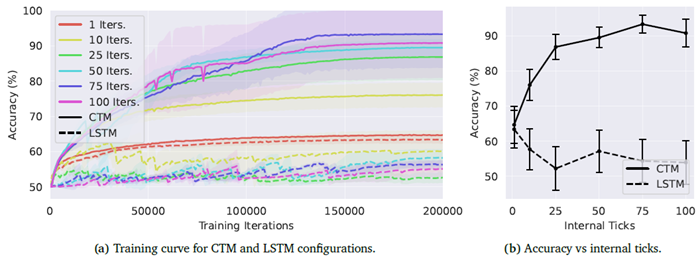
図18 | 様々なCTMおよびLSTM構成における学習曲線(左)と、内部ティックに対する最終精度(右)。 網掛け部分とエラーバーは、シード間の1標準偏差を表します。CTMでは、思考時間の増加がパフォーマンスの向上につながります。
CTMはシーケンシャルアルゴリズムを学習します。 CTMがパリティタスクをどのように解決するかを分析するために、図19は、入力シーケンス内の64個の要素それぞれについて、トレーニングのさまざまな段階で、3つの異なる内部ティック構成における精度を示しています。モデルはまず、最初の要素のパリティを予測することを学習し、トレーニングが進むにつれて、より後の要素の位置を予測することを学習します。内部ティックが増えるほど、モデルはターゲットシーケンス内のより多くの要素を正確に予測できます。

図19 | 様々な内部ティック構成における、異なるトレーニング段階(色で表示)での64要素シーケンス全体の精度。トレーニング初期段階では、すべてのCTMはシーケンスの最初の要素についてのみパリティを正確に予測し、トレーニングが進むにつれて後の要素のパリティ予測精度は徐々に向上します。内部ティックの数が多いモデルはより高い精度を達成し、10ステップモデル(a)はシーケンスの約半分を正しく予測し、75ステップモデル(c)は累積パリティシーケンス全体を正しく予測します。
モデルが累積パリティタスクをどのように解くかを理解するために、2つの異なるモデルについて、トレーニングの複数の段階における全64要素におけるCTMの注意パターン、精度、および最も確信度の高いポイントを図20に視覚化しました。注意と確信度のパターンは、これらのCTMが累積パリティタスクを解くために異なるアルゴリズムを活用していることを示しています。100内部ティックを使用する場合、注意はシーケンスの先頭から末尾に移動し、それに伴い、モデルはその位置での予測の確信度を高めます。一方、75反復のCTMは、シーケンスを逆順に注意するように学習し、最後の内部ティック中にシーケンスの大部分のパリティを同時に正確に予測します。このデータの逆方向検索は、CTMが何らかの計画を実行し、シーケンスの累積パリティに関する最終決定を下す前に、観測データに対する理解を深めていることを示唆しています。これらの結果は、この課題を解決するための複数の戦略が存在し、その中には他の戦略よりも解釈しやすいものもあるものの、CTMは戦略を形成し、それに従う能力を明確に示していることを強調しています。
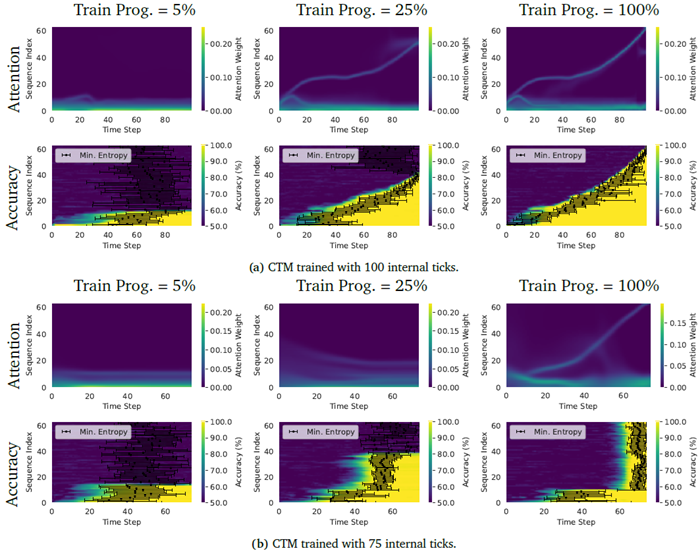
図20 | 100内部ティック(a)と75内部ティック(b)で学習したCTMの、学習中の異なる時点における注意パターン(上)と精度(下)。精度プロットの黒い点は、モデルが最大の確信度に達した内部ティックを示し、エラーバーはサンプル全体の1標準偏差を示す。
図21に2つのデモンストレーションを示します。最初の例(上)は、データセットの典型的なサンプルを示しており、ランダムな位置に1と-1の値が含まれています。この場合、CTMは累積パリティを完全に予測します。アテンションヘッドのダイナミクス(a)は、図20と一致して、アテンションが入力データ内を順次移動していることを示しています。さらに、一部のヘッドは正または負の値のみに注意を払い、他のヘッドは両方の値に注意を払っていることがわかります。2番目の例(下)は、モデルの失敗例を示しています。正のパリティのみを含む入力シーケンスが提示された場合、モデルは累積パリティを正確に予測するのに苦労し、エッジケースの制限が浮き彫りになります。

図21 | パリティ課題の2つのサンプルソリューションにおけるアテンションダイナミクスの可視化。上段 (a, b, c) は完璧な予測を、下段は失敗したケース (d, e, f) を示しています。8つのアテンションヘッドそれぞれに対するアテンション軌跡(アテンション重みにおけるargmaxの位置)は (a, d) に示されています。各点は、特定のタイムステップにおけるアテンション重みが最も高い入力位置を示しています。色は時間経過による変化を表し、明るい色はより遅い内部ティックを示しています。十字 (×) は、モデルが予測において最大の確信度に達したタイムステップを示しています。アテンションヘッドは通常、入力位置を順番に移動します。あるヘッドは一貫して正または負の入力値のみに注意を向けますが、他のヘッドは正と負の入力値を交互に注意を向けます。同様に、あるヘッドは比較的静止したままですが、他のヘッドはデータ上を素早く移動します。(b, e) モデルの予測。(c, f) ターゲット。
CTMの記憶、検索、算術計算能力を評価するために、Manhaeveら (2018) やSchlagとSchmidhuber (2021) を彷彿とさせる質問応答(Q&A)MNISTタスクを考案しました。このタスクでは、モデルは一連のMNIST数字(LeCunら、1998)を順次観測し、続いて、観測された数字の中からどの数字を選択し、それらに対してどのモジュラー演算を実行するかを決定する、織り交ぜられた一連のインデックスと演算子の埋め込みを適用します。これにより、CTMが、画像に描かれた数字や数字間の関係に関する事前知識なしに、手描きの数字を認識し、以前の観測を思い出し、それらに対して論理計算を実行できるかどうかを調べることができます。さらに、訓練時に観測されたよりも多くの演算を推論時に適用することで、CTMの一般化可能性をテストできます。
具体的には、モデルはまず、𝑁𝑑 MNIST の数字を𝑡𝑑 内部ティックごとに順次観測します。次に、モデルは𝑁idx インデックス埋め込み(選択する数字を示す)と𝑁op 演算子埋め込み(モジュラー加算または減算のいずれかを指定し、各中間結果は 0~9 の範囲に収まるように 10 を法として取られる)の織り交ぜたシーケンスを受け取ります。これらはそれぞれ𝑡idx と𝑡op 内部ティックごとに提示されます。最後に、モデルは𝑡ans 内部ティックのゼロテンソルを観測し、モデルに答えを生成するように指示します。0~9 の間のターゲットは、指定されたすべてのモジュラー算術演算の合成から得られます。例を図 22 に示します。
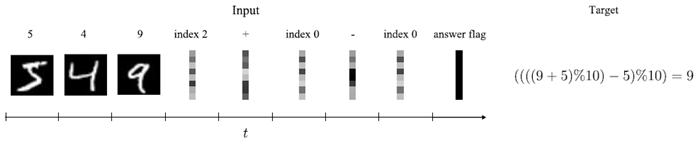
図22 | Q&A MNISTタスクの概要。モデルは、一連の数字とそれに続く一連のインデックスと演算子の埋め込みを観測します。各埋め込みは、複数の内部ティックで繰り返されます。その後、モデルは回答フラグを表示され、モジュラー演算の結果を予測する必要があります。
我々は、各入力を処理するために使用される内部ティックの数を変化させた2つの異なる構成でCTMとパラメータマッチングLSTMを学習させた。数字と埋め込みは1または10内部ティックで観測され、対応する応答時間も1または10内部ティックであった。数字の数と操作数は1から4の間で均一にサンプリングされた。入力あたり1および10内部ティックのCTMのメモリ長は、それぞれ3ステップと30ステップに設定された。これらの観測およびメモリ長の構成では、応答段階で数字の観測が常にメモリ長サイズのウィンドウの外側にあることを強調しておく。このように、CTMは後の時間ステップで数字を思い出すことができるように活性化を整理する必要がある。CTMは、セクション2.5で定義された損失で学習され、最後の𝑡ansステップでのみ計算される。もう一度、LSTMの安定学習のために、𝑡2を最後の反復回数として設定します。詳細な概要は付録Hに記載されています。
同期によるメモリ。 CTMとパラメータマッチングされたLSTMの3回のシード実行のトレーニング曲線を図23に示します。内部ティックが1つの場合、LSTMは当初CTMよりも優れたパフォーマンスを発揮します。内部ティックの数が増えるにつれて、LSTMのパフォーマンスは低下し、学習は著しく不安定になります。対照的に、CTMは思考時間を増やすことで着実にパフォーマンスを向上させます。具体的には、入力ごとに10個の内部ティックを持つCTMの3回のシード実行はすべて、最も困難な分布内タスク(4桁の数字を観測した後に4つの演算を実行する)で96%以上の精度を達成しました。対照的に、対応する10個の内部ティックのLSTMは、すべてのシード実行で21%以下の精度を達成しました。単一ティックLSTMの優れたパフォーマンスは、LSTMの複雑なゲート更新の有効性を浮き彫りにしています。しかし、このメカニズムは、内部ティックを効果的に利用して同期表現を構築するCTMとは異なり、複数の内部ステップに効果的に拡張できません。
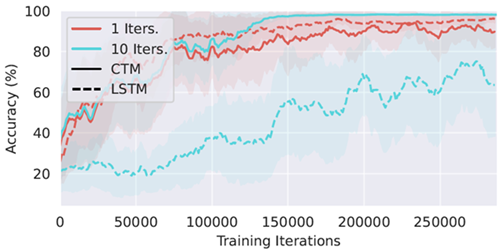
図23 | Q&A MNISTタスクにおけるCTMとLSTMの学習曲線。網掛け部分はシード間の1標準偏差を表す。内部ティックが1つの場合、LSTMはCTMよりも優れた性能を示す。しかし、CTMの性能は内部ティックの数が増えるにつれて向上するのに対し、LSTMはますます不安定になる。
CTMは、観測された数字が記憶ウィンドウの外にある場合でも良好なパフォーマンスを示しました。これは、ニューロンの組織化と同期のみによって、観測した内容をある程度記憶することを学習したことを示しています。CTMの優れたパフォーマンスは、ニューロンの活動の同期を通じてタイミング情報を処理することが、記憶と想起のための強力なメカニズムである可能性を示唆しています。
CTMは一般化できます。 訓練中に使用されたよりも多くの桁数またはインデックス演算子の埋め込みが与えられた場合のモデルの精度を測定することで、一般化を調べます。図24は、表示される桁数と実行する演算の関数としてのCTMとLSTMの精度を示しており、訓練レジームは赤で強調表示されています。CTMとLSTMのベースラインはどちらも、演算数の増加に対して一般化できることがわかります。モデルが分布外に一般化できる仕組みを理解するために、図25にCTMの思考プロセスの例を示します。図25は、入力のサンプルシーケンスと出力ロジットのスナップショットを示しています。CTMは、最終解フラグを待って最終解を一度に決定するのではなく、埋め込みが観測されるにつれてモジュラー計算を順次実行していることがわかります。同様の動作は、1内部ティックのLSTMベースラインでも見られます。 CTMがLSTMにはできないことができると主張しているのではなく、CTMがこのタスクを解決するためのツールとして同期を使用することを学習でき、その結果が効果的であり、より長いタスク要件にも拡張可能であると主張しているのです。
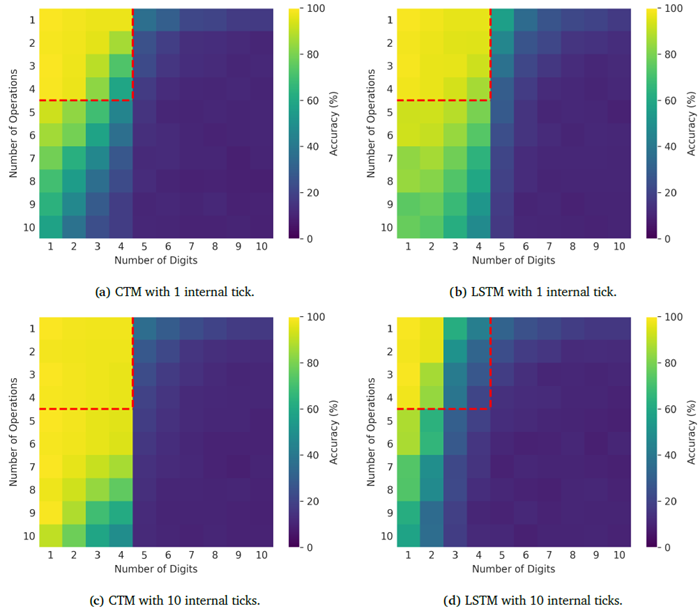
図24 | 内部ティックが1および10のCTMモデルとLSTMモデルのQ&A MNISTタスクにおける一般化可能性。X軸はモデルに入力されたMNIST桁数、Y軸はモデルが実行する必要がある演算回数を示し、色はテスト精度に対応しています。
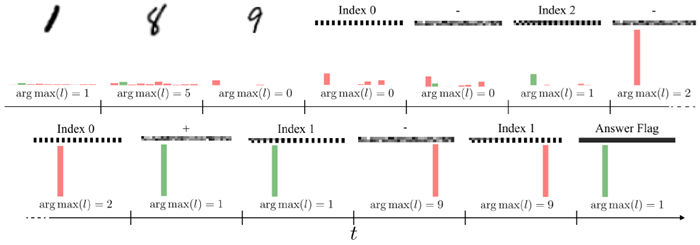
図25 | Q&A MNISTタスクにおけるCTMの思考プロセスの例。モデルへの入力(MNISTの数字、インデックス、演算子の埋め込み)と、異なるスナップショットにおける出力ロジット𝑙のargmaxが示されている。各入力は10内部ティック繰り返される。この場合、モデルは((((((1 − 9)%10) − 1)%10 + 8)%10 − 8)%10)を計算する。モデルは埋め込みが観測されるにつれてこの構成の各部分を順番に計算し、出力は2、1、9、そして最後に同期表現から投影された正解1となることがわかる。
我々は以前、CTMが分離した内部再帰を用いて、非シーケンシャルなタスクをシーケンシャルに処理できることを示した。本稿では、CTMを外部環境との相互作用を伴うシーケンシャルな意思決定タスクに拡張する。具体的には、強化学習(RL)を用いてCTMを訓練する。RLでは、モデルは環境の観察と試行錯誤に基づく行動選択ポリシーを学習する。この設定では、CTMは環境を次の状態に遷移させる行動を生成する前に、1つ以上の内部ティックを処理する。これを実現するために、我々はこれらの内部ティック全体にわたるニューロンダイナミクスを、連続する環境ステップにわたって継続的に維持し、以前の環境観察がNLMを介して現在の内部状態に影響を与えることを可能にする。本節の中心的な目標は、CTMが連続環境で学習するように設定可能であるという証拠を示すことである。
環境:我々は、Gymnasium (Barto et al., 1983; Chevalier-Boisvert et al., 2023; Sutton, 1995; Towers et al., 2024) に実装された2つの古典的な制御タスクと1つのナビゲーションタスク、すなわちCart-Pole、Acrobot、およびMiniGrid Four RoomsでCTMをテストします。これらのタスクの例を図26に示します。CTMは環境遷移にわたって活性化履歴を維持するため、状態のある再帰型ニューラルネットワークとして機能します。したがって、我々は特に、RNNが効果的な部分観測設定でCTMを評価します (Hausknecht and Stone, 2015)。部分観測性は、制御タスクでは位置と角速度の観測成分をマスクし、ナビゲーションタスクでは視野を制限することで導入されます。このマスキングにより、これらのタスクは部分観測マルコフ決定過程(POMDP)に変換され、CTMは過去の観測を想起する方策を開発する必要があります。例えば、Acrobotタスクでは、正しい行動を選択するには、過去の位置を想起し、腕の挙上速度を推測する必要があります。
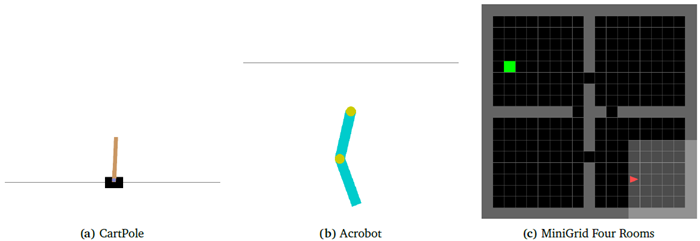
図26 | 強化学習環境。CartPole (a) では、エージェントは2つの離散アクション(左または右)を使用してカート上のポールのバランスを取ります。観測値には、カートの位置とポールの角度という2つの非マスク入力が含まれます。Acrobot (b) では、エージェントは4つの非マスク入力(関節角度の正弦と余弦)を使用して、2関節アームに3つのトルク(+1、-1、または0)のいずれかを適用し、アームの先端を目標高さより上に上げます。MiniGrid Four Rooms (c) では、エージェントは7つの離散アクション(左折、右折など)を使用して移動し、7×7の限られた視野内で、オブジェクト、色、状態IDをエンコードした3×7×7の入力テンソルを観測します。
アーキテクチャ RLタスクでは、以下のアーキテクチャが使用され、Proximal Policy Optimization (Schulman et al., 2017) を用いて学習されます。まず、入力観測値は一連の全結合層を用いて処理されます。ナビゲーションタスクでは、観測状態の埋め込みと、エージェントの視野内の位置に対応する位置埋め込みの追加も含まれます。この表現は、アテンションメカニズムを使用せずに、CTMによって一定時間内部ティック処理され、その後、同期ベクトルが出力され、アクターヘッドとクリティックヘッドによって処理されます。このアプローチを、パラメータマッチングLSTMベースラインと比較します。パラメータマッチングLSTMベースラインでは、内部ティックはLSTMセルによって処理され、LSTMセルは隠れ状態をアクターネットワークとクリティックネットワークに出力します。この比較の目的は、あるアーキテクチャの優位性を示すことではなく、CTMが連続的な活性化履歴の同期を活用して、LSTMと同等の性能を達成できることを示すことです。アーキテクチャと最適化ハイパーパラメータの詳細な説明は付録Iに記載されています。
CTMは継続的に世界と相互作用することができます。強化学習タスクの学習曲線を図27に示します。すべてのタスクにおいて、CTMはLSTMベースラインと同様のパフォーマンスを達成していることがわかります。
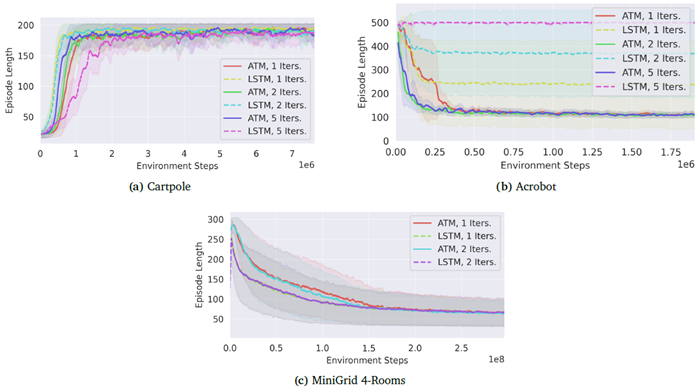
図27 | 強化学習タスクのトレーニング曲線。各曲線は、トレーニング中のエピソード長の移動平均を表し、3回のトレーニング実行の平均値です。網掛け部分はシード間の1標準偏差を表します。Cartpoleの場合、値が高いほど優れています。AcrobotとMiniGrid 4-roomsの場合、値が低いほど優れています。
図28は、CartPole、Acrobot、MiniGrid Four Roomsの各タスクにおけるCTMとLSTMベースラインのニューロントレースを比較したものです。従来の制御タスクでは、CTMとLSTMの両方の活性化は、カートとアームの前後運動に対応する振動的な挙動を示しています。ナビゲーションタスクでは、CTMに豊富で複雑な活性化パターンが現れます。一方、LSTMは活性化の多様性が低い傾向にあります。このセクションで学習したLSTMは、CIFAR-10で学習した場合(図12)よりも動的なニューロン活動を示します。これは、RLタスクのシーケンシャルな性質によるものと考えられます。RLタスクでは、モデルへの入力が環境との相互作用によって時間の経過とともに変化し、フィードバックループを引き起こし、モデルの潜在表現も時間の経過とともに進化します。

図28 | CartPole、Acrobot、MiniGridの「Four Rooms」タスクにおけるCTMとLSTMの単一エピソードにおける神経活動。CTMはLSTMよりも豊富なニューロンダイナミクスを備えています。
現代のニューラルネットワークは、様々な分野で目覚ましい成功を収めていますが、一般的には固定深度のフィードフォワード計算に依存しており、入力の複雑さに応じて処理を適応させる柔軟性は限られています。一方、生物の脳は、時間の経過とともに展開する動的な神経活動を示し、タスクの要求に合わせて計算を調整します。CTMは、この考え方に基づき、内部の神経タイミングと同期を明示的にモデル化します。本セクションでは、適応型計算、反復推論、そして生物学に着想を得たアーキテクチャに関連する主要な研究を取り上げます。これらはすべて、CTMの背後にある動機付けとなっています。
入力の難易度や信頼度に応じて推論ステップ数が変化する適応型計算は、これまで多くのアプローチで研究されてきました。早期終了ネットワーク(例:Bolukbasi et al. (2017))では、中間層が確信度の高い予測を生成した場合、モデルは推論を早期に終了できるため、簡単な例の計算時間を節約できます。PonderNet(Banino et al., 2021)は、再帰型モデルに確率的停止メカニズムを導入し、精度と効率性のバランスをとるエンドツーエンドの微分可能損失を通じて、入力ごとに学習された「熟考時間」を可能にしました。この手法は、アルゴリズム推論タスクにおいて、より安定したトレーニングとより強力な一般化を提供することで、適応型計算時間(ACT)(Graves, 2016)を改良しました。
最近では、AdaTape (Xue et al., 2023) が、入力を「テープトークン」で動的に拡張する柔軟なメモリ拡張アーキテクチャを提案しました。これにより、モデルは必要に応じてより多くの計算リソースを効率的に確保できます。同様に、Sparse Universal Transformer (SUT) (Tan et al., 2023) は、再帰的な重み共有と動的停止、およびMixture-of-Expertsルーティングを組み合わせることで、モデルが入力ごとに異なる数の再帰型Transformer層を適用できるようにしています。これらの手法は、入力依存計算の利点を示し、計算コストと問題の難易度を一致させます。これは、CTMが内部の「思考」次元を通じて追求している目標でもあります。
CTMは、反復推論と内部再帰向けに設計されたモデルと共通点を持っています。例えば、Quiet-STaR (Zelikman et al., 2024) は、学習中に隠れた根拠トークンを挿入することで言語モデルに「話す前に考える」ことを教え、出力生成前の内部計算を促します。このプロセスは、数学的推論や常識的な質疑応答といった複雑なタスクのパフォーマンスを向上させます。Recurrent Independent Mechanisms (RIMs) (Goyal et al., 2019) などの他のアーキテクチャは、計算をスパースに活性化されたモジュール型サブネットワークに分割し、時間の経過とともに非同期的に進化させることで、体系的な一般化と多段階推論を向上させます。これらのアプローチは、入力シーケンスに直接結び付けられていない内部の分離された計算を通じて思考をシミュレートするというCTMの目的を反映しています。
ニューラルコンピューティングをより生物学的に妥当なものにすることを目指す研究が増えています (Schmidgall et al., 2024)。Liquid Time-Constant Networks (LTCN) (Hasani et al., 2021) は、時間変動微分方程式に支配されるニューロンを用い、各ニューロンが入力履歴に基づいて動的に応答を適応させることを可能にします。これらのネットワークは、高いサンプル効率と堅牢性を備え、時間依存タスクにおいて優れた性能を示しています。同様に、スパイキングニューラルネットワーク (SNN) は、標準的なディープネットワークに代わる生物学的根拠に基づいた代替手段として注目を集めており、離散スパイクと正確なタイミングに基づいて情報を符号化および処理します。最近の進歩 (例: Stan and Rhodes (2024)) では、SNN を状態空間モデルおよび同期メカニズムと組み合わせることで、長距離シーケンスタスクにおいて競争力のある、あるいはそれ以上の性能を実現しています。
CTMは、そのような神経メカニズム、特に時間的符号化と神経同期から着想を得て、静的な活性化ではなく活動のタイミングに情報を符号化します。しかし、従来のモデルとは異なり、CTMはこれらのダイナミクスを注意と出力生成の潜在的表現として直接利用し、進化するニューロン状態の相互作用から推論が自然に生じる統一されたアーキテクチャを実現します。
本技術レポートでは、神経活動の時間的ダイナミクスをその知能の主要メカニズムとして展開し活用するモデルとしてCTMを紹介しました。私たちの知る限り、時間の経過に伴う神経同期をモデルの潜在的表現として用いることは、特にこの規模ではこれまで実現されていません。CTMは、自然認知において極めて重要であると考えられている時間的ダイナミクスの正確な相互作用とタイミングを用いて、多様なタスクを成功裏に実行するモデルの具体例であり、その証拠を本稿で示しました。
本研究の目的は、この新しいモデルと、ニューラルダイナミクスがニューラルコンピューティングの強力なツールとなり得るという視点を紹介することでした。研究コミュニティが本研究の一部を取り入れ、より生物学的に妥当で高性能なAIを構築してくれることを願っています。以下のサブセクションでは、私たちの観察に基づいた議論と展望をいくつか示します。
CTMの出力y𝑡は、同期からの線形射影として計算されます。例えば、y𝑡がクラス予測を表すオブジェクト分類を考えてみましょう。このシナリオでは、CTMは入力データ内の抽象的な特徴を観察し、ニューロン内に特定の活性化ダイナミクスを生成する必要があります。そして、これらの活性化ダイナミクスは、正確な予測を生成するために正確に同期する必要があります。直感的に言えば、これはCTMが入力データに応答して内部の刻み目を通して持続的な神経活動パターンを発達させることを学習し、時間的なプロセスを通じて効果的に出力を構築することを意味します。この概念は、最近の推論の概念と一致しており、私たちが「思考」という用語を選択した主な理由です。さらに、このような動的かつ時間的な表現は、標準的な表現を使用する既存の方法とは大きく対照的です。本論文の実験は、この種の表現の可能性を探る初期の段階ですが、生物学的プロセスとの類似性の高さから、最終的には大きな有用性を持つ可能性があることが示唆されています。
多重解像度:同期の測定は、時間経過に伴う活動に依存しますが、時間そのものに厳密に依存するわけではありません。これにより、同期の一部が時間の経過とともにゆっくりと変化する可能性があり、一方で、学習可能な時間依存性の減衰メカニズム(セクション2.4を参照)は、短期的な依存性の出現を可能にします。その結果、同期は、任意の数の解像度でイベントや視点を捉えることができる表現となります。多くの現実世界のシナリオでは、このような多重解像度の視点が強力になり得る特徴やアイデアが見られるため、今後の研究でこの点について検討します。
記憶 この点についてさらに言及すると、ある同期は、CTMのある期間における認知だけでなく、内部のティックの周期的な変化によって、CTMが行動をとった結果も捉えている。このような視点は、スナップショット表現よりもはるかに「経験」に近い。したがって、記憶としての同期行列は、今後の研究にとって興味深い道筋を示す。
可塑性と勾配フリー学習 本技術レポートで定義したように、同期とはニューロンがどのように同時に発火するかを測定するものであり、これは非常にヘブ的な視点です(Hebb, 2005; Najarro and Risi, 2020)。この概念を活用して生涯学習(Kudithipudi et al., 2022; Wang et al., 2024)、可塑性、さらには勾配フリー最適化を探求することは、今後の研究にとって刺激的な道筋です。
カーディナリティ 𝐷次元CTMにおける完全同期は(𝐷 × (𝐷 + 1))/2次元(完全同期行列の上三角)です。研究によると、大規模な表現はいくつかの理由から有利です(Allen-Zhu et al., 2019; Frankle and Carbin, 2018)。 同期により、追加コストなしで大規模で意味のある表現空間にアクセスできます。 私たちは、特にマルチモーダルモデリングの分野において、このような高カーディナリティの表現空間からどのような有用性が得られるかを探求するつもりです。
CTMの構築には自然界からヒントを得ましたが、学習には確立されたプロトコルとデータセットを使用しました。しかし、これらのデータセットとプロトコルは必ずしも自然なものではありません。例えば、従来のニューラルネットワークの学習では、独立かつ同一に分布するデータが期待されますが、現実世界ではそうではありません。イベントは時間の経過とともに発生し、通常はそれに応じて配置されます。したがって、将来の研究では、生物学的に妥当な方法でCTMを学習させることを目指しています。特に学習中に順番にサンプリングされたシーケンシャルデータ(例:動画、テキスト)への適用は、将来の研究にとって有望な道筋です。
言語モデリング CTMを言語モデリングのタスクに適用した例はまだありませんが、注意を利用するという点を踏まえると、テキストの取り込みと思考に適応させることは容易です。さらに、CTMは世界モデルを構築し、それをナビゲートできるため(セクション4を参照)、位置エンコーディングを必要とせず、観察対象の文脈化された「世界モデル」を構築できる可能性があります。読者の皆様にぜひご検討いただきたい潜在的な可能性の一つは、CTMを事前学習済みの言語モデルに適用することです。今後の研究では、テキストデータを用いてカスタムCTMを構築・学習し、その分野におけるCTMの能力を理解する予定です。
CTMの中核表現として当初何を試みたのか(同期表現ではなく)を説明することが重要だと考えています。活性化潜在空間z𝑡は明らかな候補です。しかし、Zの動的かつ複雑な性質から、何らかの平滑化操作(例えば、「ホルダー」潜在空間やロジットの蓄積など)を実行する必要があることがわかりました。さらに、この表現は𝑡と強く結合しているため、CTMは内部の自己組織化を主要な駆動力として頼るのではなく、出力を生成するタイミング(つまり、損失関数が適用されたタイミング)を正確に学習することがわかりました。
ニューロンのタイミングをシステムに組み込むことで、この課題が生じました。幸いなことに、時間に依存しない同期は、これらの課題を克服するための優れた解決策であることが証明されました。学習可能な減衰時間依存性は、CTMが短期的なニューロン行動に基づいて世界と相互作用することを学習するという、優れた解決策も提供します。
連続思考マシン(CTM)は、人工知能における計算効率と生物学的妥当性を橋渡しする新たな一歩です。従来の点単位の活性化関数からプライベートなニューロンレベルモデルへと移行することで、CTMははるかに豊かなニューロンダイナミクスを実現します。 重要なのは、ニューラルネットワークの初期から広く用いられてきた活性化ベクトルとは異なる、強力かつ根本的に新しいタイプの表現として、ニューラル同期を活用していることです。 ニューロンダイナミクスを第一級の表現要素として直接利用することで、CTMは現代のモデルとは質的に異なる動作を示すことができます。
私たちの研究は、このアプローチの具体的な利点を実証しています。CTMは、画像分類などのタスクにおいて、時間の経過とともに動的に表現を構築し、位置埋め込みなしに特定の入力データに注意を向けるための豊富な内部マップを形成し、自然に適応的な計算を行うことができます。さらに、CTMは神経ダイナミクスを同期させることで、直近の活動履歴を超えて記憶を保存・検索することを学習します。この内部処理は、迷路やパリティタスクを系統的に解くことに見られるように、より高い解釈可能性にも役立ちます。
驚くべきことに、CTMのコアアーキテクチャは、多様な難易度のタスクにおいてほぼ一貫性を保ち、入出力モジュールの調整のみを必要としました。この汎用性と学習可能性は、迷路ナビゲーションのような複雑なシナリオにおいて特に顕著でした。CTMは最小限のチューニングで成功を収めましたが、LSTMのような従来のモデルでは、大幅なチューニングを行った後でも依然として苦戦を強いられました。
この研究は、神経科学と機械学習の間にある、重要でありながらしばしば十分に探究されていない相乗効果を強調するものです。現代のAIは表面的には脳に着想を得ているように見えますが、この2つの分野はしばしば驚くほど孤立して機能しています。CTMは、生物学的原理からインスピレーションを得る力の証です。 このようなインスピレーションから出発し、出現する興味深い行動を反復的に追跡することで、私たちは、分類タスクにおける驚くほど強力なキャリブレーションなど、当初は想定されていなかった機能を備えたモデルを開発しました。
我々のアプローチは、厳密で文字通りの妥当性を追求するのではなく、生物学の概念を借用することを推奨していることに留意することが重要です。現実のニューロンはCTMでモデル化されたように活動履歴にアクセスできないかもしれませんが、それでも進行波のような創発現象は現れます。実用性と生物学的インスピレーションの間のこの微妙なバランスは、新たな研究方向への展望を開き、それが現在AIに欠けている能力を解き放つ鍵となる可能性があり、より人間に近い知性を示し、現在のAIの限界に対処するシステムにつながる可能性があります。
当初「なぜこの研究をするのか?」と自問したとき、CTMの旅が説得力のある答えを提供してくれることを期待していました。軽い生物学的インスピレーションを受け入れ、観察された新しい行動を追求することで、当初の設計を超える創発能力を備えたモデルに到達しました。私たちはこの探求を継続し、さらなる概念を借りて、どのような新しくエキサイティングな行動が生まれるかを発見し、AIの限界を押し広げていくことに尽力しています。
CTMの主な制限事項は、並列化できない逐次処理を必要とすることです。つまり、特に現代のAIモデルの現状は、並列開発されたハードウェアとソフトウェアに適していることを考慮すると、標準的なフィードフォワードモデルよりもトレーニング時間が長くなります(Hooker, 2021)。
ニューロンレベルモデルに関連する追加のパラメータコストも制約となる可能性があります。 メリットがコストを上回るかどうかはまだ証明されていませんが、その有用性は高いと考えています。
| 用語 | 説明 |
|---|---|
| 内部ティック | 内部計算の1ステップ。 |
| メモリ長 | ローリングFIFO方式で更新される、前活性化のローリング履歴の長さ。 |
| シナプスモデル | \(\mathbf z^𝑡\)と\(\mathbf o^𝑡\)を入力として受け取り、前活性化を予測する回帰モデル。\(\mathbf a^𝑡\)。 |
| 前活性化 | 回帰シナプスモデルの出力。NLMへの入力。 |
| 事後活性化 | NLMの出力、時刻 \(𝑡\) におけるニューロンの状態。 |
| (事前/事後)活性化履歴 | 時間経過に伴う活性化の順序付けられた履歴。 |
| ニューロンレベルモデル (NLM) | 事後活性化履歴に対するニューロンごとのMLP。 |
| 同期 | 事後活性化履歴のドット積。 |
| 自己ペア | 対角同期行列のエントリ \((𝑖,𝑖)\)。 |
| アクション同期 | アテンションクエリの同期表現。 |
| 出力同期 | 予測のための同期表現。 |
| 減衰 \(𝑟_{𝑖𝑗}\) | 同期(アクションまたは出力)のための学習可能な時間減衰。 |
| 特徴抽出器 | タスク固有の入力エンコーダ(例:ResNet)。 |
| アテンション出力 | アクション同期から計算されたクエリ、q𝑡、およびデータのキー/値を使用したクロスアテンション後の出力。 |
表 1 | 用語集
| シンボル | 意味 |
|---|---|
| \(𝑇\) | 内部ティック数 |
| \(𝑀\) | メモリ長 |
| \(𝑑_{model}\) | CTMにおける潜在状態の次元数 |
| \(𝑑_{input}\) | アテンション出力の次元数 |
| \(𝑑_{hidden}\) | 各ニューロンのプライベートMLP(NLM)における隠れニューロンのサイズ |
| \(𝑘\) | シナプスMLPまたはU-Netの深さ |
| \(𝑝_{dropout}\) | シナプスモデルにおけるドロップアウト確率 |
| \(𝑛_{heads}\) | マルチヘッドアテンションにおけるヘッド数 |
| \(𝐽_{action}\) | 動作同期に使用されるニューロン数 |
| \(𝐽_{out}\) | 出力同期に使用されるニューロン数 |
| \(𝐷_{action}\) | 動作同期の次元ベクトル |
| \(𝐷_{out}\) | 出力同期ベクトルの次元数 |
| \(𝑛_{self}\) | 同期サンプリングで使用される自己ペアの数 \((𝑖, 𝑖)\) |
| \(𝑟_{𝑖𝑗}\) | ニューロン𝑖と𝑗間の同期のための学習可能な減衰パラメータ |
| \(\mathbf S^𝑡\) | 内部ティックにおける完全な同期行列 \(𝑡\) |
| \(\mathbf q^𝑡\) | アクション同期から射影されたクエリベクトル |
| \(\mathbf y^𝑡\) | 出力同期から射影された出力ベクトル(例:ロジット) |
表 2 | 記号の用語集。
図29は、CTM内のニューロン間で情報を共有する再帰構造であるシナプスモデルを示しています。このモデルは、深さを𝑘(常に偶数)に設定することで実装されます。各層の幅は、幅16に達するまで次元を線形に削減し、その後はスキップ接続を用いて情報を保持しながら増加させます。シナプスモデルは、o𝑡(アテンションの出力)も入力として受け取ります。
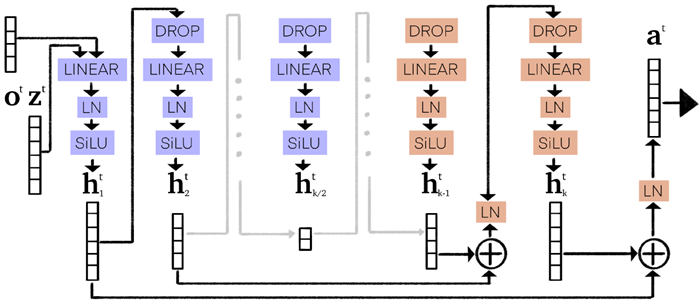
図29 | UNETスタイルの「シナプス」リカレントモデルの概要。z𝑡は前のステップからの事後活性化、o𝑡は観測データからのアテンション出力であり、シナプスモデルはNLMが処理するためのa𝑡の事前活性化を生成します。 UNET構造は、最内層のボトルネック層が16ユニット幅になるように設定され、その間の各層は線形スケーリングされます。層ノルムを持つスキップ接続は、情報を維持するために古典的なUNET構造を実装します。低次元を生成する層は青で示され、高次元を生成する層はオレンジで示されます。
218 / 5,000 CTMは、𝐷次元の潜在表現zに対して再帰性を用いて動作します。zは時間の経過とともに展開し、選択されたニューロン間の同期によって、CTMが実現する新しい種類の表現が形成されます。
ニューロンのペアは\(\frac{𝐷×(𝐷+1)}{2}\)個存在し、ニューロン同期ペアの集合はニューロン数よりもはるかに大きくなります。これが選択プロセスの必要性を生みます。 CTMの開発を通して、私たちはニューロンを選択するための3つのアプローチを考案しました。
このセクションでは、ImageNet-1K 実験の追加の詳細と結果について説明します。
このタスクでは、https://github.com/huyvnphan/PyTorch_CIFAR10 から改変した、古典的な ResNet アーキテクチャ (He et al., 2016) の制約版を使用しました。これは、ImageNet の標準実装とは異なり、最初の畳み込みでカーネルサイズが 7 × 7 ではなく 3 × 3 に制限されています。ResNet-152 構造を使用し、最終的な平均プーリングとクラスロジットへの射影を行う前の出力を取得しました。入力画像のサイズは 224 × 224 で、クロスアテンションで使用されるキーと値として 14 × 14 の特徴が生成されました。
次のハイパーパラメータを使用しました。
最適化には次の設定を使用しました。
リスト5は、ImageNet-1K上でCTMを学習するために使用した画像分類損失関数のPythonコードを示しています。これは、セクション2.5で定義された損失を伴います。
def image_classification_loss ( predictions , certainties , targets , use_most_certain = True ):
"""
Computes the maze loss with auto - extending cirriculum .
Predictions are of shape : (B, class , internal_ticks ),
Certainties are of shape : (B, 2, internal_ticks ),
where the inside dimension (2) is [ normalised_entropy , 1- normalised_entropy ]
Targets are of shape : [B]
use_most_certain will select either the most certain point or the final point .
"""
targets_expanded = torch . repeat_interleave ( targets . unsqueeze ( -1) , predictions . size ( -1), -1)
# Losses are of shape [B, internal_ticks ]
losses = nn. CrossEntropyLoss ( reduction ='none ')( predictions , targets_expanded )
loss_index_1 = losses . argmin ( dim =1)
loss_index_2 = certainties [: ,1]. argmax ( -1)
if not use_most_certain : # Revert to final loss if set
loss_index_2 [:] = -1
batch_indexer = torch . arange ( predictions . size (0) , device = predictions . device )
loss_minimum_ce = losses [ batch_indexer , loss_index_1 ]. mean ()
loss_selected = losses [ batch_indexer , loss_index_2 ]. mean ()
loss = ( loss_minimum_ce + loss_selected )/2
return loss
リスト 5 | ImageNet-1K で使用される、標準分類タスクのセクション 2.5 の損失関数の実装。
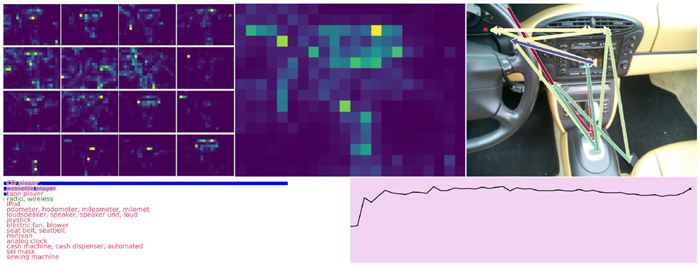
図 30 | 検証画像インデックス 1235。不正確で不確実な予測を示しています。
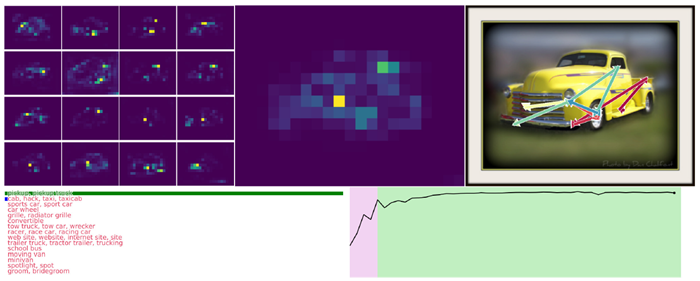
図 31 | 検証画像インデックス 15971。正しい予測と、妥当と思われる 2 番目に可能性の高いクラスを示しています。
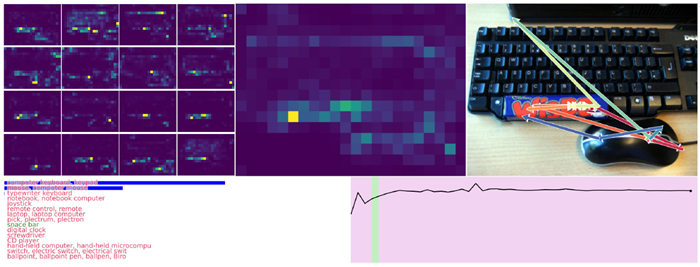
図 32 | 検証画像インデックス 21202、正しい予測を通り過ぎた後に誤った予測を示し、「考えすぎ」を示しています。
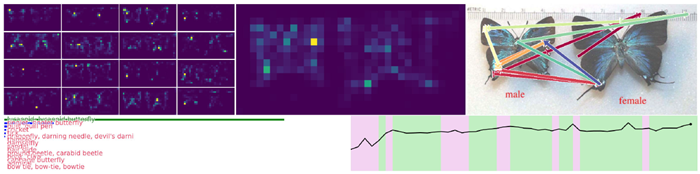
図 33 | 検証画像インデックス 39275、正しいが不確実な予測。
本研究では、maze-datasetリポジトリ(https://github.com/understanding-search/maze-dataset)を使用して迷路を作成しました。19×19、39×39、99×99のサイズの迷路を生成しました。
それぞれのケースで50,000個の迷路を生成し、45,000個の訓練セットと5,000個のテストセットに分割しました。本技術レポートでは、訓練には39×39のデータセットを使用し、一般化のテストには99×99のデータセットを使用しました。3つの迷路データセットはすべてCTMコードリポジトリで提供されています。8
8 19 × 19 はデバッグに有益であることがわかったため、これも提供しています。
次のハイパーパラメータを使用しました。
最適化には次の設定を使用しました。
その結果、31,998,330 個のパラメータを持つモデルが作成されました。
迷路を解くための損失関数にカリキュラム要素を組み込むように適応させました。式(12)の損失の𝑡1と𝑡2を計算する前に、まず各内部ティックにおける損失を変更し、迷路内の正しく予測されたステップと、経路に沿った追加の5ステップのみを考慮するようにしました。これにより、モデル(CTMまたはLSTMベースライン)は、迷路を最初から最後までゆっくりと解くことを効果的に学習できます。リスト6は、損失を計算する際にこれがどのように実装されているかを示しており、CTMとLSTMの両方のトレーニングに使用されます。
この課題を解決するために、いくつかのLSTMベースラインをテストしましたが、学習中の安定性に問題がありました(図7参照)。特に、LSTM層が1層を超える場合や、内部ティック数が多い場合が顕著でした。そこで、深度1、2、3の3つのLSTM構成をテストしました。各モデルについて、CTMと一致するように内部ティック数を75に設定し、安定性を確保するために内部ティック数を50に設定しました。また、平均プーリング前の特徴空間をCTMと同じ幅の隠れ層に投影するフィードフォワードモデルもテストしました。これにより、パラメータ数がわずかに増加しました。すべてのハイパーパラメータは一定に保ち、以下の設定を行いました。
def image_classification_loss ( predictions , certainties , targets , use_most_certain = True ):
"""
Computes the maze loss with auto - extending cirriculum .
Predictions are of shape : (B, class , internal_ticks ),
Certainties are of shape : (B, 2, internal_ticks ),
where the inside dimension (2) is [ normalised_entropy , 1- normalised_entropy ]
Targets are of shape : [B]
use_most_certain will select either the most certain point or the final point .
"""
targets_expanded = torch . repeat_interleave ( targets . unsqueeze ( -1) , predictions . size ( -1), -1)
# Losses are of shape [B, internal_ticks ]
losses = nn. CrossEntropyLoss ( reduction ='none ')( predictions , targets_expanded )
loss_index_1 = losses . argmin ( dim =1)
loss_index_2 = certainties [: ,1]. argmax ( -1)
if not use_most_certain : # Revert to final loss if set
loss_index_2 [:] = -1
batch_indexer = torch . arange ( predictions . size (0) , device = predictions . device )
loss_minimum_ce = losses [ batch_indexer , loss_index_1 ]. mean ()
loss_selected = losses [ batch_indexer , loss_index_2 ]. mean ()
loss = ( loss_minimum_ce + loss_selected )/2
return loss
リスト6 | 迷路経路予測のためのセクション2.5の損失関数の実装。CTMとLSTMの両方に対する自動カリキュラムアプローチを含む。
図34は、第4.1節の迷路解決モデルの損失曲線を示しており、このタスクで訓練した場合、CTMがより安定して高性能になることを示しています。
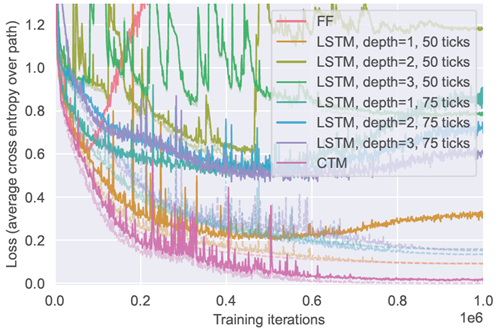
図 34 | CTM とベースラインをトレーニングするときの損失曲線。
制約付きResNet-18バックボーンの最初のハイパーブロック(付録C.1参照)を使用しました。畳み込み層は合計5層、ダウンサンプル係数は2倍です。CTMには以下のハイパーパラメータを使用しました。
最適化には次の設定を使用しました。
LSTMベースラインでは、単層LSTMよりも優れたパフォーマンスを示し、学習において比較的安定していた2層LSTMを使用しました(迷路タスクと比較して)。CTMのシナプス深度、メモリ長、NLM隠れ層の幅は、モデル幅が一定(256)になるように選択し、CTMとLSTMのパラメータ数はほぼ一致するようにしました。フィードフォワードモデルでは、モデル幅を一定に保ちました。
このセクションでは、CIFAR-100 実験の詳細について説明します。
セクション6.1では、制約付きResNet-34バックボーンの最初の2つのハイパーブロック(付録C.1参照)を使用しました。ダウンサンプル係数は4倍です。この実験では、𝐷を変化させましたが、その他のハイパーパラメータは以下のように設定しました。
セクション6.2では、制約付きResNet-19バックボーンの最初の2つのハイパーブロック(付録C.1参照)を使用しました。ダウンサンプル係数は4倍です。この実験では、𝑇を変化させましたが、その他のハイパーパラメータは以下のように変更しませんでした。
このモデルは、より多くのティックを使用することで生じるオーバーヘッドのため、他のCIFAR-100アブレーションと比較してより制約が厳しく設定されています。セクション6.2で説明したように、より長いティックで学習された変異体は、より多くの学習から利益を得る可能性があり、この実験でより大きなモデルを使用する場合、この差異はさらに大きくなります。
パリティタスクの入力データは長さ64のベクトルで、各位置は-1または1です。 各サンプルのターゲットは同じサイズのベクトルで、各位置はその位置までのシーケンスのパリティ(累積パリティ)です。このデータは、新しいバッチがフェッチされるたびにオンザフライで生成されます。
パリティタスクの実験では、以下のアーキテクチャが用いられる。モデルへの入力は(𝐵, 64)の形状であり、ミニバッチのサイズとシーケンスの長さはそれぞれ𝐵と64である。長さ64のシーケンスの各値は、ランダムに-1または1となる。まず、-1と1の値は𝑑embed = 𝑑inputの埋め込みに変換され、位置埋め込みが加算される。得られた埋め込みは、層正規化を伴う線形層に渡され、(同一の)アテンションキーとアテンション値が形成される。第2節で説明したように、𝐽actionニューロン間の同期が計算され、この表現からアテンションクエリが形成される。このクエリは、アテンション値の計算に使用され、アテンション値は活性化状態に連結され、シナプスとニューロンレベルモデルによって処理される。シナプスには、浅いフィードフォワードネットワークを使用します。このプロセスは𝑇内部ティックごとに繰り返され、各内部ティック𝑡において、𝐽outニューロン間の同期が計算され、ロジット空間に投影されます。
パリティタスクでは、内部ティック数とメモリ長を変化させた場合のモデルのパフォーマンスを実験しました。ベースラインとして、CTMと同じ内部ティック数を使用し、パラメータマッチングされた単層LSTMを使用しました。すべてのCTMモデルは、以下に示す共通のアーキテクチャハイパーパラメータセットを共有しています。表3は、実験構成によって異なるハイパーパラメータのサブセットを示しています。
| Model | 𝑇 | 𝑀 | \(𝑑_{model}\) | Total Parameters |
|---|---|---|---|---|
| CTM | 1 | 1 | 1024 | 4908706 |
| LSTM | 1 | - | 669 | 4912710 |
| CTM | 10 | 5 | 1024 | 5043874 |
| LSTM | 10 | - | 686 | 5050716 |
| CTM | 25 | 10 | 1024 | 5212834 |
| LSTM | 25 | - | 706 | 5224386 |
| CTM | 50 | 25 | 1024 | 5719714 |
| LSTM | 50 | - | 765 | 5722374 |
| CTM | 75 | 25 | 1024 | 5719714 |
| LSTM | 75 | - | 765 | 5722374 |
| CTM | 100 | 50 | 1024 | 6564514 |
| LSTM | 100 | - | 857 | 6567486 |
表 3 | パリティ タスクのモデル ハイパーパラメータ (構成によって異なります)。
CTMはセクション2.5で説明した確実性ベースの損失関数を用いて学習されましたが、LSTMベースラインは最終内部ティックで計算されたクロスエントロピー損失を利用しました。この選択は、確実性ベースの損失関数を用いてLSTMを効果的に学習させることが当初困難であったために行われました。図35は、最終損失または確実性ベースの損失を用いて学習した、10回および25回の反復回数におけるLSTMベースラインの学習精度曲線を比較しています。一般的に、複数の内部ティックを持つLSTMの場合、どちらの損失関数も学習が不安定になります。
最適化には次の設定を使用しました。
モデルのパフォーマンスはシード間で大きく異なります。図19は、様々なCTMおよびLSTM構成におけるトレーニング中の精度を示しています。各構成は3回の独立した実行の平均値です。これらのトレーニング曲線は、実行間でパフォーマンスが大きく異なるため、かなりのばらつきを示しています。これは、初期のランダムシードに強く影響されます。例えば、図36は、75の内部ティックと25のメモリ長でトレーニングされたCTMの個々のトレーニング曲線を示しています。実行1と3は完璧な精度に達していますが、実行2は準最適な解に収束しています。
さらに、これら3つのモデルはすべて著しく異なる挙動を示し、各CTMは75の内部ティックにわたって入力シーケンスの非常に異なる部分に注意を払います。内部ティックにおけるこれらの注意パターンは図37に示されています。実行3では、シーケンス全体の最初から最後まで注意を払うモデルが生成されますが、実行1では逆の順序で注意を払います。
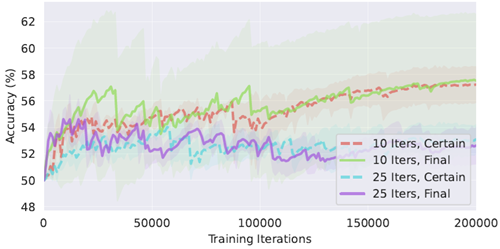
図35 | 最終内部ティックにおける確実性ベースの損失またはクロスエントロピー損失のいずれかで学習したLSTMベースラインのテスト精度。どちらの損失関数も学習が不安定になる。
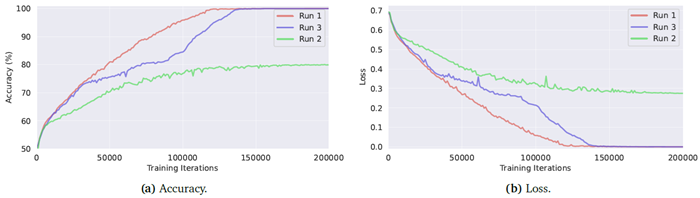
図36 | 3つのランダムシードを用いて学習した3つのCTMの学習曲線。実行1と3は損失がゼロに収束しますが、もう1つの実行は損失がゼロ以外になります。
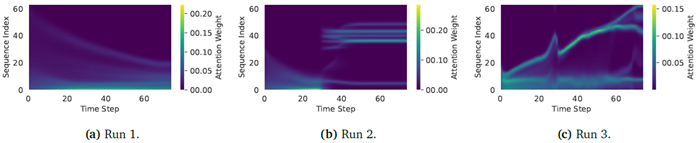
図 37 | トレーニング後の 3 回の実行ごとの注意パターン。
他のタスクとは異なり、Q&A MNISTタスクは、MNIST数字画像、演算子とインデックスマーカーの埋め込み、そして回答フラグとしてのゼロテンソルなど、複数の入力タイプを処理します。MNIST画像は、2つの畳み込みブロック(各ブロックは畳み込み層、バッチ正規化、ReLU活性化、および最大プーリング層を含む)で構成される畳み込みバックボーンによる前処理を受けます。このバックボーンからの出力はアテンションキーとアテンション値を形成し、CTMは同期表現からの射影を用いてこれらを照会します。結果として得られるアテンション出力は、シナプス処理の前にCTMのアクティブ状態と連結されます。対照的に、演算子とインデックスの埋め込み、そして回答フラグは、畳み込みバックボーンとアテンションメカニズムをバイパスし、CTMのアクティブ状態に直接連結されます。演算子は学習された埋め込みを使用し、インデックスは正弦波埋め込み(Vaswani et al., 2017)を利用し、回答フラグは埋め込み次元に一致するゼロベクトルです。
比較のために、パラメータと内部ティックが一致した単層LSTMベースラインを使用しました。実験で使用した共通パラメータは以下のとおりです。
| Model | 𝑇 | 𝑀 | Repeats/Input | Answering Steps | Total Parameters |
|---|---|---|---|---|---|
| CTM | 1 | 3 | 1 | 1 | 2,501,388 |
| LSTM | 1 | - | 1 | 1 | 2,507,218 |
| CTM | 10 | 30 | 10 | 10 | 3,413,772 |
| LSTM | 10 | - | 10 | 10 | 3,418,954 |
表4 | Q&A MNIST実験における異なるモデルのハイパーパラメータと合計パラメータ。Repeats/Input列は、モデルが一意の入力を処理するために使用した内部ティック数を示します。例えば、Repeats/Input = 10は、MNISTの各数字と各インデックスまたは演算子の埋め込みを処理するために10内部ティックが使用されることを意味します。Answering Stepsは、回答フラグが観測される内部ティック数を示します。
CTMはセクション2.5で説明した確実性ベースの損失関数を用いて学習され、LSTMベースラインは最終内部ティックにおけるクロスエントロピー損失を用いて学習されました。最適化には以下の設定を使用しました。
CartPole CartPoleタスク(CartPole-v1)は、強化学習における古典的なタスクです。摩擦のない軌道上を移動するカートにヒンジで接続されたポールのバランスをとるタスクです。システムは、ポールを垂直に保つことを目的として、カートに水平方向の力(左または右)を加えることで制御されます。1歩ごとに+1の報酬が与えられ、ポールの角度が±12◦を超えるか、カートの位置が±2.4を超えるか、エピソードの長さが最大歩数(200歩に設定)を超えるとエピソードは終了します。さらに、報酬の正規化を使用して、即時報酬の指数移動平均がほぼ一定の分散を持つようにします。
行動空間は、カートに作用する力の方向に対応する2つの離散的な行動から構成されます。典型的なカートポール課題では、観測空間は(4, )の形状を持ち、値はカートの位置、カートの速度、ポールの角度、ポールの角速度に対応します。しかし、CTMを用いた本実験では、環境を部分的に観測可能にするために、カートの速度とポールの角速度はマスクされています。
Acrobot Acrobotタスク(Acrobot-v1)では、2つのリンクが直線的に接続されたチェーンで構成されるシステムが用いられ、チェーンの一端は固定されています。2つのリンク間のジョイントは駆動され、固定端のジョイントは自由に回転します。目標は、駆動ジョイントにトルクを加えて、チェーンの自由端をできるだけ少ないステップ数で特定の高さ以上に振り上げることです。チェーンは最初はランダムな角度と速度で垂れ下がっています。エピソードは、チェーンが必要な高さを超えるか、最大ステップ数(500ステップに設定)に達した時点で終了します。目標到達までのすべてのステップに対して-1の報酬が発生し、上限は-100です。
動作空間は3つの離散動作から構成され、駆動関節に-1、0、1𝑁𝑚のトルクをかける。観測空間は(6)の形状で、第1関節のなす角度の正弦と余弦(角度0は第1リンクが真下を向いていることを示す)、第2リンクの正弦と余弦(角度0は2つのリンク間の角度が同じであることを示す)、そして2つの角度の角速度から構成される。CartPoleタスクと同様に、これら2つの角速度成分はマスクされているため、環境は部分的にしか観測できない。
ミニグリッド 4 つの部屋 ミニグリッド 4 つの部屋タスク (MiniGrid-FourRooms-v0) は、エージェントが壁の 4 つの隙間で相互接続された 4 つの部屋で構成されたグリッドワールド内を移動する必要がある強化学習環境です。エージェントは、緑色の四角にあるゴールに到達した場合は 1 − 0.9 (歩数×最大歩数) の報酬を、それ以外の場合は 0 を受け取ります。ここでも、報酬正規化を使用して、過去の報酬の移動平均を正規化します。エージェントの位置、ゴールの位置、および壁の 4 つの隙間は、各エピソードの開始時にランダムに配置されます。環境は、エージェントがゴールに到達するか、最大歩数 (300 歩に設定) に達したときに終了します。
アクション空間は、左折、右折、前進、拾う、落とす、切り替え、完了に対応する7つの個別のアクションで構成されています。これらのアクションのうち、最初の3つだけがタスクに関連し、残りの4つのアクションは待機または何もしないアクションとして動作します。このタスクでは、エージェントの視野は限られており、エージェントの前方にある7×7のグリッドで構成されています。この環境の観測空間は7×7×3の形状で、7×7のタイルのそれぞれは、その位置にあるオブジェクト、色、状態IDに対応する3次元タプルとしてエンコードされています。具体的には、11種類のオブジェクト(壁、床など)、6種類の色、3種類の状態(開いている、閉じているなど)があります。
PPOを用いた学習のためのCTMの構成は以下のとおりです。まず、観測データはフィードフォワードネットワークなどのバックボーンによって処理され、アテンション機構を介さずにCTMの現在のアクティブ状態に連結され、一定数の内部ティックにわたって処理されます。この一定数の内部ティックの後、出力ニューロン間の同期が計算され、アクターヘッドとクリティックヘッドに渡され、次のアクションの選択と状態値の推定が行われます。
活性化履歴全体にわたって同期を計算する他のタスクとは異なり、RL 設定ではメモリ長 𝑀 のスライディングウィンドウを使用します。このアプローチにより、これらのタスクでは数千にまで達する可能性のある非常に長い活性化履歴の蓄積を防止できます。さらに、これにより、エピソードの展開の全段階で同じ形状のテンソルを維持できます。これを実現するために、CTM は学習済み初期状態トレースと学習済み初期活性化状態トレースの両方で初期化され、各エピソードの初期化時にモデルに提供されます。モデルの 1 回のフォワードパス(1 つの環境ステップに対応)の後、これらの状態トレースは維持され、次の環境ステップでモデルに提供されます。これにより、CTM は継続的な活動履歴を処理できるため、過去の多くの環境状態からの活性化が現在に影響を与えることができます。
従来の制御タスクでは、観測バックボーンは線形層、ゲート線形ユニット(GLU)(Dauphin et al., 2017)、および層の正規化を含む2つのブロックで構成されています。ナビゲーションタスクでも同様の入力処理が行われますが、オブジェクト、色、状態IDのそれぞれが最初に𝑑𝑒𝑚𝑏𝑒𝑑 = 8に埋め込まれます。CTMの場合、バックボーンの出力は現在のアクティブ状態に連結されますが、LSTMベースラインの場合、出力はCTMと同じ数の内部ティックで処理されます。アクターヘッドとクリティックヘッドは、それぞれReLU活性化を持つ64個のニューロンからなる2層の多層パーセプトロン(MLP)として実装されています。 CTMの場合、これらのヘッドは出力ニューロンの同期を入力として受け取りますが、LSTMベースラインの場合、これらのヘッドはLSTMの隠れ状態を𝑇内部ティック後に受け取ります。同期させるニューロンを選択するために、密なペアリングが使用されました。
画像分類(セクション3)などのUNetスタイルのシナプスモデルを使用する他のタスクとは異なり、RLタスクでは2層のフィードフォワードシナプスを採用しています。各層は線形変換、GLU、LayerNormで構成されています。経験的に、これらの2層は単層シナプスよりも大幅に優れた性能を発揮することがわかりました。特にナビゲーションタスクでは、単層シナプスではLSTMの平均エピソード長に一貫して一致しませんでした。
CartPole、Acrobot、MiniGrid Four Roomsの実験に使用されたモデルのハイパーパラメータは、表5~7に記載されています。
| Model | 𝑇 | 𝑀 | \(𝑑_{model}\) | \(𝑑_{input}\) | \(𝑑_{hidden}\) | \(𝑱_{out}\) | Total Parameters |
|---|---|---|---|---|---|---|---|
| CTM | 1 | 10 | 128 | 128 | 4 | 16 | 175437 |
| LSTM | 1 | – | 118 | 128 | – | – | 175855 |
| CTM | 2 | 20 | 128 | 128 | 4 | 16 | 188237 |
| LSTM | 2 | – | 126 | 128 | – | – | 188863 |
| CTM | 5 | 50 | 128 | 128 | 4 | 16 | 226637 |
| LSTM | 5 | – | 148 | 128 | – | – | 227275 |
表 5 | CartPole 実験のモデルハイパーパラメータ。
| Model | 𝑇 | 𝑀 | \(𝑑_{model}\) | \(𝑑_{input}\) | \(𝑑_{hidden}\) | \(𝑱_{out}\) | Total Parameters |
|---|---|---|---|---|---|---|---|
| CTM | 1 | 5 | 256 | 64 | 4 | 16 | 350094 |
| LSTM | 1 | – | 243 | 64 | – | – | 350118 |
| CTM | 2 | 10 | 256 | 64 | 4 | 16 | 362894 |
| LSTM | 2 | – | 249 | 64 | – | – | 364290 |
| CTM | 5 | 25 | 256 | 64 | 4 | 16 | 401294 |
| LSTM | 5 | – | 265 | 64 | – | – | 403490 |
表 6 | Acrobot 実験のモデルハイパーパラメータ。
| Model | 𝑇 | 𝑀 | \(𝑑_{model}\) | \(𝑑_{input}\) | \(𝑑_{hidden}\) | \(𝑱_{out}\) | Total Parameters |
|---|---|---|---|---|---|---|---|
| CTM | 1 | 10 | 512 | 128 | 16 | 32 | 7802690 |
| LSTM | 1 | – | 294 | 128 | – | – | 7813692 |
| CTM | 2 | 20 | 512 | 128 | 16 | 32 | 7976770 |
| LSTM | 2 | – | 300 | 128 | – | – | 7979304 |
表 7 | MiniGrid Four Rooms 実験のモデルハイパーパラメータ。
モデルは、単一のH100 Nvidia GPU上でProximal Policy Optimization (Schulman et al., 2017)を用いて学習されました。CTMとLSTMベースラインの両方に同じPPOハイパーパラメータセットが使用されており、表8に示されています。
| Hyperparameter | CartPole | Acrobot | MiniGrid Four Rooms |
|---|---|---|---|
| Learning Rate (LR) | \(1×10^{−3}\) | \(5 × 10^{−4}\) | \(1 × 10^{−4}\) |
| Total Environment Steps | 10M | 2M | 300M |
| Rollout Length | 50 | 100 | 50 |
| Number of Environments | 256 | 12 | 256 |
| Max Environment Steps per Episode | 200 | 500 | 300 |
| Update Epochs | 4 | 1 | 1 |
| Minibatches | 4 | 4 | 4 |
| Discount Factor (𝛾) | 0.99 | 0.99 | 0.99 |
| GAE Lambda (𝜆) | 0.95 | 0.95 | 0.95 |
| Clip Coefficient | 0.1 | 0.1 | 0.1 |
| Entropy Coefficient | 0.1 | 0.1 | 0.1 |
| Value Function Coefficient | 0.25 | 0.25 | 0.25 |
| Value Function Clipping | No | No | No |
| Max Gradient Norm | 0.5 | 0.5 | 0.5 |
表 8 | 各タスクの PPO ハイパーパラメータ。
図6の構築にはUMAP (McInnes et al., 2018) を使用しました。この場合のUMAPの目的は、ImageNet CTM内の各ニューロンに2次元的な位置を与え、ニューロンの活動の経時変化を視覚化する際に、意味のあるパターンが存在する場合にそれを観察できるようにすることです。この目的のために、200枚の異なる画像における活動後の履歴をUMAPへの高次元入力(200 × 𝑇 = 200 × 5 = 1000次元)として考慮しました。そして、UMAPを用いてこれを2次元空間に投影し、視覚化しました。
In Section 2.4 we defined the synchronization matrix at internal tick 𝑡 as \[ \mathbf S^𝑡 = \mathbf Z^𝑡 (\mathbf Z^𝑡)^⊺, \mathbf Z^𝑡 ∈\mathbb ℝ^{𝐷×𝑡} \tag{13} \] ここで、\(\mathbf Z^𝑡\) の n 番目の行には、ニューロン 𝑑 のティック \(𝑡\) までの活性化後のトレースが格納されます (式 (4) を参照)。式 (13) はティックごとにすべての 𝐷2 内積を最初から再計算するため、その時間計算量は長さ 𝑡 のロールアウト全体で O(𝐷2𝑡) です。以下では、式 (10) を指数関数的に減少させる再スケーリングにより、ティックごとに O(𝐷sub) の作業しか必要としない 1 階の再帰のペアから同じ量を取得できることを示します。ここで、𝐷sub ≪ 𝐷 は、出力とアクションの投影に実際に使用されるサブサンプリングされたニューロンインデックスの数です。
表記を明瞭にするため、まず単一の(𝑖,𝑗)ニューロンペアを考え、サブサンプリングは省略する。ペアのバッチへの拡張は即座に可能である。再スケールされた同期エントリは次のように定義されることを思い出してほしい。 \[ 𝑆_{ij}^𝑡 =\frac{\sum\limits_{𝜏=1}^t e^{−𝑟_{𝑖𝑗} (𝑡−𝜏)} 𝑧_i^𝜏 𝑧_j^𝜏}{\sqrt{\sum\limits_{\tau=1}^t e^{−𝑟_{𝑖𝑗} (𝑡−𝜏)}}} \tag{14} \] ここで、\(𝑟_{𝑖𝑗} ≥ 0\) はペア (𝑖, 𝑗) の学習可能な減衰率である。以下の補助シーケンスを定義する。 \[ \begin{align} \alpha_{ij}^t &:= \sum_{\tau=1}^t e^{-r_{ij}(t^tau)}z_i^\tau z_j^\tau \alpha_{ij}^1=z_i^1z_j^1 \tag{15} \\ \\ \beta_{ij}^t &:= \sum_{𝜏=1}^t e^{−𝑟_{𝑖𝑗} (𝑡−𝜏)} \beta_{ij}^1=1 \tag{16} \end{align} \] すると、\(𝑆_{ij}^𝑡 = 𝛼_{ij}^𝑡/\sqrt{𝛽_{ij}^𝑡}\) となり、\(𝛼_{ij}^𝑡\) と \(𝛽_{ij}^𝑡\) は両方とも単純な1階差分方程式に従います。 \[ \begin{align} 𝛼_{ij}^{𝑡+1} &= e^{−𝑟_{𝑖𝑗}}𝛼_{ij}^𝑡 + 𝑧_i^{𝑡+1}𝑧_j^{𝑡+1} \tag{17} \\ \\ 𝛽_{ij}^{𝑡+1} &= e^{−𝑟_{𝑖𝑗}} 𝛽_{ij}^𝑡 + 1 \tag{18} \end{align} \] 式(17)のランク1更新により、完全な活性化履歴を保存したり、大きな外積を繰り返し形成したりする必要がなくなる。順方向シミュレーション中、選択された各ペアについて \(𝛼_{ij}^𝑡\) と \(𝛽_{ij}^𝑡\) を維持し、\(\mathcal O(1)\) 時間で更新する。
実際には、\(\{𝛼_{ij}^𝑡, 𝛽_{ij}^𝑡\}\) は、\(\mathbf S_{out}^𝑡\) と \(\mathbf S_{action}^𝑡\) を形成する2つの互いに素な部分サンプルに対してのみ保存されます (セクション 2.4)。したがって、メモリ使用量と計算オーバーヘッドはどちらも保持されるペアの数に比例して増加します。つまり、ティックあたり \(\mathcal O(𝐷_{sub}) = \mathcal O(𝐷_{out} + 𝐷_{action})\) となります。