UniK3D

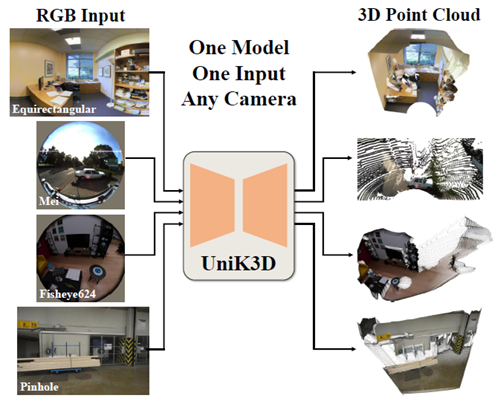
単眼3D推定は視覚認識にとって極めて重要です。しかしながら、現在の手法は、ピンホールカメラモデルや補正画像といった過度に単純化された仮定に依存しているため、不十分です。これらの制限により、汎用性が大幅に制限され、魚眼レンズやパノラマ画像を用いた現実世界のシナリオでは性能が低下し、コンテキストの大幅な損失につながります。この問題を解決するため、我々は、あらゆるカメラをモデル化できる、単眼3D推定のための初めての汎用化手法であるUniK3D1を紹介します。この手法は、球面3D表現を導入することで、カメラとシーンの形状をより適切に分離し、制約のないカメラモデルに対して正確なメトリック3D再構成を可能にします。このカメラコンポーネントは、球面調和関数の学習された重ね合わせによって実現される、モデルに依存しない新しい光線束表現を特徴としています。また、カメラモジュールの設計と相まって、広視野カメラの3D出力の縮小を防ぐ角度損失も導入しました。 13種類の多様なデータセットを用いた包括的なゼロショット評価により、3D、深度、カメラメトリクスにおけるUniK3Dの最先端の性能が実証されました。従来のピンホールによる小視野領域では最高の精度を維持しながら、困難な広視野角やパノラマ撮影において大幅な性能向上が見られました。コードとモデルはgithub.com/lpiccinelli-eth/unik3dで入手できます。

1. はじめに

3Dシーンの形状推定は、コンピュータビジョンにおける基本的なタスクです。なぜなら、そのような3D情報は、行動計画と実行のための重要な手がかりとなるからです[14, 89]。シーンの3D形状推定タスクは、正確な空間理解が不可欠な、自律航法[56, 76]や3Dモデリング[13]など、幅広いアプリケーションにとって不可欠です。一般化可能な単眼深度推定(MDE)[32, 63, 81]の最近の進歩は、様々な領域で優れた性能と視覚品質をもたらしますが、これらのモデルは相対的な出力スケールに制限されています。それでもなお、実用的なアプリケーションでは、一貫性と信頼性のあるメトリックスケールの単眼深度推定(MMDE)が不可欠です。これは、具現化されたエージェントに必要な正確な3D再構築とシーンの形状理解を可能にするためです。

既存の手法は、上記のメトリック推定の方向において大きな進歩を遂げてきました。初期のアプローチでは、テスト時にカメラの内部情報が既知であると仮定していました [24, 85]。一方、最近の研究ではこの仮定が緩和されています [9, 60, 61]。しかし、これらのアプローチは、入力カメラに関して依然として制限的な仮定を課しており、例えば、基本的なピンホールカメラモデルに依存すること [9, 60]、または正解補正パラメータへのアクセスを必要とすること [85] などが挙げられます。これらの単純化は、魚眼レンズやパノラマレンズなど、強い非線形変形を伴う様々なカメラ投影モデルが一般的である現実世界の設定において、上記の手法の適用性を大幅に阻害し、性能を低下させます。この制限は、深度マップのみではなく完全なメトリック3Dジオメトリを推定する場合により顕著になります。これは、前者がカメラ推定の品質に大きく依存するためです。既存モデルにおける制約的な仮定のため、様々な種類のカメラからの画像を用いてモデルを学習したとしても、一般的なカメラ推定を効果的に学習することができません。さらに、従来の最先端のMMDE法の出力空間には固有の限界があり、例えば、視野角（FoV）が180度を超えると、視差予測と対数深度予測はどちらも数学的に不良設定となります。

これらの課題に対処するため、我々は、図1に示すように、ピンホールから魚眼レンズ、パノラマ構成まで、幅広いカメラモデルに一般化できる、単眼メトリック3Dシーンの形状推定のための初のフレームワークであるUniK3Dを導入する。我々の手法は、2つの意味で球面的な単眼3D推定のための新しい定式化を提案する。第一に、UniK3Dは完全に球面の出力3D空間を活用し、垂直深度ではなく放射距離で範囲次元をモデル化する。このアプローチは、光軸からの角度が大きい場合に特に有益であり、極端な視野における従来の方法の不適正性を効果的に解決する。第二に、最近提案されたカメラ予測と深度推定の分解[60]に基づき、UniK3Dは光線束を表すカメラモジュールの直接出力空間として、一般的な球面調和関数基底を新たに提示する。先行研究 [9, 60] では、ピンホールカメラのパラメータを明示的に予測し、球面基底を用いて誘導光線を符号化していましたが [60]、本研究ではカメラの仮定を排除し、光線を直接モデル化します。その結果、UniK3D はカメラモデルの可能な範囲を無制限に拡張し、カメラの固有値に関わらず、柔軟かつ正確な深度予測を可能にします。本研究の仮定フリーの球面カメラ表現は、その柔軟性により、非標準カメラでシーンを撮影することが一般的である現実世界での展開に本モデルが適していることを保証します。

図1. UniK3Dは、カメラ情報を必要とせずに、ピンホールからパノラマまで、あらゆるタイプのカメラで、単一の画像から正確なメトリック3Dジオメトリ推定を実現する、斬新で汎用的なアプローチを導入します。(i) 3D空間の半径方向とカメラモデルに依存する2つの方向方向の両方に対する柔軟で汎用的な球面定式化と、(ii) 高度な調整戦略を活用することで、UniK3Dはカメラのキャリブレーションやドメイン固有のチューニングを必要とせずに、従来のモデルよりも優れた性能を発揮します。

私たちの主要な貢献は、あらゆるカメラの射影幾何学に対応できる、単眼3D推定のための初のカメラユニバーサルモデルです。これは、すべての逆射影問題をサポートする統一された球面出力表現によって実現されます。完全な球面フレームワークを採用することで、私たちの手法は射影と3Dシーン幾何学の完全な分離を保証します。これは、画像上の物体投影の次元が、深度ではなく半径距離に関してのみ一義的な関数であるためです。この分離により、より一貫性のある3D再構成が可能になり、深度がゼロに近づくxy平面付近での3D出力の安定性が向上します。さらに、UniK3Dはカメラ光線を有限の球面調和関数基底にわたる分解としてモデル化します。この選択により、表現の一般性と汎用性が確保されると同時に、結果として得られる光線束の正確かつコンパクトな表現が維持され、連続性や微分可能性といった帰納的バイアスも導入されます。さらに、我々は、四分位回帰に基づく非対称角度損失、静的エンコーディング、カリキュラム学習など、ラジアルモジュールの堅牢なカメラコンディショニングを確保するための複数の新しい戦略を提案します。

我々は、広く使用されている13のメトリック深度データセットを用いた広範なゼロショット実験を通じて、このアプローチを検証しました。UniK3Dは、単眼メトリック深度と3D推定において最先端の性能を達成するだけでなく、トレーニング中に前処理や特定のカメラドメインを使用することなく、さまざまなカメラモデルにわたって非常に優れた一般化を実現します。

2. 関連研究

単眼深度推定。[16] によって初めて実証されたMDEのためのエンドツーエンドニューラルネットワークの導入は、スケール不変対数損失 (SIlog) を用いた直接最適化による深度予測を可能にし、この分野に革命をもたらしました。それ以来、この分野は、畳み込みアーキテクチャ [19, 36, 45, 58] から、トランスフォーマーを使用した最近の進歩 [6, 59, 80, 86] に至るまで、ますます洗練されたモデルによって進化してきました。これらのアプローチは、制御されたベンチマークにおけるMDE性能の限界を押し広げてきましたが、ゼロショットシナリオに直面したときにしばしば失敗し、さまざまなカメラやシーン領域、そして多様な幾何学的条件や視覚条件にわたって堅牢な一般化を保証するという永続的な課題を浮き彫りにしています。一般化可能な単眼深度推定。ドメイン固有モデルの限界に対処するため、最近の研究では、一般化可能なゼロショットMDE手法の開発に焦点が当てられています。これらの手法は、スケールの曖昧さを軽減し、知覚的な奥行き品質を重視することを目的とするスケール非依存アプローチ [32, 63, 73, 81, 82] と、正確な幾何学的再構成を優先するメトリック奥行きモデル [7, 9, 24, 28, 60, 61, 85] に分類できます。しかし、既存のMDE手法のほとんどは、真のゼロショット単眼メトリック3Dシーン推定を実現できていません。特に、スケール非依存アプローチでは、スケールの曖昧さを解決するために追加の情報が必要になることが多く、メトリックベースのモデルのほとんどは、既知のカメラに依存するか、単純なピンホールカメラ構成を前提としています。ゼロショット3Dシーン推定用に設計された少数のモデルでさえも制約を受けます。これらのモデルは、ピンホールカメラモデルを明示的に仮定するか[9, 60]、画像の平行化を必要とするかのいずれかであり[85]、実質的にはテスト時のカメラ情報が必要となり、ゼロショットの一般化はピンホールカメラに限定されます。

一方、UniK3Dは、あらゆる逆投影問題に対応できる統合ソリューションを提供することで、これらの制限に対処します。このモデルは、カメラの固有パラメータに関わらず、テスト時に補正やカメラ情報を入力する必要なく、任意の単一画像からコヒーレントな3D点群を復元できます。この汎用性こそがUniK3Dの特徴であり、多様で困難な実世界アプリケーションで必要とされる、堅牢で汎用的な単眼メトリック3D推定を可能にします。カメラキャリブレーション。カメラキャリブレーションは、焦点距離、主点、歪み係数などの固有パラメータを推定し、3Dワールドポイントから2D画像座標へのマッピングをモデル化するために不可欠です。ピンホールモデル、Kannala-Brandtモデル[30]、Meiモデル[49]、Omnidirectionモデル[64]、Unified Camera Model (UCM) [22]、Enhanced UCM [33]、Double Sphereモデル[69]などの従来のパラメトリックモデルは、狭角レンズと広角レンズの両方に有効ですが、正確なキャリブレーションには制御された環境が必要です。モデルが複雑になるにつれて、特に照明やセンサーノイズが変化する状況では、誤差や発散のリスクが増大します。さらに、各モデルには固有の限界があり、例えばUCMは接線方向の歪みを表現できず、Kannala-Brandtモデルは210◦を超える視野角では困難です。

対照的に、我々は異なるアプローチを採用し、カメラ逆投影を球面基底関数の線形結合として、つまり逆球面調和関数変換を介してモデル化します。このモデルでは、スカラー展開係数と球面領域境界を単純に推定します。

3. UniK3D

一般化可能な深度推定モデルや3Dシーン推定モデルは、多様なカメラ構成への適応においてしばしば大きな課題に直面します。既存の手法は、通常、ピンホールモデルや正距円筒モデルといったカメラ固有の厳格な仮定に依存しているか、平行化などの膨大な前処理手順を必要とします。これらの制約により、非標準的なカメラ投影形状を持つ現実世界のシナリオへの適用が制限されます。対照的に、私たちのモデルUniK3Dは、あらゆるシーンとあらゆるカメラ構成において単眼3D形状推定を可能にする新たなフレームワークを導入します。

まず、3.1節で3D出力空間の設計とカメラの内部表現について紹介します。この表現は、あらゆる逆投影問題に対応できるよう、意図的に可能な限り汎用的に定式化されています。予備研究を通して、一貫した問題が観察されました。それは、広い視野角を含む多様なカメラタイプで学習させた場合でも、ネットワークの予測値が狭い視野角に収縮してしまうことです。単純なデータ再調整戦略では、この現象に対処するには不十分であることが判明しました。この問題を解決するために、逆投影収縮を防ぐことを目的とした、一連のアーキテクチャと設計の介入策を開発しました。詳細は3.2節で説明します。3.3節では、モデルのアーキテクチャ、最適化戦略、そしてアプローチを支える具体的な設計関数と損失関数について説明します。図2に、この手法の概要を示します。

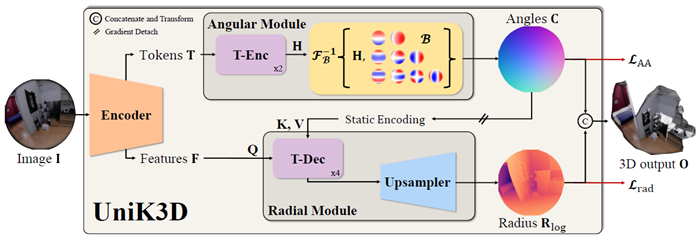
図2. モデルアーキテクチャ。UniK3Dは、単一の入力画像のみを利用して、任意のカメラの3D出力ポイントクラウド(\(\mathbf O\))を生成します。カメラの射影形状は角度モジュールによって予測されます。カメラ表現は、単位球面S3に逆投影された光線束の方位角と極角(\(\mathbf C\))に対応します。エンコーダーからのクラストークンは、2つのTransformer Encoder (TEnc)層によって処理され、定数成分のない3次までの球面調和関数の有限基底(\(\mathcal B\))によって定義される逆球面変換\(\mathcal F_{\mathcal B}^{−1}\{\mathbf H\}\)の15個の係数(\(\mathbf H\))を取得します。ラジアルモジュールの角度情報にはストップグラディエントが適用され、外部情報の流れをシミュレートします。「静的エンコーディング」とは、内部特徴の次元数と一致する正弦波エンコーディングを指します。ラジアルモジュールは、入力解像度ごとに1つずつ、Transformer Decoder (T-Dec) ブロックで構成され、ブートストラップされたカメラ表現に基づいてエンコーダーの特徴量を調整するために利用されます。この調整により、シーンスケールと射影幾何学に関する事前知識が注入されます。ラジアル出力 (\(\mathbf R_{log}\)) は、学習可能なアップサンプリングモジュールを介してカメラ認識特徴量を処理することで得られます。最終出力は、カメラテンソルとラジアルテンソルの連結 (\(\mathbf C||\mathbf R_{log}\)) です。直交座標3D出力を得るために閉形式座標変換が適用されますが、非対称角度損失\(\mathcal L_{AA}\)とラジアル座標を使用して、角度座標に直接監督が適用されます。

3.1. 表現

出力空間　UniK3Dの出力表現は、あらゆるシーンおよびカメラ構成と普遍的に互換性を持つように設計されており、各入力画像に対して直接的なメトリック3Dシーン推定を提供します。[60]で提示された分離戦略を参考に、我々のアプローチはカメラパラメータをシーンの形状から分離します。具体的には、カメラを稠密テンソル \(\mathbf C = θ||\phi\) を使用して表現します。ここで、\(θ\) は極角、\(\phi\) は方位角であり、標準的な球面座標と一致しています。ただし、従来の垂直深度ベースの表現に頼るのではなく、完全な球面フレームワーク内のシーン範囲成分としてユークリッド半径（カメラ中心からの距離）を使用します。この設計選択により、画像に投影された物体の寸法は半径に応じて一義的に変化することが保証されます。これは深度表現の特徴ではなく、深度表現の学習をはるかに困難にします。さらに、球面フレームワークは、XY平面付近の点を扱う際の数値的安定性を向上させます。この領域は、従来の手法では大きな勾配のために課題に直面することが一般的でした。本研究では、球面表現を全単射変換を用いて直交座標に変換し、シーンの3Dジオメトリを出力3D点群Oとして正確に捉えます。

カメラ内部空間　UniK3Dでは、様々なピクセルの視線方向を表す密な光線束は基底分解によって表現され、柔軟で包括的な角度表現を提供します。図2に示すように、角度モジュールは、エンコーダのクラストークン（\(\mathbf T\)と表記）から導出される係数テンソル\(\mathbf H\)を予測します。これらの係数は、定義済みの基底である球面調和関数（SH）基底に対応しています。\(\mathbf H\)から光線束を次のように再構成します。 \[ \mathbf C=\mathcal F_{\mathcal B}^{-1}\{\mathbf H\}=\sum_{l=0}^L\sum_{m=-l}^l \mathbf H_{lm}\mathcal B_{lm}(\theta,\phi) \tag{1} \] ここで、\(\mathbf C\) は再構成された角度場を表し、\(\mathcal F_{\mathcal B}^{−1}\) は SH 基底 \(\mathcal B\) を用いた係数空間から角度空間への逆変換を表します。\(\mathcal B_{lm}(θ, ϕ)\) は SH 基底関数、すなわちルジャンドル多項式であり、\(\mathbf H_{lm}\) は予測係数です。ここで、\(l\) と \(m\) はそれぞれ高調波の次数と次数を表します。この逆変換は、\(\mathbb R^n× \mathbb S^3\) から \(\mathbb S^3\) への内積として実装されます。SH 基底領域は、4 つのパラメーターによって定義されます。参照フレームの一般化された「主点」、すなわち極、および水平および垂直 FoV です。この定式化により、出力の連続性や微分可能性といった重要な特性を確保しながら、複雑な光線分布を簡潔かつ暗黙的に記述することが可能になります。

さらに、SH基底は高いスパース性を備えており、定数成分のない3次基底で15個の高調波と同数の係数のみで、ほとんどのカメラタイプの内部特性を正確に表現できます。このSHベースの表現を活用し、極とFoVパラメータによって領域を定義することで、UniK3Dはわずか19個のパラメータで、ほぼあらゆるカメラ形状に対応できる堅牢で柔軟なフレームワークを実現します。

3.2. 分布縮小の防止

非対称角度損失　ニューラルネットワークは、トレーニングデータ中で最も頻出するモードに回帰する傾向があり、分布の裾野を無視することがよくあります。私たちのケースでは、このバイアスにより、UniK3Dは出力において広視野角を過小評価することになります。これは、ほとんどの視覚データセットが狭視野角のピンホールカメラに大きく偏っているためです。これは、正確な広視野角予測を必要とするシナリオではパフォーマンスの低下につながります。この問題を克服するために、私たちは、ロバストな統計的推定量と決定理論の原則、すなわちタイプIエラーとタイプIIエラー[51]に着想を得た、分位回帰に基づく非対称角度損失を導入します。損失関数は次のように定義されます。 \[ \mathcal L_{AA}^\alpha (\hat{\theta},\theta^*)=\alpha\sum_{\hat{\theta}\gt \theta^*} \left|\hat{\theta}-\theta^*\right|+(1-\alpha)\sum_{\hat{\theta}\leq\theta^*}\left|\hat{\theta}-\theta^*\right| \tag{2} \] ここで、\(0 ≤ α ≤ 1\) は目標分位点、\(\hat{\theta}\) は予測角度、\(\theta^*\) は真の角度です。この定式化は、極角 \(θ\) の過大評価と過小評価の重み付けを調整します。\(α = 0.5\) の場合、損失は標準の平均絶対誤差 (MAE) に近づきますが、α を調整することで、過小評価された角度を強調し、回帰をより効果的にバランスさせることができます。単純なデータセットの再バランス調整 (3D シーンの多様性を変更し、特に複数のデータセット間で大幅な複雑さをもたらす可能性があります) とは異なり、私たちの損失は角度の不均衡に直接的かつ効率的に対処します。分位点回帰を用いることで、\(α\) の区間 [0, 1] における単純な探索へと複雑さを最小限に抑え、大規模かつ多様な学習シナリオに適した手法を実現します。この分位点に基づく戦略により、単純さと多様性を犠牲にすることなく角度分布のバイアスに対処することができ、堅牢でスケーラブルなソリューションを実現します。

カメラコンディショニングの強化　初期実験では、学習時とテスト時の両方で正解カメラレイを明示的に提供した場合でも、先行研究 [60] に倣ってモデルがカメラコンディショニングを効果的に利用するのに苦労していることがわかりました。この問題は、視野角の狭いピンホールカメラでは微妙でしたが、視野角の広い構成では顕著になりました。問題の根本は弱いコンディショニングにあります。つまり、モデルはカメラパラメータを幾何学的特徴から切り離すことができず、重要な視野角情報を統合することなく、局所的な異常をエンコーダ特徴空間に戻してしまうのです。その結果、テスト時に正確なカメラパラメータを与えられたとしても、モデルはこの情報を無視したり、誤った方向に進んだりする可能性があります。

これに対処するため、我々はカメラデータが訓練開始時から明確かつ明示的に構造化されている必要があると仮定する。この目的のため、UniK3Dではカメラレイの静的（学習不可能な）エンコーディングを実装し、カリキュラム学習戦略を採用して、正解カメラパラメータをラジアルモジュールに入力することから予測パラメータへと徐々に移行する。特に、正解カメラは確率\(1 − tanh(\frac{s}{10^5})\)でラジアルモジュールに入力される。ここで、\(s\)は現在の最適化ステップである。外部条件付けを強化するために、ラジアルモジュールに入力されるカメラ出力から勾配を切り離し、モデルがカメラの条件付けを損なう可能性のあるフィードバック機構に依存するのを防ぐ。さらに、条件付けのショートカットを回避するため、ラジアルモジュールのトランスフォーマーデコーダーのクロスアテンション層において、LayerScale [68]などの学習可能なゲインを無効化する。これらの戦略により、モデルはカメラ情報を効果的に活用してエンコーダー機能を調整し、3D予測の堅牢性を高めることができます。

3.3. ネットワーク設計

アーキテクチャ　図2に示すように、私たちのネットワークはエンコーダバックボーン、角度付きモジュール、および放射状モジュールで構成されています。エンコーダはViTベース[15]であり、密な特徴\(\mathbf F ∈ \mathbb R^{h×w×C×4}\)（ここで\((h,w) = ( \frac{H}{14} ,\frac{W}{14} )\)）とクラストークンTを抽出します。角度付きモジュールはこれらのクラストークンを処理し、3つのドメインパラメータと15の球面係数プロトタイプに分割された512チャネル表現に投影します。これらのトークンは、8つのヘッドを持つTransformer Encoder（T-Enc）の2つの層を通過し、スカラー値に投影されます。 3つのドメインパラメータの値は、主点（2）と水平視野（1）を定義し、高調波の間隔を決定します。我々は正方形ピクセルを仮定しているため、垂直視野用の追加の4番目のパラメータを学習するのではなく、この4番目のパラメータを水平視野から直接計算します。15個の球面係数は、3次SH基底を用いて、（1）に従って逆SH変換されます。角度モジュールからクラストークンに流れる勾配は0.1倍されます。これは、エンコーダの重みに対するカメラ誘起勾配の大きさが、放射状誘起勾配の約10倍であることが経験的に判明したためです。

ラジアルモジュールはまず、高密度エンコーダ特徴量Fを、解像度ごとに1つずつ、4つの並列層と1つのヘッドを持つTransformer Decoder (T-Dec)で処理します。これらの層は、正弦波符号化された角度表現に基づいてFを条件付けます。\(\mathbf C\) (付録A参照)。条件付けされた特徴量は512チャンネルテンソルに投影され、ラジアル特徴量\(\mathbf D ∈ \mathbb R^{h×w×512}\) を形成します。これらのラジアル特徴量はその後、残差畳み込みブロックと学習可能なアップサンプリング手法（双線形アップサンプリングに続いて1×1畳み込み）を用いて入力解像度にアップサンプリングされます。アップサンプリングされた特徴量からラジアル対数スケール出力 \(\mathbf R_{log} ∈ \mathbb R^{H×W}\) が計算され、要素ごとの累乗により \(\mathbf R\) に変換されます。最終的な3D球面出力 \(\mathbf O = \mathbf C||\mathbf R\) は、球面座標から直交座標への変換を用いて、直交座標点群 \(\mathbf O ∈ \mathbb R^{H×W×3}\) に変換されます。また、\(\mathbf R_{log}\) を計算するラジアルモジュールの最初のヘッドに加えて、アップサンプリングされたD特徴量を入力する第2の投影ヘッドを組み込むことで、ラジアル出力の信頼度マップ (Σ) を予測します。

最適化　最適化プロセスは3つの異なる損失によって定義されます。角度損失 \(\mathcal L_{AA}\) は \(θ\) と \(ϕ\) にそれぞれ \(\mathcal L_{AA}^{0.7}\) と \(\mathcal L_{AA}^0.5\) を適用します。最終的な角度損失は次のように表されます。 \[ \mathcal L_A(\hat{\mathbf C},\mathbf C^*)=\beta\mathcal L_{AA}^{0.7}(\hat{\theta},\theta^*)+(1-\beta)\mathcal L_{AA}^{0.5} (\hat{\phi},\phi^*) \tag{3} \] ここで、\((\hat{\cdot})\) と \((·)^∗\) はそれぞれ予測と正解の識別子として機能し、\(β = 0.75\) です。\(\mathcal L_{AA}^{0.5}\) は、主点に対する方位角次元 \(\phi\) が予測の縮小の影響を受けないため、標準の対称 L1 損失に対応することに注意してください。ここでのラジアル損失は、GT カメラによって取得された予測半径と GT 対数半径、および深度間の L1 損失です: \(\mathcal L_{rad} = \left|\left|\hat{\mathbf R}_{log}-\mathbf R_{log}^*\right|\right|_1\)。信頼度損失は、分離ラジアル損失と逆予測信頼度との間のL1損失、\(\Sigma: \mathcal L_{conf} = \left|\left| |\hat{\mathbf R}_{log}-\mathbf R_{log}^*|-\Sigma\right|\right|_1\)です。損失は3つの損失の線形結合です: \(\mathcal L_A + η\mathcal L_{rad} + γ\mathcal L_{conf}\)、ただし\(η = 2\)および\(γ = 0.1\)。

4. 実験

トレーニングデータセット　トレーニングデータセットは26種類のソースから構成されています。A2D2 [23]、aiMotive [48]、Argoverse2 [77]、 ARKit-Scenes [5]、ASE [17]、BEDLAM [8]、Blended-MVS [83]、DL3DV [44]、DrivingStereo [79]、DynamicReplica [31]、EDEN [37]、FutureHouse [42]、HOI4D [46]、 HM3D [62]、Matterport3D [11]、Mapillary-PSD [1]、 MatrixCity [40]、MegaDepth [41]、NianticMapFree [3]、 PointOdyssey [88]、ScanNet [12]、ScanNet++ (iPhone) [84]、 TartanAir [75] Taskonomy [87]、Waymo [67]、WildRGBD [78]。詳細は補足資料に記載されています。

ゼロショットテストデータセット　モデルの一般化可能性を評価するために、トレーニング中には使用されていない13のデータセットでモデルをテストしました。これらのデータセットは、カメラの種類に基づいて4つの異なるドメインに分類されています。1) 狭いFoV（S.FoV）、つまりFoV < 90◦、2) 放射状および接線方向の歪みがある狭いFoV（S.FoVDist）、3) 広いFoV（L.FoV）、つまりFoV > 120◦、4) 視野角が360◦のパノラマ（Pano）です。具体的には、S.FoVグループは、NYU-Depth V2 [50]、KITTI Eigen-split [21]、nuScenes [10]の検証分割、およびIBims-1 [34]、ETH-3D [65]、Diode Indoor [70]のフルデータセットに対応しています。S.FoVDistは、IBims-1、ETH-3D、Diode Indoorから人工的に歪ませた画像で構成されています（詳細は補足資料を参照）。L.FoVは、ADT [55]、ScanNet++ (DSLR) [84]、KITTI360 [43]をミックスしたものです。Panoramic (Pano)は、Stanford-2D3D [2]のフルデータセットに対応しています。

評価の詳細　すべての手法は、公平かつ一貫性のあるパイプラインを用いて再評価されました。特に、テスト時の拡張は利用せず、すべてのゼロショット評価に同じ重みセットを使用します。各手法のゼロショットモデルに対応するチェックポイントを使用します。つまり、KITTIまたはNYUで微調整されていません。主な実験で使用された指標は、\(δ_1^{SSI}, F_A\)、および\(ρ_A\)です。その他の指標は付録Cに報告されています。\(δ_1^{SSI}\)は、スケールおよびシフト不変の深度推定性能を測定します。\(F_A\)は、データセットの最大深度の1/20までのF1スコア[54]の曲線下面積(AUC)であり、単眼3D推定を評価します。 \(ρ_A\) はカメラの性能を評価し、S.FoV、L.Fov、Panoそれぞれについて、15◦、20◦、30◦までのカメラ光線の平均角度誤差のAUCです。焦点距離やFoVに基づくようなパラメトリック評価は、多様なカメラモデル間での一般性に欠けるため、使用を避けています。代わりに、選択した指標はあらゆるタイプのカメラへの適用性を確保し、評価の公平性と一貫性を維持します。表16と17は、標準的な方法に従って、最終チェックポイントをKITTIとNYU-Depth V2で学習し、ドメイン内評価を行うことで、UniK3Dの微調整能力を示しています。

実装の詳細　UniK3DはPyTorch [57]とCUDA [52]で実装されています。学習には、初期学習率5×10^{−5}でAdamW [47]最適化器（β_1 = 0.9、β_2 = 0.999）を使用します。学習率は、各実験のバックボーンの重みに対して10の係数で分割され、重みの減衰は0.1に設定されます。学習率スケジューラとしてコサインアニーリングを利用し、学習全体の30%から10分の1にします。最適化の反復回数は25万回で、バッチサイズは128です。学習時間は16台のNVIDIA 4090で6日間です。データセットのサンプリング手順は重み付きサンプラーに従います。各データセットの重みはシーン数です。我々の拡張は幾何学的および測光的であり、前者ではランダムなサイズ変更と切り取り、後者では明度、ガンマ、彩度、色相のシフトを行う。画像比率はバッチごとに2:1から9:16の間でランダムにサンプリングする。ViT [15] バックボーンは、DINO事前学習済み [53] モデルの重みで初期化される。アブレーションについては、ViT-S バックボーンを用いて10万ステップの学習を実行し、学習パイプラインはメインの実験と同じである。

4.1. 最先端技術との比較

表1は、様々なFoVと画像タイプにおけるUniK3Dと既存のSotA手法の包括的な比較を示しています。本モデルは、特に困難な広FoVおよびパノラマシナリオにおいて、一貫して従来モデルを上回る性能を発揮します。例えば、L.FoV領域では、UniK3Dは\(δ_1^{SSI}\)で91.2%、\(F_A\)で71.6%という驚異的な性能を達成し、次点の手法をそれぞれ20%以上、40%以上上回ります。この大幅な改善は、広いFoVを扱う際の統合球面フレームワークの堅牢性を強調しています。パノカテゴリーでは、モデルの\(δ_1^{SSI}\)スコアと\(F_A\)スコアがそれぞれ71.2%と66.1%となり、新たなSotAを樹立しました。これは、極端なカメラ設定下でも3Dジオメトリを効果的に再構築できることを示しています。これらの結果は、SHベースのカメラモデルやラジアル出力表現といった設計上の選択が、複雑で多様なカメラ設定において高い性能を維持するために不可欠であることを実証しています。

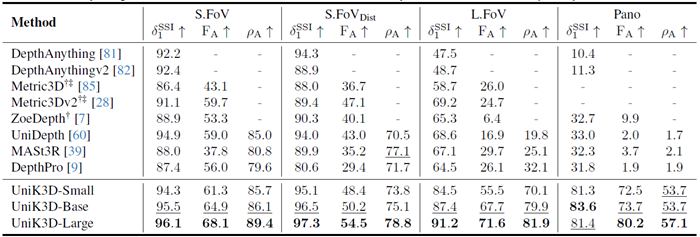
表1. 多様なカメラドメインにおけるゼロショット評価の比較。検証セット：S.FoVにはNYU、KITTI、IBims-1、ETH-3D、nuScenes、Diode Indoorが含まれます。S.FoVDistにはIBims-1、ETH-3D、合成歪みを適用したDiode Indoorが含まれます。L.FoVにはADT、ScanNet++ (DSLR)、KITTI360が含まれます。PanoにはStanford-2D3Dが含まれます。すべてのモデルはViT-Lバックボーンを使用しています。欠損値（-）は、モデルがそれぞれの出力を生成できないことを示します。Metric3DおよびMetric3Dv2は焦点距離が未定義であるため、パノラマ画像では評価できません。†：3D再構成には正解（GT）カメラが必要です。‡：2D深度マップ推論にはGTカメラが必要です。

さらに、図3は、UniK3Dが様々な歪んだカメラから得られたシーンの3D形状を推定できることを明確に示しています。これは、2列目、3列目、4列目に示されているように、非従来型またはピンホールカメラ以外のカメラ画像では失敗する他の手法とは対照的です。Metric3D、Metric3Dv2、ZoeDepthは \(F_A\) スコアに正解カメラパラメータを使用して評価されるのに対し、UniK3D、UniDepth、MASt3R、DepthProは予測されたカメラに依存していることを強調しておくことが重要です。この追加の難しさにもかかわらず、UniK3Dは優れた3D再構築性能を示し、正確なカメラ情報が得られない現実世界の状況に対応できる強みを示しています。興味深いことに、私たちの手法は、より従来型の小さなFoVシナリオでも性能を犠牲にしません。 UniK3Dは、S.FoV設定において\(δ_1^{SSI}\)が94.3となり、トップランクを維持し、これまでの主要手法を上回りました。このバランスは、L.FoV表現における我々の進歩が、S.FoVタスクにおけるモデルの有効性を損なわないことを示しています。\(F_A\) スコアはS.FoVにおいて高い水準を維持しており、\(ρ_A\) 指標は、我々のモデルが一貫して正確なカメラパラメータ推定を提供していることを示しています。

図 3. 定性的な比較。連続する行の各ペアは 1 つのテストサンプルを表します。奇数行には入力 RGB 画像と 2D エラーマップが表示され、絶対相対誤差に基づいてクールウォームカラーマップで色分けされています (パノラマ画像の場合、誤差は深度ではなく距離に基づいて計算されます)。公平な比較を確実にするために、すべてのモデルについて、GT ベースのシフトおよびスケーリングされた出力で誤差が計算されます。偶数行には 3D ポイントクラウドの正解と予測が表示されます。最後の列には、絶対相対誤差の特定のカラーマップ範囲が表示されます。各行ペアの主な観察結果: (1) 競合手法は正の深度のみに制限されており、視野が大きい場合、シーンが大きく歪みます。(2) 表現可能だが大きい視野 (180 ◦) の場合、UniK3D 出力だけが顕著な視野収縮の影響を受けません。(3) 中程度の視野 (FoV) を持つ画像ですが、境界の歪みが強い場合 (例:魚眼レンズとは異なり、UniK3Dは平面性とシーン全体の構造を維持できます。(4) 私たちのアプローチは、標準的なピンホール画像に対しても正確な3D推定値を提供します。

さらに、表2に示すように、UniK3Dは正距円筒画像に特化した手法と競合します。これは、当社のモデルが、特定の領域のパフォーマンスを損なうことなく、トレーニング時にさまざまなシーンやカメラ領域を組み込むことができることを示しています。

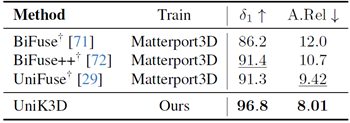
表2. ゼロショット法と正距円筒画像に特化した手法の比較。全ての手法はStanford-2D3D [2] を用いてゼロショットテストされている。競合手法は全て正距円筒画像を用いて学習されている。我々の学習セットには、2%サンプリングのMatterport3D [11] が含まれている。

4.2. アブレーション研究

データ　表3は、大きなFoVとカメラの歪みがあるデータセットとないデータセットにおける学習の効果を示しています。強いカメラの歪みのある画像を組み込むと、一般的にすべての領域でパフォーマンスが向上しますが、特に歪みのあるS.FoVやL.FoVなどの難しいケースでは顕著です。これは、より優れた汎化を実現するために、学習セットに多様なカメラジオメトリを含めることが重要であることを強調しています。ただし、対数深度表現を使用してパノラマ画像を表現することが難しいため、Panoの改善には限界があります。

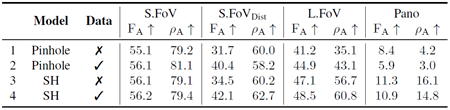
表3. データのアブレーション。データは、トレーニング画像に、実データまたはピンホールカメラから合成された、強く歪んだカメラ画像が含まれているかどうかを示します。出力表現：深度。

カメラモデル　表4に示すように、カメラ光線の基底としてSHを用いると、特にL.FoVとPanoにおいて、全体的に最も優れた性能が得られる。これは、多様なカメラモデルを捉える上で、我々の基底関数選択の有効性を強調している。対照的に、ノンパラメトリックモデルは \(F_A\) と \(ρ_A\) において性能が劣る。後者の定式化は純粋にデータ駆動型であるため、適切に一般化するにはかなり多くのデータが必要であると推測される。データ分布の裾野、すなわちL.FoVとPanoを過小評価する傾向がある一方で、より一般的な領域、すなわち歪みの有無にかかわらずS.FoVでは適切な性能を示す。レンズ収差のモデル化に典型的に用いられるゼルニケ多項式基底[18]は、その固有の平面構造のために、球面または正距円筒カメラ形状を表現するのが困難である。

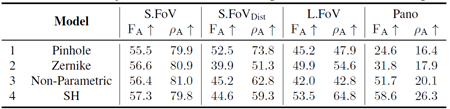
表4. カメラモデルにおけるアブレーション。モデルは、出力光線と内部調整に関するカメラモデルの種類に対応しています。ピンホール、ゼルニケ多項式係数、SH係数、またはノンパラメトリック（ピクセルあたり1光線を予測）です。すべての実験は、フルデータ、拡張、モデルコンポーネント、および放射状出力を用いて実施されています。

出力空間　表5は、予測空間の3次元目の異なる出力表現（直交座標Z軸（1行目と3行目）または球面半径（2行目と4行目））を比較したものです。結果から、半径表現を使用すると、パノおよびL.FoV設定での再構成メトリクスが向上することがわかります。これは、180度付近または180度を超えるFoVを扱う場合、深度はあまり効果的ではないためです。この改善は、放射状コンポーネントを、広範囲の形状を表現できるカメラモデル（例えば、SHベースのモデル（4行目と2行目））と組み合わせた場合にのみ実現されます。しかし、半径ベースの出力空間では、歪みのあるS.FoVの再構成精度が低下します（3行目と4行目）。この劣化は、半径表現が小さな角度の変化に敏感であり、小さくても歪みの大きいビューの精度に不釣り合いな影響を与えるために発生します。

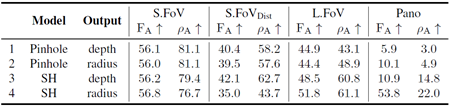
表5. 出力表現におけるアブレーション。出力とは、予測出力空間の3次元の種類を指します。直交座標Z軸の深度または球面半径（つまり距離）のいずれかです。すべての実験は、フルデータと拡張を用いて実施されています。

コンポーネント　表6は、非対称角度損失（\(\mathcal L_{AA}\)）と、カメラコンディショニングを強化するために設計された戦略の影響を検証しています。非対称損失と改善されたコンディショニングの両方を活用した完全なモデル（行3）は、特に歪んだ領域とL.FoV領域において、それらを活用しないモデルよりも大幅に優れた性能を発揮します。これは、逆投影における収縮を防ぎ、角度予測精度を向上させるという、組み合わせた戦略の有効性を示しています。全体的な向上は、むしろこれらの貢献を組み合わせることによる相乗効果によるものです。さらに、これらの戦略は、集約的な定量的結果では容易に表現できない可能性のある極端なケースを軽減することを目的としており、図4のように定性的なサンプルでは明確に確認できます。

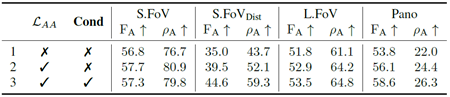
表6. ネットワーク構成要素のアブレーション。\(\mathcal L_{AA}\) は、非対称角度損失が使用されているかどうかを示し、そうでない場合はL1損失を示します。Cond は、セクション3.2で示した強化されたカメラコンディショニングの設計が使用されているかどうかを示します。すべての実験は、完全なデータと拡張、ラジアル出力表現、およびSHベースのカメラモデルを使用して実施されています。

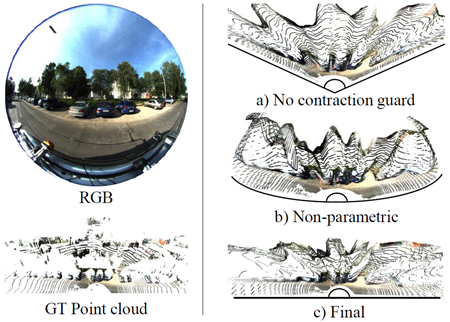
図4. FoVの影響。左の画像は、GT点群と並んで180◦のFoV全体を表現するという課題を示しています。FoVの縮小効果は、a)に示すように、「ガード」、すなわち非対称損失（\(\mathcal L_{AA}\)）とカメラコンディショニングが全く適用されていない場合に発生します。b)に示すように、事前分布が全く存在しない場合、逆投影が不可能で一貫性のない結果になる可能性があります。c)は最終的なUniK3Dを示しており、適切なカメラ逆投影モデルを用いることで広いFoVを復元できることを明確に示しています。

5. 結論

我々は、ピンホールから魚眼レンズ、パノラマまで、多様なカメラモデルにシームレスに汎用化する、単眼3D推定のための初のユニバーサルフレームワークであるUniK3Dを発表しました。我々のアプローチは、視野角の縮小を防ぐ戦略を導入し、あらゆる汎用カメラモデルへのバックプロジェクションのための柔軟で堅牢な設計を通じて、正確なメトリック3D推定をサポートします。トレーニングデータの多様性とカバレッジを拡大することで、UniK3Dの堅牢性と適用性はさらに向上する可能性がありますが、UniK3Dは既に、わずかな量のデータで、従来の最先端技術の能力をはるかに超える、未知のカメラや3Dシーン領域への強力な汎用化を実現しています。

謝辞

この研究は、トヨタ自動車ヨーロッパの研究プロジェクトTRACE-Z¨urichを通じて資金提供を受けています。

参考文献

[1] Manuel Lopez Antequera, Pau Gargallo, Markus Hofinger, Samuel Rota Bul`o, Yubin Kuang, and Peter Kontschieder. Mapillary planet-scale depth dataset. In The European Conference on Computer Vision (ECCV), pages 589–604. Springer International Publishing, 2020. 6, 15

[2] Iro Armeni, Sasha Sax, Amir R Zamir, and Silvio Savarese. Joint 2d-3d-semantic data for indoor scene understanding. arXiv preprint arXiv:1702.01105, 2017. 6, 7, 15

[3] Eduardo Arnold, Jamie Wynn, Sara Vicente, Guillermo Garcia-Hernando, A´ ron Monszpart, Victor Adrian Prisacariu, Daniyar Turmukhambetov, and Eric Brachmann. Map-free visual relocalization: Metric pose relative to a single image. In European Conference on Computer Vision (ECCV), 2022. 6, 15

[4] Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffrey E Hinton. Layer normalization. arXiv preprint arXiv:1607.06450, 2016. 13

[5] Gilad Baruch, Zhuoyuan Chen, Afshin Dehghan, Tal Dimry, Yuri Feigin, Peter Fu, Thomas Gebauer, Brandon Joffe, Daniel Kurz, Arik Schwartz, and Elad Shulman. ARKitscenes - a diverse real-world dataset for 3d indoor scene understanding using mobile RGB-d data. In Advances in Neural Information Processing Systems (NIPS), 2021. 6, 15

[6] Shariq Farooq Bhat, Ibraheem Alhashim, and Peter Wonka. Adabins: Depth estimation using adaptive bins. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 4008–4017, 2020. 2, 16

[7] Shariq Farooq Bhat, Reiner Birkl, Diana Wofk, Peter Wonka, and Matthias M¨uller. Zoedepth: Zero-shot transfer by combining relative and metric depth. arXiv preprint arXiv:2302.12288, 2023. 2, 6, 14, 16, 17, 18, 19

[8] Michael J. Black, Priyanka Patel, Joachim Tesch, and Jinlong Yang. BEDLAM: A synthetic dataset of bodies exhibiting detailed lifelike animated motion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 8726–8737, 2023. 6, 15

[9] Aleksei Bochkovskii, Ama¨el Delaunoy, Hugo Germain, Marcel Santos, Yichao Zhou, Stephan R Richter, and Vladlen Koltun. Depth pro: Sharp monocular metric depth in less than a second. arXiv preprint arXiv:2410.02073, 2024. 1, 2, 6, 14, 17, 18, 19

[10] Holger Caesar, Varun Bankiti, Alex H. Lang, Sourabh Vora, Venice Erin Liong, Qiang Xu, Anush Krishnan, Yu Pan, Giancarlo Baldan, and Oscar Beijbom. nuscenes: A multimodal dataset for autonomous driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020. 6, 15

[11] Angel Chang, Angela Dai, Thomas Funkhouser, Maciej Halber, Matthias Niessner, Manolis Savva, Shuran Song, Andy Zeng, and Yinda Zhang. Matterport3d: Learning from rgb-d data in indoor environments. In Proceedings of the International Conference on 3D Vision (3DV), 2017. 6, 15

[12] Angela Dai, Angel X. Chang, Manolis Savva, Maciej Halber, Thomas Funkhouser, and Matthias Nießner. Scannet: Richlyannotated 3d reconstructions of indoor scenes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2017. 6, 15

[13] Kangle Deng, Andrew Liu, Jun-Yan Zhu, and Deva Ramanan. Depth-supervised nerf: Fewer views and faster training for free. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 12882–12891, 2022. 1

[14] Xingshuai Dong, Matthew A Garratt, Sreenatha G Anavatti, and Hussein A Abbass. Towards real-time monocular depth estimation for robotics: A survey. IEEE Transactions on Intelligent Transportation Systems, 23(10):16940–16961, 2022. 1

[15] Alexey Dosovitskiy, Lucas Beyer, Alexander Kolesnikov, Dirk Weissenborn, Xiaohua Zhai, Thomas Unterthiner, Mostafa Dehghani, Matthias Minderer, Georg Heigold, Sylvain Gelly, Jakob Uszkoreit, and Neil Houlsby. An image is worth 16x16 words: Transformers for image recognition at scale. In International Conference on Learning Representations (ICLR). OpenReview.net, 2021. 5, 7, 13

[16] David Eigen, Christian Puhrsch, and Rob Fergus. Depth map prediction from a single image using a multi-scale deep network. In Advances in Neural Information Processing Systems (NeurIPS), pages 2366–2374. Neural information processing systems foundation, 2014. 2

[17] Jakob Engel, Kiran Somasundaram, Michael Goesele, Albert Sun, Alexander Gamino, Andrew Turner, Arjang Talattof, Arnie Yuan, Bilal Souti, Brighid Meredith, et al. Project aria: A new tool for egocentric multi-modal ai research. arXiv preprint arXiv:2308.13561, 2023. 6, 15

[18] Zernike Frits. Beugungstheorie des schneidenver-fahrens und seiner verbesserten form, der phasenkontrastmethode. Physica: Nonlinear Phenomena, 1:689–704, 1934. 8

[19] Huan Fu, Mingming Gong, Chaohui Wang, Kayhan Batmanghelich, and Dacheng Tao. Deep ordinal regression network for monocular depth estimation. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 2002–2011, 2018. 2

[20] Ravi Garg, B. G. Vijay Kumar, Gustavo Carneiro, and Ian Reid. Unsupervised cnn for single view depth estimation: Geometry to the rescue. Lecture Notes in Computer Science, 9912 LNCS:740–756, 2016. 17

[21] Andreas Geiger, Philip Lenz, and Raquel Urtasun. Are we ready for autonomous driving? The KITTI vision benchmark suite. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2012. 6, 15

[22] Christopher Geyer and Kostas Daniilidis. A unifying theory for central panoramic systems and practical applications. In The European Conference on Computer Vision (ECCV), 2000. 3

[23] Jakob Geyer, Yohannes Kassahun, Mentar Mahmudi, Xavier Ricou, Rupesh Durgesh, Andrew S. Chung, Lorenz Hauswald, Viet Hoang Pham, Maximilian M¨uhlegg, Sebastian Dorn, Tiffany Fernandez, Martin J¨anicke, Sudesh Mirashi, Chiragkumar Savani, Martin Sturm, Oleksandr Vorobiov, Martin Oelker, Sebastian Garreis, and Peter Schuberth. A2D2: Audi Autonomous Driving Dataset. arXiv preprint arXiv:2004.06320, 2020. 6, 15

[24] Vitor Guizilini, Igor Vasiljevic, Dian Chen, Rares, Ambrus, , and Adrien Gaidon. Towards zero-shot scale-aware monocular depth estimation. In Proceedings of the IEEE/CVF In-ternational Conference on Computer Vision (ICCV), pages 9233–9243, 2023. 1, 2

[25] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2016-December:770–778, 2015. 13

[26] Dan Hendrycks and Kevin Gimpel. Bridging nonlinearities and stochastic regularizers with gaussian error linear units. CoRR, abs/1606.08415, 2016. 13

[27] Noriaki Hirose and Kosuke Tahara. Depth360: Selfsupervised learning for monocular depth estimation using learnable camera distortion model. 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pages 317–324, 2021. 20

[28] Mu Hu, Wei Yin, Chi Zhang, Zhipeng Cai, Xiaoxiao Long, Hao Chen, Kaixuan Wang, Gang Yu, Chunhua Shen, and Shaojie Shen. Metric3d v2: A versatile monocular geometric foundation model for zero-shot metric depth and surface normal estimation. arXiv preprint arXiv:2404.15506, 2024. 2, 6, 14, 16, 17, 18, 19, 21

[29] Hualie Jiang, Zhe Sheng, Siyu Zhu, Zilong Dong, and Rui Huang. Unifuse: Unidirectional fusion for 360 panorama depth estimation. IEEE Robotics and Automation Letters (RAL), 6(2):1519–1526, 2021. 6

[30] Juho Kannala and Sami Sebastian Brandt. A generic camera model and calibration method for conventional, wide-angle, and fish-eye lenses. IEEE Transactions on Pattern Analysis and Machine Intelligence (T-PAMI, 28:1335–1340, 2006. 3, 15

[31] Nikita Karaev, Ignacio Rocco, Benjamin Graham, Natalia Neverova, Andrea Vedaldi, and Christian Rupprecht. Dynamicstereo: Consistent dynamic depth from stereo videos. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2023. 6, 15

[32] Bingxin Ke, Anton Obukhov, Shengyu Huang, Nando Metzger, Rodrigo Caye Daudt, and Konrad Schindler. Repurposing diffusion-based image generators for monocular depth estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 9492–9502, 2024. 1, 2

[33] Bogdan Khomutenko, Ga¨etan Garcia, and Philippe Martinet. An enhanced unified camera model. IEEE Robotics and Automation Letters (RA-L), 1:137–144, 2016. 3, 19

[34] Tobias Koch, Lukas Liebel, Marco K¨orner, and Friedrich Fraundorfer. Comparison of monocular depth estimation methods using geometrically relevant metrics on the IBims-1 dataset. Computer Vision and Image Understanding (CVIU), 191:102877, 2020. 6, 15, 16

[35] Varun Ravi Kumar, Senthil Kumar Yogamani, Markus Bach, Christian Witt, Stefan Milz, and Patrick M¨ader. Unrectdepthnet: Self-supervised monocular depth estimation using a generic framework for handling common camera distortion models. 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pages 8177–8183, 2020. 20

[36] Iro Laina, Christian Rupprecht, Vasileios Belagiannis, Federico Tombari, and Nassir Navab. Deeper depth prediction with fully convolutional residual networks. Proceedings of the International Conference on 3D Vision (3DV), pages 239– 248, 2016. 2

[37] Hoang-An Le, Thomas Mensink, Partha Das, Sezer Karaoglu, and Theo Gevers. Eden: Multimodal synthetic dataset of enclosed garden scenes. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), pages 1579–1589, 2021. 6, 15

[38] Jin Han Lee, Myung-Kyu Han, Dong Wook Ko, and Il Hong Suh. From big to small: Multi-scale local planar guidance for monocular depth estimation. CoRR, abs/1907.10326, 2019. 16

[39] Vincent Leroy, Yohann Cabon, and J´erˆome Revaud. Grounding image matching in 3d with mast3r. arXiv preprint arXiv:2406.09756, 2024. 5, 6, 17, 18, 19, 21

[40] Yixuan Li, Lihan Jiang, Linning Xu, Yuanbo Xiangli, Zhenzhi Wang, Dahua Lin, and Bo Dai. Matrixcity: A large-scale city dataset for city-scale neural rendering and beyond. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), pages 3205–3215, 2023. 6, 15

[41] Zhengqi Li and Noah Snavely. Megadepth: Learning singleview depth prediction from internet photos. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 2041–2050, 2018. 6, 15

[42] Zhen Li, Lingli Wang, Xiang Huang, Cihui Pan, and Jiaqi. Yang. Phyir: Physics-based inverse rendering for panoramic indoor images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022. 6, 15

[43] Yiyi Liao, Jun Xie, and Andreas Geiger. KITTI-360: A novel dataset and benchmarks for urban scene understanding in 2d and 3d. IEEE Transactions on Pattern Analysis and Machine Intelligence (T-PAMI), 2022. 7, 15

[44] Lu Ling, Yichen Sheng, Zhi Tu, Wentian Zhao, Cheng Xin, KunWan, Lantao Yu, Qianyu Guo, Zixun Yu, Yawen Lu, et al. DL3DV-10k: A large-scale scene dataset for deep learningbased 3d vision. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 22160–22169, 2024. 6, 15

[45] Fayao Liu, Chunhua Shen, Guosheng Lin, and Ian Reid. Learning depth from single monocular images using deep convolutional neural fields. IEEE Transactions on Pattern Analysis and Machine Intelligence (T-PAMI), 38:2024–2039, 2015. 2

[46] Yunze Liu, Yun Liu, Che Jiang, Kangbo Lyu, Weikang Wan, Hao Shen, Boqiang Liang, Zhoujie Fu, He Wang, and Li Yi. Hoi4d: A 4d egocentric dataset for category-level humanobject interaction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 21013–21022, 2022. 6, 15

[47] Ilya Loshchilov and Frank Hutter. Decoupled weight decay regularization. 7th International Conference on Learning Representations, ICLR 2019, 2017. 7, 15

[48] Tamas Matuszka, Ivan Barton, A´ da´m Butykai, Pe´ter Hajas, D´avid Kiss, Domonkos Kov´acs, S´andor Kuns´agi-M´at´e, P´eter Lengyel, G´abor N´emeth, Levente Pet˝o, Dezs˝o Ribli, D´avid Szeghy, Szabolcs Vajna, and Balint Viktor Varga. aimotive dataset: A multimodal dataset for robust autonomous driving with long-range perception. In International Conference on Learning Representations (ICLR) Workshop on Scene Representations for Autonomous Driving, 2023. 6, 15

[49] Christopher Mei and Patrick Rives. Single view point omnidirectional camera calibration from planar grids. Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), pages 3945–3950, 2007. 3, 15

[50] Pushmeet Kohli Nathan Silberman, Derek Hoiem and Rob Fergus. Indoor segmentation and support inference from rgbd images. In The European Conference on Computer Vision (ECCV), 2012. 6, 15

[51] Jerzy Neyman and Egon Sharpe Pearson. On the problem of the most efficient tests of statistical hypotheses. Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character, 231(694-706):289–337, 1933. 4

[52] John Nickolls, Ian Buck, Michael Garland, and Kevin Skadron. Scalable parallel programming with cuda: Is cuda the parallel programming model that application developers have been waiting for? Queue, 6(2):40–53, 2008. 7

[53] Maxime Oquab, Timoth´ee Darcet, Th´eo Moutakanni, Huy Vo, Marc Szafraniec, Vasil Khalidov, Pierre Fernandez, Daniel Haziza, Francisco Massa, Alaaeldin El-Nouby, et al. Dinov2: Learning robust visual features without supervision. arXiv preprint arXiv:2304.07193, 2023. 7

[54] Evin Pınar O¨ rnek, Shristi Mudgal, Johanna Wald, Yida Wang, Nassir Navab, and Federico Tombari. From 2d to 3d: Rethinking benchmarking of monocular depth prediction. arXiv preprint arXiv:2203.08122, 2022. 7

[55] Xiaqing Pan, Nicholas Charron, Yongqian Yang, Scott Peters, Thomas Whelan, Chen Kong, Omkar Parkhi, Richard Newcombe, and Yuheng Carl Ren. Aria digital twin: A new benchmark dataset for egocentric 3d machine perception. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), pages 20133–20143, 2023. 7, 15

[56] Dennis Park, Rares Ambrus, Vitor Guizilini, Jie Li, and Adrien Gaidon. Is pseudo-lidar needed for monocular 3d object detection? In IEEE/CVF International Conference on Computer Vision (ICCV), 2021. 1

[57] Adam Paszke, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, Alban Desmaison, Andreas Kopf, Edward Yang, Zachary DeVito, Martin Raison, Alykhan Tejani, Sasank Chilamkurthy, Benoit Steiner, Lu Fang, Junjie Bai, and Soumith Chintala. Pytorch: An imperative style, high-performance deep learning library. In Advances in Neural Information Processing Systems (NeurIPS), pages 8024–8035. Curran Associates, Inc., 2019. 7

[58] Vaishakh Patil, Christos Sakaridis, Alexander Liniger, and Luc Van Gool. P3Depth: Monocular depth estimation with a piecewise planarity prior. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022. 2

[59] Luigi Piccinelli, Christos Sakaridis, and Fisher Yu. iDisc: Internal discretization for monocular depth estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2023. 2, 16

[60] Luigi Piccinelli, Yung-Hsu Yang, Christos Sakaridis, Mattia Segu, Siyuan Li, Luc Van Gool, and Fisher Yu. Unidepth Universal monocular metric depth estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 10106–10116, 2024. 1, 2, 3, 4, 5, 6, 14, 17, 18, 19, 20, 21

[61] Luigi Piccinelli, Christos Sakaridis, Yung-Hsu Yang, Mattia Segu, Siyuan Li, Wim Abbeloos, and Luc Van Gool. UniDepthV2: Universal monocular metric depth estimation made simpler. arXiv:2502.20110, 2025. 1, 2

[62] Santhosh Kumar Ramakrishnan, Aaron Gokaslan, Erik Wijmans, Oleksandr Maksymets, Alexander Clegg, John M Turner, Eric Undersander, Wojciech Galuba, Andrew Westbury, Angel X Chang, Manolis Savva, Yili Zhao, and Dhruv Batra. Habitat-matterport 3d dataset (HM3d): 1000 largescale 3d environments for embodied AI. In Advances in Neural Information Processing Systems (NIPS), 2021. 6, 15

[63] Ren´e Ranftl, Katrin Lasinger, David Hafner, Konrad Schindler, and Vladlen Koltun. Towards robust monocular depth estimation: Mixing datasets for zero-shot cross-dataset transfer. IEEE Transactions on Pattern Analysis and Machine Intelligence (T-PAMI), 44(3):1623–1637, 2020. 1, 2

[64] Davide Scaramuzza. Omnidirectional camera. In Computer Vision, A Reference Guide, 2014. 3

[65] Thomas Sch¨ops, Johannes L. Sch¨onberger, Silvano Galliani, Torsten Sattler, Konrad Schindler, Marc Pollefeys, and Andreas Geiger. A multi-view stereo benchmark with highresolution images and multi-camera videos. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2017. 6, 15, 16

[66] Niklaus Simon and Feng Liu. Softmax splatting for video frame interpolation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020. 16

[67] Pei Sun, Henrik Kretzschmar, Xerxes Dotiwalla, Aurelien Chouard, Vijaysai Patnaik, Paul Tsui, James Guo, Yin Zhou, Yuning Chai, Benjamin Caine, et al. Scalability in perception for autonomous driving: Waymo open dataset. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 2446–2454, 2020. 6, 15

[68] Hugo Touvron, Matthieu Cord, Alexandre Sablayrolles, Gabriel Synnaeve, and Herv´e J´egou. Going deeper with image transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), pages 32–42, 2021. 5

[69] Vladyslav C. Usenko, Nikolaus Demmel, and Daniel Cremers. The double sphere camera model. International Conference on 3D Vision (3DV), pages 552–560, 2018. 3, 19

[70] Igor Vasiljevic, Nicholas I. Kolkin, Shanyi Zhang, Ruotian Luo, Haochen Wang, Falcon Z. Dai, Andrea F. Daniele, Mohammadreza Mostajabi, Steven Basart, Matthew R. Walter, and Gregory Shakhnarovich. DIODE: A dense indoor and outdoor depth dataset. CoRR, abs/1908.00463, 2019. 7, 15, 16

[71] Fu-En Wang, Yu-Hsuan Yeh, Min Sun, Wei-Chen Chiu, and Yi-Hsuan Tsai. Bifuse: Monocular 360 depth estimation via bi-projection fusion. In The IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020. 6

[72] Fu-En Wang, Yu-Hsuan Yeh, Yi-Hsuan Tsai, Wei-Chen Chiu, and Min Sun. Bifuse++: Self-supervised and efficient biprojection fusion for 360 depth estimation. IEEE Transactions on Pattern Analysis and Machine Intelligence (T-PAMI), 45 (5):5448–5460, 2022. 6

[73] Ruicheng Wang, Sicheng Xu, Cassie Dai, Jianfeng Xiang, Yu Deng, Xin Tong, and Jiaolong Yang. Moge: Unlocking accurate monocular geometry estimation for open-domain images with optimal training supervision. arXiv preprint arXiv:2410.19115, 2024. 2

[74] Shuzhe Wang, Vincent Leroy, Yohann Cabon, Boris Chidlovskii, and J´erˆome Revaud. Dust3r: Geometric 3d vision made easy. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 20697–20709, 2024. 19

[75] Wenshan Wang, Delong Zhu, Xiangwei Wang, Yaoyu Hu, Yuheng Qiu, Chen Wang, Yafei Hu, Ashish Kapoor, and Sebastian Scherer. Tartanair: A dataset to push the limits of visual slam. In 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pages 4909–4916. IEEE, 2020. 6, 15

[76] Yan Wang, Wei-Lun Chao, Divyansh Garg, Bharath Hariharan, Mark Campbell, and Kilian Q Weinberger. Pseudolidar from visual depth estimation: Bridging the gap in 3d object detection for autonomous driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 8445–8453, 2019. 1

[77] Benjamin Wilson, William Qi, Tanmay Agarwal, John Lambert, Jagjeet Singh, Siddhesh Khandelwal, Bowen Pan, Ratnesh Kumar, Andrew Hartnett, Jhony Kaesemodel Pontes, Deva Ramanan, Peter Carr, and James Hays. Argoverse 2: Next generation datasets for self-driving perception and forecasting. In Advances in Neural Information Processing Systems, 2021. 6, 15

[78] Hongchi Xia, Yang Fu, Sifei Liu, and Xiaolong Wang. Rgbd objects in the wild: Scaling real-world 3d object learning from rgb-d videos. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 22378–22389, 2024. 6, 15

[79] Guorun Yang, Xiao Song, Chaoqin Huang, Zhidong Deng, Jianping Shi, and Bolei Zhou. Drivingstereo: A large-scale dataset for stereo matching in autonomous driving scenarios. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2019. 6, 15

[80] Guanglei Yang, Hao Tang, Mingli Ding, Nicu Sebe, and Elisa Ricci. Transformer-based attention networks for continuous pixel-wise prediction. Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), pages 16249– 16259, 2021. 2

[81] Lihe Yang, Bingyi Kang, Zilong Huang, Xiaogang Xu, Jiashi Feng, and Hengshuang Zhao. Depth anything: Unleashing the power of large-scale unlabeled data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 10371–10381, 2024. 1, 2, 5, 6, 17, 18, 19

[82] Lihe Yang, Bingyi Kang, Zilong Huang, Zhen Zhao, Xiaogang Xu, Jiashi Feng, and Hengshuang Zhao. Depth anything v2. arXiv preprint arXiv:2406.09414, 2024. 2, 6, 14, 16, 17, 18, 19

[83] Yao Yao, Zixin Luo, Shiwei Li, Jingyang Zhang, Yufan Ren, Lei Zhou, Tian Fang, and Long Quan. Blendedmvs: A large largescale dataset for generalized multi-view stereo networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 1790–1799, 2020. 6, 15

[84] Chandan Yeshwanth, Yueh-Cheng Liu, Matthias Nießner, and Angela Dai. Scannet++: A high-fidelity dataset of 3d indoor scenes. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2023. 6, 7, 15

[85] Wei Yin, Chi Zhang, Hao Chen, Zhipeng Cai, Gang Yu, Kaixuan Wang, Xiaozhi Chen, and Chunhua Shen. Metric3d: Towards zero-shot metric 3d prediction from a single image. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), pages 9043–9053, 2023. 1, 2, 6, 16, 17, 18, 19

[86] Weihao Yuan, Xiaodong Gu, Zuozhuo Dai, Siyu Zhu, and Ping Tan. Neural window fully-connected crfs for monocular depth estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 3906–3915. IEEE, 2022. 2, 16

[87] Amir R Zamir, Alexander Sax, William B Shen, Leonidas Guibas, Jitendra Malik, and Silvio Savarese. Taskonomy: Disentangling task transfer learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). IEEE, 2018. 6, 15

[88] Yang Zheng, Adam W Harley, Bokui Shen, Gordon Wetzstein, and Leonidas J Guibas. Pointodyssey: A large-scale synthetic dataset for long-term point tracking. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), pages 19855–19865, 2023. 6, 15

[89] Brady Zhou, Philipp Kr¨ahenb¨uhl, and Vladlen Koltun. Does computer vision matter for action? Science Robotics, 4, 2019.

補足資料

この補足資料は、我々の研究へのさらなる洞察を提供します。付録Aでは、ネットワークアーキテクチャについてより詳細に説明します（付録Aは必然的にセクション3と重複します）。さらに、付録A.1では、UniK3Dの複雑さを分析し、他の手法と比較します。また、付録A.2では、設計上の選択肢に加えて、それらについてさらに詳しく説明します。付録Bでは、付録B.1で選択されたトレーニングパイプラインとハイパーパラメータの概要を示します。付録B.2では、トレーニングデータと検証データ、付録B.3では、完全性と再現性を確保するためのカメラ拡張について説明します。さらに、付録Cでは、付録C.2で、データセットごとの評価によるより詳細な定量的評価を提供します。KITTIとNYUv2で微調整されたUniK3Dに対応する結果は、付録C.1で報告されています。付録Dでは、発生する可能性のある質問への回答を示します。最終的には、追加の視覚化が付録Eに提供されます。

A. アーキテクチャー

エンコーダー　本モデルアーキテクチャでは、Vision Transformer (ViT) [15] をエンコーダーとして採用し、SmallからLargeまでの様々なスケールでその有効性を実証しています。ViTバックボーンは元々分類タスク用に開発されたため、最終の3層（プーリング層、全結合層、ソフトマックス層）を削除して修正しました。修正されたViTバックボーンの最後の4層から特徴マップとクラストークンを抽出します。これらの出力はLayerNorm [4] を用いて平坦化され、処理された後、線形投影層で処理されます。線形層は、特徴とクラストークンを共通のチャネル次元にマッピングします。このチャネル次元は、Large、Base、SmallのViTバリアントに対してそれぞれ512、384、256に設定されています。重要なのは、正規化層と線形層の重みはそれぞれ独立しており、異なる特徴解像度とクラストークン間で共有されないことです。その後、高密度特徴マップはRadialモジュールに渡され、クラストークンはAngularモジュールに送られます。

角度モジュール　エンコーダーから抽出された4つのクラストークンは、まずそれぞれ3次元、3次元、5次元、7次元に投影されます。次に、チャネル次元dに基づいてチャンクに分割され、サイズ3、3、5、7のトークングループが生成されます。これらのトークングループは、それぞれ1次、2次、3次の球面調和関数（SH）係数を表すドメイントークンの初期化として機能します。合計18個のトークン（T）があり、Transformer Encoderの2層で処理されます。各Transformer Encoder層は、8つのヘッドを持つ自己注意と、4C次元の単一の隠れ層を持ち、ガウス誤差線形ユニット（GELU）活性化関数を使用する多層パーセプトロン（MLP）で構成されています[26]。自己注意層とMLP層はどちらも、学習の安定性を向上させるために残差接続を含んでいます。18個のトークンはそれぞれスカラー次元に投影されます。最初の3つのトークンは、球面調和関数のドメインを具体的に定義します。最初のトークンは水平視野角(HFov)を決定し、\(2π · σ(\mathbf T_0)\)として計算されます。ここで、σはシグモイド関数を表します。2番目と3番目のトークンは、球面調和関数の極、つまり画像形状に対する投影の中心を表し、それぞれ\(c_x = \frac{σ(\mathbf T_1)W}{2}\)と\(c_y = \frac{σ(\mathbf T_2)H}{2}\)として計算されます。ここで、\(H\)と\(W\)は画像の高さと幅です。垂直FoVは、正方形ピクセルの仮定の下で導出されます：\(HFov × \frac{H}{W}\)。この領域定義を用いて、定数成分を除いた3次までの球面調和関数を計算し、サイズ\(\mathbb R^{H×W×3}\)の15個の調和テンソルを生成します。光線束\(\mathbf C\)は、これらの調和関数と対応する15個の処理済みトークン(T3:18)の線形結合として構築されます。

ラジアルモジュール　正弦波エンコードされたカメラレイ \(\mathbf C\) は、Transformer Decoder 層を介して、高密度特徴マップの各解像度レベル \(\mathbf F\) を調整するために使用されます。この設定では、高密度特徴 \(\mathbf F\) がクエリとして機能し、正弦波エンコードされたカメラレイがキーと値を提供します。クロスアテンションメカニズムには、LayerScale などの学習可能なゲイン係数のない残差接続が含まれます。調整された特徴は、特徴ピラミッドネットワーク (FPN) 方式で洗練されます。最も深い特徴は、2 つの残差畳み込みブロック [25] を経て処理され、その後、双線形アップサンプリングと、チャネル次元を半分にする投影ステップが続きます。これらのアップサンプリングされた特徴は、次の層の特徴と結合されます。これらの特徴も同様にチャネル次元に一致するように投影され、単一の2x2転置畳み込みを使用してアップサンプリングされます。このプロセスは、残りの3つの特徴マップがすべて消費されるまで続きます。最終的な出力特徴は入力画像の解像度にアップサンプリングされ、単一チャネル次元に投影され、対数半径\(\mathbf R_{log}\)が生成されます。アーキテクチャ的には同じ投影ですが、重みは別々に使用され、対数信頼度\(Σ_{log}\)が生成されます。最終的な半径と信頼度の値は、これらのテンソルを要素ごとに累乗し、対数空間から元の空間に変換することで得られます。

A.1. 複雑度

UniK3Dの計算コストを詳細に分析し、表7に示す他の最先端手法と比較します。公平で一貫性のある比較を行うため、すべてのモデルで可能な限り同じ入力サイズを使用します。しかし、このアプローチにはいくつかの課題があります。例えば、DepthProはエンタングルド構造とマルチ解像度アーキテクチャを採用しているため、手法間で入力サイズを一貫して調整することが複雑です。そのアーキテクチャ設計では調整が容易ではなく、標準化された入力サイズに合わせることが困難です。さらに、第4章の主な実験で評価したDepthProやMetric3Dなどのモデルのパフォーマンスは、トレーニング中に使用した画像形状とは異なる画像形状でテストした場合、大幅に低下します。この感度は根本的な限界を浮き彫りにしています。これらの手法は特定の画像解像度に最適化されており、これらの解像度から逸脱すると、パフォーマンスが大幅に低下する可能性があります。したがって、最も公平な条件下で計算を測定するよう努める一方で、これらのモデルはトレーニング設定とは異なる解像度には適していないことを認識することが重要です。対照的に、UniK3Dは画像の形状に対して柔軟に対応できるように設計されており、さまざまな解像度で堅牢なパフォーマンスを維持します。実験では、計算効率とパフォーマンスのバランスの取れたトレードオフを提供するため、DepthAnything v2と同じ入力形状を選択しました。さらに、CUDAカーネルスレッドの非同期性を考慮するため、適切な同期を有効にし、CUDAイベント記録を利用することで、正確な推論時間測定を保証します。このアプローチにより、計算コストを正確に反映し、非同期操作による誤った表現を回避できます。表7に示すように、UniK3Dは最も効率的なモデルの1つです。特にDepthAnything v2と比較した場合の計算コストの主な違いは、AngularモジュールとScaleコンポーネントが含まれていることに起因しています。これらのコンポーネントは、絶対的なメトリック深度とカメラ固有の調整をモデルが処理するために不可欠です。これらの機能は、相対的な深度推定ネットワークでは必要とされません。この追加の複雑さにもかかわらず、モデルの効率は競争力を維持しており、高性能を維持しながら多様なカメラ形状に対応する設計の有効性を強調しています。

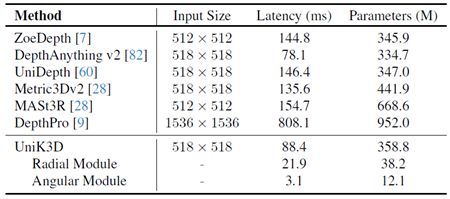
表7. パラメータと効率の比較。入力サイズ、レイテンシ、学習可能なパラメータ数に基づく手法のパフォーマンス比較。RTX3090 GPU、16ビット精度浮動小数点数、同期タイマーでテスト。最後の2行は、個別に評価されたAngularモジュールとRadialモジュールに対応しています。すべてのモデルはViT-Lバックボーンに基づいています。

A.2. アーキテクチャの代替案

UniDepth [60] ではカメラコンディショニングが優れていることが証明されているにもかかわらず、Transformer EncoderとDecoderの両方のコンポーネントについて、代替アーキテクチャの選択肢を除外する。特に、コンディショニングには最も一般的な代替手法、すなわち単純な加算または連結を選択した。カメラトークン処理の「代替」には、カメラトークンを最終的な投影層にショートカットするアイデンティティが含まれる。表9は、エンコーダ層を介したカメラトークン処理が大きな変化を示さないことを示しており、異なる層のクラストークンが既に有益であることがわかる。しかし、表8は、加算や連結などのより単純なコンディショニングの代替手法が、注意に基づくコンディショニングよりもパフォーマンスが低いことを明確に示している。これは、コンディショニングが最終的なパフォーマンスに重要な役割を果たし、適切に設計されたコンディショニングが適切な一般化を達成する上でいかに重要であるかを強調している。

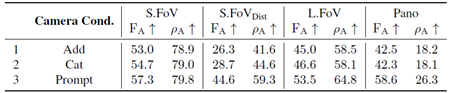
表8. カメラコンディショニング設計におけるアブレーション。カメラコンディショニングは、カメラの特徴を用いて深度特徴をコンディショニングするために用いられるカメラコンディショニングの種類に対応する。Addは特徴空間における単純な加算を指す。Catは2Cチャネル次元からCチャネル次元への単純な連結と射影を表す。Promptは注意に基づくコンディショニングである。

表9. カメラトークン処理に関するアブレーション。T-Enc. は、カメラトークンがAngularモジュールでトランスフォーマーエンコーダーレイヤーを介して処理されるかどうかを示します。後者の場合、トークンは最終投影に直接送られます。

B. トレーニングの詳細

B.1. ハイパーパラメータ

学習パラメータ（最適化、スケジューリング、拡張）については表10にまとめています。利用された損失、入力値、および対応する重みについては表11にまとめています。

表10. トレーニングハイパーパラメータ。対応する値を持つすべてのトレーニングハイパーパラメータが示されています。

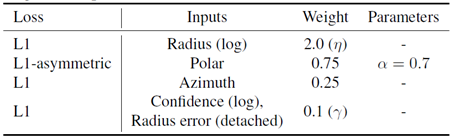
表11. トレーニング損失。対応する重みと入力値を伴うトレーニング損失。

B.2. データ

トレーニングデータセットと検証データセットの詳細は、表12と表13に示されています。

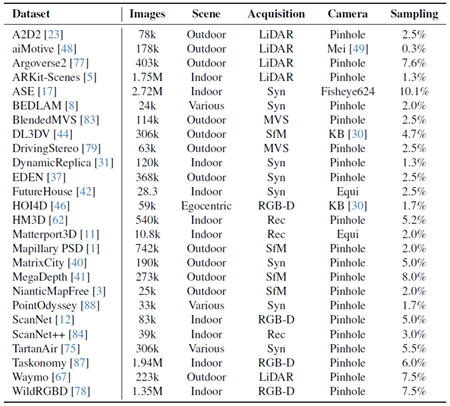
表12. 学習データセット。検証データセットのリスト：画像数、シーンタイプ、取得方法、サンプリング周波数が報告されています。SfM：Structure-from-Motion、MVS：Multi-View Stereo、Syn：Synthetic、Rec：Mesh Reconstruction、KB：Kannala-Brandt [30]、Equi：Equirectangular

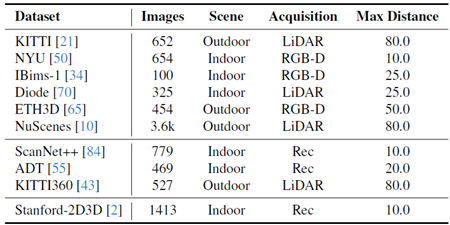
表13. 検証データセット。検証データセットのリスト：画像数、シーンタイプ、取得方法、最大評価距離が報告されています。第1グループ：小視野角、第2グループ：大視野角、第3グループ：パノラマ。Rec：メッシュ再構築。

トレーニングデータセット　トレーニングに使用されるデータセットは、表12に示すように、異なるカメラとドメインが混在しています。シーケンスベースのデータセットは、収集中に、連続する2つのフレーム間の間隔が0.5秒以上になるようにサブサンプリングされます。後処理は適用されません。トレーニングサンプルの総量は800万サンプルを超えます。データセットは、表12のサンプリング列の値に対応する確率で各バッチでサンプリングされます。この確率は、各データセットに含まれるシーンの数に関連しています。ただし、確率は単純な定性データ検査に基づいて変更されるため、最も多様なデータセットがより多くサンプリングされます。データセットのほとんどは、ピンホール画像または偏向カメラ（例： MegaDepth [41] や NianticMapFree [3] などのデータセットでは、明らかに歪んでいるにもかかわらず、ピンホールキャリブレーションのみを提供しています。例えば Mapillary [1] では、カメラ損失の計算においてサンプル全体がマスクされています。

検証データセット　表13は、すべての検証データセットを示し、それらを3つのグループ（小視野角、大視野角、パノラマ）に分割しています。標準的な方法に従い、KITTI Eigensplitは、元の697枚の画像から不正確なGTを除外した45枚の画像で補正および累積されたGT深度マップに対応しています。評価に使用した、セクション3で示した歪みのある小視野角は、ETH3D、Diode（屋内）、IBims-1の合成カメラに基づいて取得されています。すべての歪み画像とカメラは、付録B.3に示すパイプラインで生成された後、手動でリアリティがチェックされています。

B.3. カメラの拡張

歪んだカメラデータの多様性が限られていることに対処するため、ピンホールカメラで撮影した画像を人工的に変形することで拡張し、Fisheye624やラジアルKannala-Brandt [30]などの歪んだカメラモデルの画像をシミュレートします。拡張プロセスには主に2つのステップがあります。まず、変形フィールドを計算します。これは、ピンホールカメラから取得した2D深度マップを3D点群に逆投影することから始まります。次に、これらの3D点をランダムにサンプリングした歪んだカメラモデルの画像平面に投影し、新しい2D座標を取得します。変形フィールドは、元の2D画像座標と新しく投影された2D座標間の距離として定義されます。このフローは、歪んだカメラビューの外観を模倣するために元の画像をどのように変形する必要があるかを示しています。次に、ソフトマックスベースのスプラッティング[66]を用いて画像をワーピングします。これは、画像の詳細を維持しながら、計算された変形フィールドに基づいてピクセルを投影する手法です。ワーピング処理によって穴などのアーティファクトが生成されないようにするために、各ピクセルの深度値の逆数である「重要度」メトリックを使用します。このメトリックは近い点を優先し、ワーピング中に詳細と正しい視差が維持されるようにします。正解深度マップが利用できない非合成画像の場合は、推論のみのモードで深度予測を生成し、変形を計算します。これらの予測がリアルな変形を作成するのに十分な精度であることを保証するために、モデルが10,000ステップ学習された後にのみ、この拡張を適用します。この時点で、モデルは十分に信頼できる（スケール不変の）深度表現を学習しています。新しいランダムカメラをサンプリングするために使用された特定のカメラパラメータは、表15に示されています。

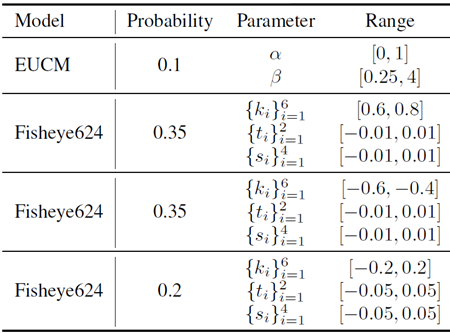
表14. S.FoVDist生成のためのカメラサンプリング。S.FoVDist画像を生成するためのパラメータを列挙する。パラメータ範囲の異なる複数のカメラモデルを使用した。サンプリングは、範囲内で均一サンプリングで行われる。シード値は13である。

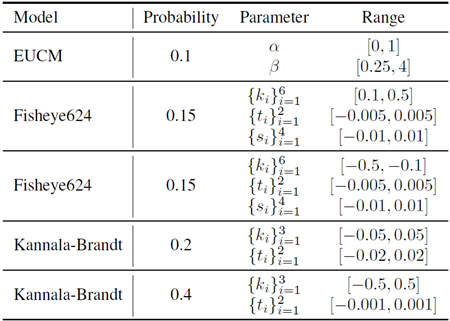
表15. カメラ拡張のためのカメラサンプリング。学習画像中に拡張カメラを生成するためのパラメータを記載しています。パラメータ範囲の異なる複数のカメラモデルを使用しました。サンプリングは、範囲内で均一に行われます。記載されていないパラメータ（例：Kannala-Brandtモデルの場合、{ki}6i =4）は0に設定されます。

検証データセットの生成　視野が狭くなった歪んだ画像でモデルをテストするための検証データセットを生成することは、多くの歪みが通常広い視野に関連しているため、さらなる課題を伴います。これをシミュレートするために、ETH3D [65]、IBims-1 [34]、Diode (Indoor) [70] などのデータセットから合成カメラパラメータを使用してRGB画像を変形します。これらのデータセットを選択した理由は、ほぼ完全な正解深度マップを提供するため、変形プロセスが適切かつ現実的になるためです。深度マップの小さなギャップや穴は、インペインティングを使用して埋められます。重要なのは、3D正解データは、使用するカメラモデルに対して不変であるため、変更されないことです。現実感を保証するために、各変形画像を手動で検証し、データ生成コードと結果の検証データの両方を公開します。

C. 追加の定量的結果

C.1. 微調整

UniK3Dの微調整能力を評価するため、KITTIまたはNYUのいずれかを唯一の学習データセットとして学習を再開する。微調整プロセスは、大規模な事前学習フェーズ後に得られた重みと最適化状態から開始され、公平かつ一貫性のある初期化を保証する。学習目標には標準的なSILog損失を使用し、バッチサイズは16とし、モデルはさらに40,000ステップ学習する。評価をドメイン内データの影響に焦点を絞るため、水平反転以外のすべての拡張を無効にし、微調整中は角度損失の非対称成分を省略する。評価では、先行研究との比較可能性を確保するために、両方のデータセットの標準的な手法に従う。 KITTIの結果はGarg [20]の評価クロップを用いて報告されており、KITTIとNYUの最大評価深度はそれぞれ80メートルと10メートルに設定されています。重要な点として、一貫性を維持し、追加の交絡因子の導入を回避するために、入力サイズの変更などのテスト時の拡張やチューニングは適用していません。結果は、UniK3Dがドメイン内微調整から大幅に恩恵を受けることを示しています。表17は、UniK3Dが本質的に柔軟性とドメイン間の一般化を目的として設計されているにもかかわらず、KITTIのような高度に構造化され較正されたデータセットで非常に優れたパフォーマンスを発揮するモデルの能力を示しています。これは、微調整を行うことで、モデルが適切に構造化されたデータに効果的に適応できることを示唆しています。この微調整分析は、柔軟性を重視した設計を維持しながら、UniK3Dがさまざまな設定に適応できることを強調しています。同様に、表16は、典型的な屋内環境を表すNYUのような構造化されていないドメインで微調整した場合でも、UniK3Dが競争力を維持することを示しています。これらの結果は、特に異なる特性を持つデータセットやドメイン固有の課題を持つデータセットにおいて、最適なパフォーマンスを達成するためにドメイン内データの重要性を裏付けています。さらに、この結果は、大きく異なるデータセット特性にわたって優れたパフォーマンスを達成しており、モデルの堅牢性を強調しています。

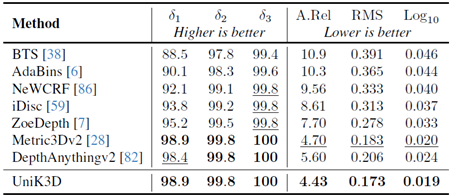
表16. NYU検証セットでの比較。すべてのモデルはNYUで学習されています。最初の4つのモデルはNYUでのみ学習されています。最後の4つのモデルはNYUで微調整されています。

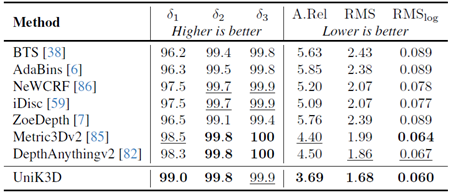
表17. KITTI Eigen-split検証セットにおける比較。すべてのモデルはKITTI Eigen-splitトレーニングで学習され、対応する検証セットでテストされています。最初のモデルはKITTIのみで学習されています。最後の4つはKITTIで微調整されています。

C.2. データセットごとの評価

各検証データセットの結果を、表18 (NYUv2)、表19 (KITTI)、表20 (IBims-1)、表21 (ETH3D)、表22 (Diode Indoor)、表23 (nuScenes)、表24 (IBims-1Dist)、表25 (ETH3DDist)、表26 (Diode IndoorDist)、表27 (ScanNet++ DSLR)、表28 (ADT)、および表29 (KITTI360) に個別に示します。「Pano」グループはStanford-2D3Dという単一のデータセットのみで構成されているため、このグループの結果は報告していません。この結果から、ピンホールカメラモデルのパフォーマンスは飽和点に達しているものの、UniK3Dはすべてのデータセットで常に1位にランクされているわけではないものの、全体的に最も高い平均指標を達成していることがわかります。これは、UniK3Dの強力な汎化能力を示すものです。これは、柔軟な設計と大規模な学習によって実現され、特定の領域に過剰適合することなく、多様な領域にわたって堅牢なパフォーマンスを実現します。さらに、A.Rel（パーセンテージ）で表される絶対相対誤差や、メートルを単位とする二乗平均平方根誤差（RSME）など、より一般的な指標も報告します。

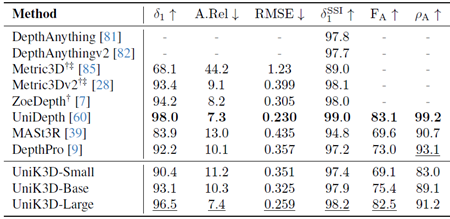
表18. NYUv2のゼロショット評価の比較。欠損値(-)は、モデルがそれぞれの出力を生成できないことを示します。†: 3D再構成用の正解カメラ。‡: 2D深度マップ推論用の正解カメラ。

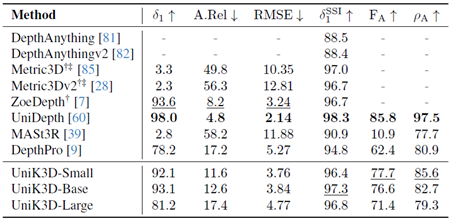
表19. KITTIのゼロショット評価の比較。欠損値（-）は、モデルがそれぞれの出力を生成できないことを示します。†：3D再構成用の正解カメラ。‡：2D深度マップ推論用の正解カメラ。

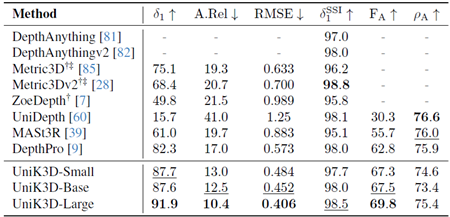
表20. IBims-1のゼロショット評価の比較。欠損値（-）は、モデルがそれぞれの出力を生成できないことを示します。†：3D再構成用の正解カメラ。‡：2D深度マップ推論用の正解カメラ。

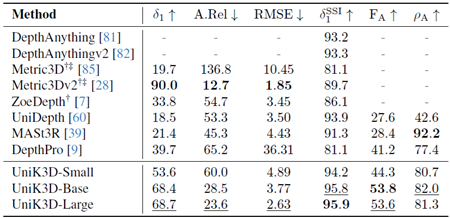
表21. ETH3Dのゼロショット評価の比較。欠損値（-）は、モデルがそれぞれの出力を生成できないことを示します。†：3D再構成用の正解カメラ。‡：2D深度マップ推論用の正解カメラ。

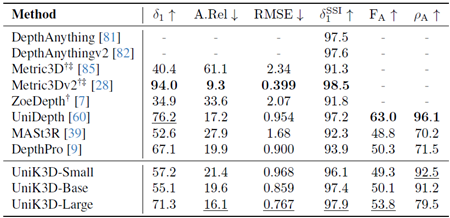
表22. ダイオード（屋内）のゼロショット評価の比較。欠損値（-）は、モデルがそれぞれの出力を生成できないことを示します。†：3D再構成用の正解カメラ。 ‡：2D深度マップ推論用の正解カメラ。

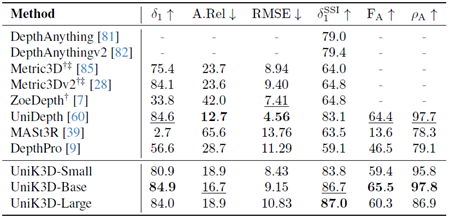
表23. nuScenesのゼロショット評価の比較。欠損値（-）は、モデルがそれぞれの出力を生成できないことを示します。†：3D再構成用の正解カメラ。‡：2D深度マップ推論用の正解カメラ。

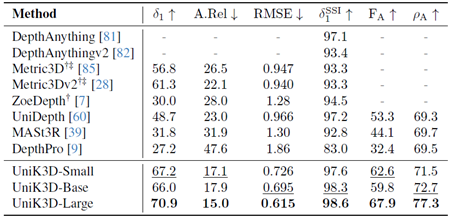
表24. IBims-1Distのゼロショット評価の比較欠損値（-）は、モデルがそれぞれの出力を生成できないことを示します。†：3D再構成用の正解カメラ。‡：2D深度マップ推論用の正解カメラ。

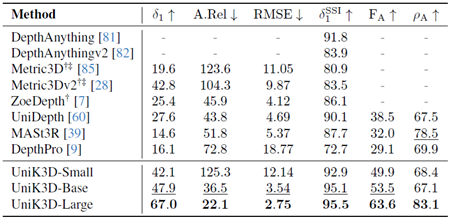
表25. ETH3DDistのゼロショット評価の比較。欠損値（-）は、モデルがそれぞれの出力を生成できないことを示します。†：3D再構成用の正解カメラ。‡：2D深度マップ推論用の正解カメラ。

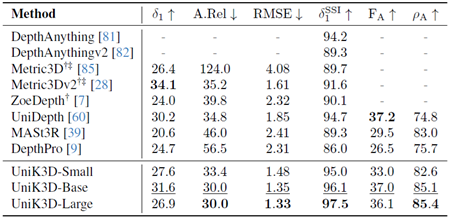
表26. DiodeDist（屋内）のゼロショット評価の比較。欠損値（-）は、モデルがそれぞれの出力を生成できないことを示します。†：3D再構成用の正解カメラ。 ‡：2D深度マップ推論用の正解カメラ。

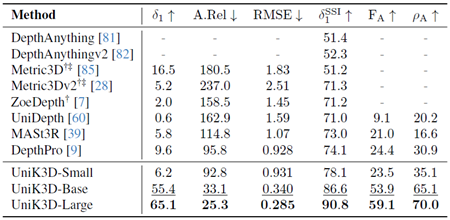
表27. ScanNet++(DSLR)のゼロショット評価の比較。欠損値(-)は、モデルがそれぞれの出力を生成できないことを示します。†: 3D再構成用の正解カメラ。 ‡: 2D深度マップ推論用の正解カメラ。

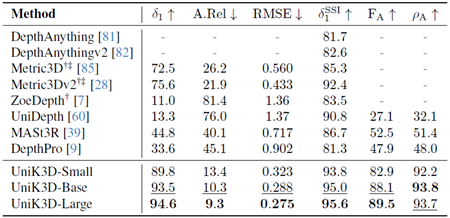
表28. ADTのゼロショット評価の比較。欠損値（-）は、モデルがそれぞれの出力を生成できないことを示します。†：3D再構成用の正解カメラ。‡：2D深度マップ推論用の正解カメラ。

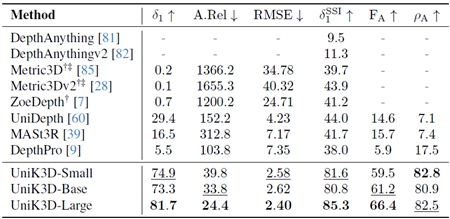
表29. KITTI360のゼロショット評価の比較。欠損値（-）は、モデルがそれぞれの出力を生成できないことを示します。†：3D再構成用の正解カメラ。‡：2D深度マップ推論用の正解カメラ。

D. Q&A

ここでは、論文を読んだ後に生じる可能性のある疑問を列挙します。このセクションは、討論的な質疑応答形式で構成されています。

• シーンスケールに関する一般化において、データの重要性はどの程度ですか？
　データの多様性は、深度推定の一般化において極めて重要です。特に、意味的手がかりに大きく依存し、ドメインギャップの影響を受けやすい単眼手法においては重要です。単眼メトリック深度推定におけるスケール予測は本質的に不適正であり、学習ドメインとその分布カバレッジに大きく依存します。KITTIのような狭く特殊なドメインでは、過度の多様性はパフォーマンスを低下させる可能性があります。大規模で多様なデータセットで学習されたモデルは、ドメイン固有のデータで学習されたモデルと比較して、パフォーマンスが低下することがよくあります。逆に、これらのモデルはNYUのようなより広範なドメインでは優れたパフォーマンスを発揮します。スケール予測は通常、ノイズが多く、ドメインシフトの影響を受けやすいですが、この問題はドメイン内微調整によって軽減できます。例えば、KITTI で微調整を行う際、数百ステップの最適化で「スケールギャップ」をほぼ解消できます。
• カメラ表現はピンホールカメラモデルや完全にノンパラメトリックなカメラモデルよりも優れていますが、一般的なカメラモデルと比較していません。なぜでしょうか？
　当初は明示的なパラメトリックカメラモデルを試しましたが、重大な欠点に遭遇しました。ほとんどの標準的なカメラモデルは、微分不可能なバックプロジェクション演算に依存しているため、標準的なディープラーニングパイプラインでは使用できません。この制限に対処するには、(i) EUCM [33] や DoubleSphere [69] などの微分可能なパラメトリックモデルを使用するか、(ii) 微分可能な関数で多項式逆変換を近似するか、(iii) カメラを直接監視せずにモデルパラメータのみを監視するかのいずれかが必要です。これらのアプローチはすべて、パラメトリックモデルに固有の不安定性という問題を抱えています。パラメトリックモデルでは、パラメータの変化は実際の出力、つまり光線束と合わせて考慮する必要があります。この小さな変化の積み重ねが大きな出力変化につながるという相乗効果は、しばしば不安定な最適化につながります。さらに、パラメトリックモデルは逆投影演算の表現力を制限し、モデルが表現できるカメラのみに適用範囲を限定します。これに対し、私たちの表現はこれらの制限を回避し、より高い柔軟性と安定性を提供します。

• DUSt3R / MASt3Rアーキテクチャはポイントマップを直接予測しますが、一般的なカメラでは機能しないのでしょうか？
DUSt3RおよびMASt3Rネットワークは理論的にはあらゆるカメラモデルを表現できますが、私たちの研究では、完全にノンパラメトリックなアプローチは、多様なデータセットで学習させ、エッジケースや分布の裾野でテストした場合に困難をきたすことが明らかになりました。さらに、DUSt3R [74] および MASt3R [39] で使用されるテスト時の点群グローバルアライメント手法は、ピンホールカメラを明示的に必要とするため、汎用カメラへの適用がさらに制限されます。

• 信頼性予測の役割は何ですか？
　信頼性予測は、主に下流タスクでの有用性とレガシーシステムの都合上、組み込まれています。ほとんどの回帰タスクと同様に、信頼性予測はドメインギャップの影響を受けやすく、ドメイン外の強いシナリオでは信頼性が低下する可能性があることに注意する必要があります。

• カメラ拡張の根拠は何ですか？
　カメラ拡張は、多様な実カメラデータの不足に対処するために採用されました。シンプルな拡張パイプラインはわずかな改善をもたらしましたが、生成されたカメラの多くは非現実的であり、現実世界のカメラの分布から外れていることがわかりました。しかし、ソフトマックスベースのワーピングは現実的な画像の作成に効果的であることが証明されました。特定のパラメータではなく出力光線の現実性を考慮した、より洗練されたカメラサンプリング手順は、現実の実用的なカメラモデル全体にわたる堅牢性と一般化を大幅に向上させる可能性があると仮説を立てています。

• UniDepth との違いは何ですか？
UniDepth [60] と UniK3D はカメラモデリングと 3D 表現において異なり、これらは表 3、4、5 で詳しく説明されています。 UniDepth はキャリブレーション行列を予測することでピンホールモデルに依存しているため（[60、3.2 節] を参照）、カメラを予測することはできません。さらに、[60] は 3 次元目を深度 (z) として表現しています [60、3.1 節]。これらの 2 つの特徴により、[60] はピンホールのみをモデル化し、FoV が 180◦ 未満となるように出力します。一方、UniK3D は球面調和関数 (SH) を使用してあらゆるカメラモデルを近似し、半径距離 (r) を 3 次元目として利用します。UniDepth は予測されたピンホール光線マップを投影します [60、3.2 節]。 3.1] を高次元空間 E にSHを用いて投影するのに対し、UniK3D は逆変換 (L230-262) を用いてレイマップ C を生成する際に使用するSH係数を直接予測します。この重要な方法論的違いは、あらゆるカメラのモデリングにつながります。表30 (行1と行3) はその影響を示しています。UniK3D は、同一データで学習させた場合でも、一貫して [60] よりも優れた性能を示しています。

• これまでに同様の研究を行った人はいますか？
　はい、深度推定におけるピンホール仮定を排除しようとした研究がいくつかあります [27, 35]。しかし、それらは2つの重要な理由で異なります。(i) これらの研究は単一領域のシナリオに焦点を当てているため、設定が単純化されていること、(ii) タスクが自己教師あり深度推定であること、そしてカメラはワーピングベースの測光損失を定義するために必要であり、教師ありの大規模な単眼3D推定ではないことです。

• 表5の3行目と4行目の\(δ_1^{SSI}\)スコアはそれぞれ92.1と92.2です。このスコアの類似性は、\(F_A\)と\(ρ_A\)の低下（表5）とともに、角度モジュールの役割を浮き彫りにしています。実際、ラジアルベースおよびSHベースのモデル（4行目）は、レンズ歪みのある画像のFoVを過大評価します。狭いFoVに対してより強い歪み増強を施した再学習を行うと、(\(F_A, ρ_A\)) = (43.1, 62.3)となり、仮定が検証されます。

表30. UniDepthとの比較。すべてのモデルはViT-Sバックボーンと同じ学習データを使用しています。テストセットのグループ化は本論文と同じです。画面上で拡大表示すると最適です。

E. 追加の定性的な結果

ここでは、特に本論文では示されていない検証ドメインと、歪んだカメラを用いた、より定性的な比較を図5に示します。具体的には、ScanNet++（DSLR）、IBims-1Dist、DiodeDist（屋内）です（図5）。さらに、映画、テレビシリーズ、YouTube、アニメなどのフレームなど、実際の状況で実際に存在するシナリオでモデルをテストします。図6と図7に示されているすべての画像は、歪んだカメラや通常とは異なる視点を示しています。ここで示す可視化は、検証セットと実際のセットの両方からランダムに選択されたものであり、厳選されたものではありません。

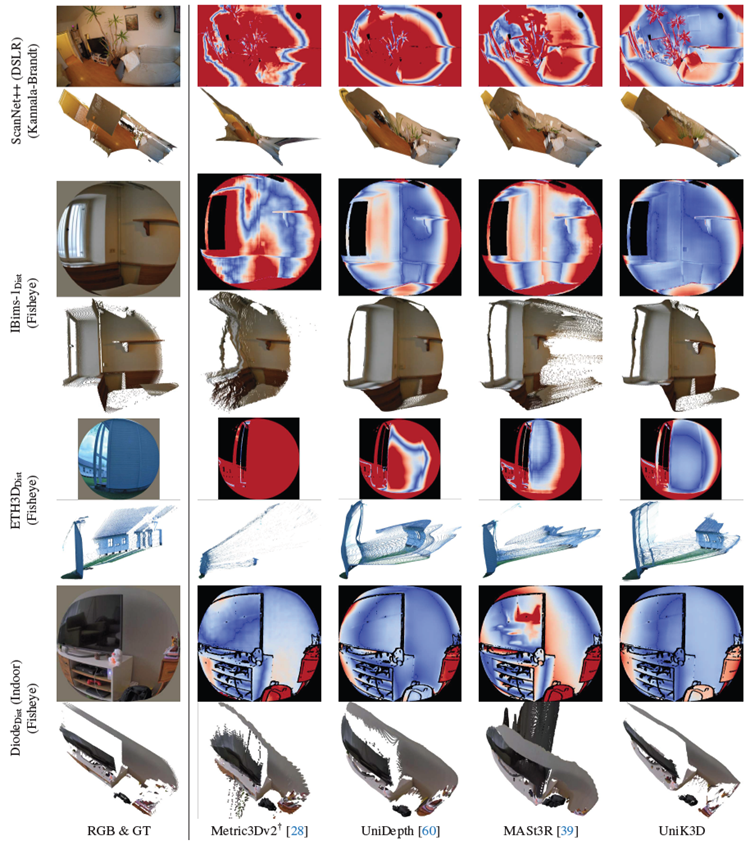
図5. 定性的な比較。連続する2つの行はそれぞれ1つのテストサンプルを表します。奇数行には入力RGB画像と2Dエラーマップが表示され、絶対相対誤差に基づいてクールウォームカラーマップで色分けされています。青は0%の誤差、赤は25%の誤差に対応しています。公平な比較を行うため、すべてのモデルについて、GTベースのシフトおよびスケーリングされた出力に基づいて誤差が計算されています。偶数行には3D点群の正解と予測値が表示されます。すべてのサンプルはランダムに選択されており、抜き出しは行われていません。†：GTカメラの逆投影。

図6. 定性的な3D実世界結果。UniK3Dは左列の各画像を単独で入力し、対応する点群を右列に出力します。3Dをより分かりやすくするために、視点は少し傾けられています。画像はそれぞれ、Poor Things（映画）、The Revenant（映画）、Eminem（ミュージックビデオ）、YouTube（自己中心的なGoPro）のビデオフレームです。フレームには、様々なカメラタイプと珍しい視点が映し出されています。

図7. 定性的な実環境3D結果。UniK3Dは左列の各画像を単独で入力し、対応する点群を右列に出力します。3Dをより分かりやすくするために、視点は少し傾けられています。画像はそれぞれ、トレインスポッティング（映画）、YouTube（ドアベルカメラ）、NARUTO（アニメ）、ブレイキング・バッド（テレビシリーズ）のビデオフレームです。フレームには、様々なカメラタイプと珍しい視点が映し出されています。

UniK3D: Universal Camera Monocular 3D Estimation

要旨