近年の最前線の言語モデルでは、解答を出す前に詳細な思考プロセスを生成する大規模推論モデル(LRM:Large Reasoning Models)が導入されている。これらのモデルは推論ベンチマークで性能向上を示しているものの、その基本的能力、スケーリング特性、限界については未だ十分に解明されていない。現在の評価は主に確立された数学的およびコーディングベンチマークに焦点を当てており、最終的な解答の精度を重視している。しかし、この評価パラダイムはデータ汚染の影響を受けやすく、推論の痕跡の構造や質に関する知見が得られない。本研究では、制御可能なパズル環境を用いてこれらのギャップを体系的に調査する。この環境は、一貫した論理構造を維持しながら、構成上の複雑さを正確に操作することを可能にする。この設定により、最終的な解答だけでなく内部の推論の痕跡も分析できるようになり、LRMがどのように「考える」かについての知見が得られる。多様なパズルを対象とした広範な実験を通じて、フロンティアLRMは、ある一定の複雑さを超えると精度が完全に崩壊することを示す。さらに、それらは直感に反するスケーリング限界を示す。つまり、推論の努力は問題の複雑さとともにある点までは増加するが、その後は十分なトークン予算があるにもかかわらず減少する。同等の推論計算条件下で LRM を標準的な LLM と比較することにより、3 つのパフォーマンス状況を特定した。(1) 標準モデルが LRM より驚くほど優れている低複雑度のタスク、(2) LRM での追加思考が優位性を発揮する中複雑度のタスク、(3) 両方のモデルが完全に崩壊する高複雑度のタスク。LRM には正確な計算における限界があることがわかった。明示的なアルゴリズムを使用できず、パズル間で一貫して推論しない。また、推論のトレースをより詳細に調査し、探索されたソリューションのパターンを研究し、モデルの計算動作を分析して、その長所と限界を明らかにし、最終的にはその真の推論能力に関する重要な疑問を提起した。
大規模言語モデル(LLM)は近年進化を遂げ、推論タスク向けに明示的に設計された特化型、すなわちOpenAIのo1/o3 [1, 2]、DeepSeek-R1 [3]、Claude 3.7 Sonnet Thinking [4]、Gemini Thinking [5] などの大規模推論モデル(LRM)が含まれるようになりました。これらのモデルは、自己反省を伴う長い思考連鎖(CoT)などの「思考」メカニズムを特徴とする新しい成果物であり、様々な推論ベンチマークにおいて有望な結果を示しています。これらのモデルの出現は、LLMシステムが複雑な推論や問題解決タスクに取り組む方法に潜在的なパラダイムシフトをもたらすことを示唆しており、一部の研究者は、LLMをより汎用的な人工知能機能への重要なステップとして提案しています。

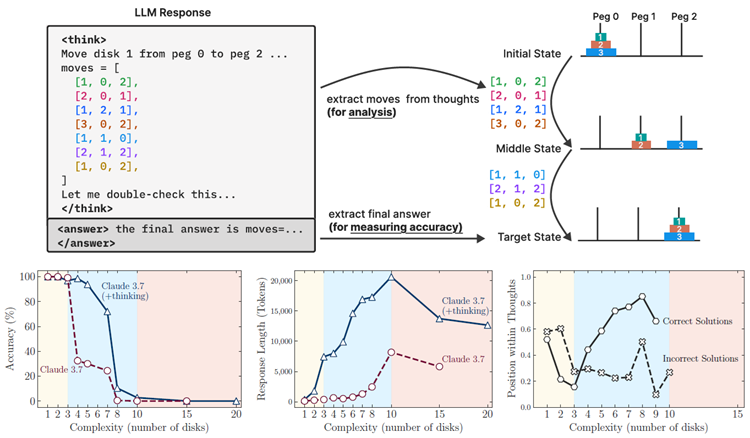
図 1: 上: この設定により、最終的な答えと中間の推論トレースの両方を検証できるため、モデルの思考動作を詳細に分析できます。下(左)と下(中央): 複雑度が低い場合、非思考モデルの方が精度が高く、トークン効率も高くなります。複雑度が増すにつれて、推論モデルの方がパフォーマンスが高くなりますが、より多くのトークンが必要になります。最終的には、どちらも臨界しきい値を超えてトレースが短くなります。下(右:) 正しく解決されたケースでは、Claude 3.7 の思考は、複雑度が低い場合は早く答えを見つけ、複雑度が高い場合は遅く答えを見つける傾向があります。失敗したケースでは、多くの場合、初期の間違った答えに固執し、残りのトークン バジェットを無駄にします。どちらのケースも、推論プロセスの非効率性を示しています。
こうした主張や性能向上にもかかわらず、LRMの根本的な利点と限界は依然として十分に理解されていない。重要な疑問は依然として残っている。これらのモデルは一般化可能な推論が可能なのか、それとも異なる形態のパターンマッチング[6]を活用しているだけなのか?問題の複雑さが増すにつれて、その性能はどのように変化するのか?同じ推論トークン計算を与えた場合、思考しない標準的なLLMモデルとどのように比較されるのか?最も重要なのは、現在の推論アプローチに内在する限界は何なのか、そしてより堅牢な推論能力を実現するためにはどのような改善が必要なのか、ということである。
これらの疑問を調査する体系的な分析が不足しているのは、現在の評価パラダイムの限界によるものだと考えています。既存の評価は主に、確立された数学的およびコーディング的ベンチマークに焦点を当てていますが、これらは有用ではあるものの、データ汚染の問題を抱えることが多く、異なる設定や複雑性において制御された実験条件を実現することができません。さらに、これらの評価では推論トレースの構造や品質に関する知見が得られません。これらのモデルの推論動作をより厳密に理解するには、制御された実験を可能にする環境が必要です。
本研究では、問題の複雑性という観点から、フロンティアLRMの推論メカニズムを検証する。標準的なベンチマーク(例えば数学問題)ではなく、制御可能なパズル環境を採用する。この環境において、パズルの要素を調整することで複雑性を体系的に変化させ、解と内部推論の両方を検証する(図1上)。これらのパズルは、(1)複雑性をきめ細かく制御できること、(2)既存のベンチマークによくある混入を回避できること、(3)明示的に提供されたルールのみを要求し、アルゴリズム的推論を重視できること、(4)シミュレータを用いた厳密な評価をサポートし、正確な解の検証と詳細な失敗分析を可能にすること、といった特徴を持つ。私たちの実証的調査により、現在の言語推論モデル (LRM) に関するいくつかの重要な発見が明らかになりました。第一に、強化学習によって学習された洗練された自己反省メカニズムにもかかわらず、これらのモデルは計画タスクのための一般化可能な問題解決能力を開発することができず、特定の複雑さのしきい値を超えるとパフォーマンスがゼロに低下します。第二に、同等の推論コンピューティング環境における LRM と標準的な LLM の比較により、3 つの異なる推論方式が明らかになりました (図 1 下部)。より単純で構成の少ない問題の場合、標準的な LLM は優れた効率と精度を示します。問題の複雑さが中程度に増加すると、思考モデルが有利になります。しかし、問題が高複雑度に達し、構成の深さが長くなると、両方のモデル タイプでパフォーマンスが完全に低下します (図 1 下部左)。特に、この低下点に近づくと、LRM は世代長の制限をはるかに下回って動作しているにもかかわらず、問題の複雑さが増加するにつれて推論の労力 (推論時間トークンで測定) を削減し始めます (図 1 下部中央)。これは、問題の複雑さに対するLRMの推論能力における根本的な推論時間スケーリングの限界を示唆しています。最後に、中間推論の痕跡または思考の分析により、複雑さに依存するパターンが明らかになりました。より単純な問題では、推論モデルはしばしば正しい解を早期に特定しますが、非効率的に誤った選択肢の探索を継続します。これは「考えすぎ」現象です。中程度の複雑さでは、正しい解は誤った経路を広範囲に探索した後にのみ出現します。特定の複雑さの閾値を超えると、モデルは正しい解を完全に見つけられなくなります(図1、右下)。これは、LRMが限られた自己修正能力しか持たないことを示しており、これは有用ではあるものの、根本的な非効率性と明確なスケーリング限界を露呈しています。
これらの研究結果は、既存のLRMの長所と限界の両方を浮き彫りにし、これらのシステムにおける推論の性質に関する疑問を提起し、その設計と展開に重要な示唆を与えています。私たちの主な貢献は以下のとおりです。
言語モデルにおける推論。大規模言語モデル(LLM)は、膨大な量のトレーニングデータを使用して、コストのかかる複数のトレーニング段階を経ます。これらのLLMは強力な圧縮機能により有望な言語理解を示していますが、その知能と推論能力は依然として科学的な議論の重要なトピックです[7, 8]。初期のLLM [9, 10, 11]は、推論ベンチマークで低いパフォーマンスを示しました[12, 13, 14, 6]。これらの欠点に対処するために、トレーニングデータとテスト時の計算の両方を「スケーリング」するという共通のテーマを持ついくつかのアプローチが検討されてきました。たとえば、思考の連鎖(CoT)[15, 16, 17, 18]を生成し、最終答えの前に自己検証を組み込む[19, 20, 21]と、モデルのパフォーマンスが向上することが示されています。しかし、高品質でスケーラブルな CoT データは希少であるため、入手コストが非常に高くなります。別の研究では、教師あり学習や強化学習 [22, 23, 24, 25, 26, 27] を通じてモデルがより効果的に考えるように教えることで、教師ありデータの不足を補うことに焦点を当てています。これらの改善の注目すべきオープンソースの例は Deepseek-R1 [3] で、検証可能な報酬を伴う RL を適用することでモデルのパフォーマンスが大幅に向上し、OpenAI の o1 [2] などのクローズドモデルに匹敵することを実証し、Gemini flash thinking [5]、Claude 3.7 Sonnet thinking [4] などの Large Reasoning Models (LRM) と呼ばれる新世代の言語モデルにつながっています。
大規模推論モデルを理解する。 最近の研究では、推論行動のさまざまな側面が調査されています。大規模推論モデルでは、思考の痕跡と最終的な答えの不一致 [28 , 29] などの新たな行動や、研究者が「考えすぎ現象」 [30 , 31 , 32 , 33] と呼ぶ効率性に関する懸念が示されています。つまり、モデルは解決策を見つけた後でも冗長で冗長な出力を生成し、推論の計算に大きなオーバーヘッドが生じます。この研究では、タスクの複雑さに関してモデルがどの程度考えるかを体系的に分析します。最近、Ballon ら [34] は、新しい LRM では数学の問題で思考が増加すると精度が一般的に低下するのに対し、制御されたパズル環境では難易度が一定のレベルを超えるとモデルがあまり考えなくなり、思考とタスクの複雑さの逆の相関関係はあるしきい値までしか起こらないことを実証しました。Yue ら [35] [35]は、強化学習が本当に新しい推論パターンを引き出すのかどうか疑問視し、推論モデルと非推論モデルのpass@kが同じ点に収束することを示しています。また、MATH-500では推論モデルと非推論モデルのpass@kは近いものの、パズルの難易度が中程度および高い場合では異なるパターンが見られ、これは一般的な評価に用いられる既存の数学ベンチマークでは容易に観察できません。
制御可能な評価環境。 言語モデルの推論能力を評価するために数学の問題に焦点を当てた以前の研究とは異なり、本研究では制御可能なパズル環境を導入します。これらの環境では、一貫した論理プロセスを維持しながら問題の複雑さを正確に操作できるため、推論パターンと制限のより厳密な分析が可能になります。制御可能な環境は文献では珍しくありません [12 , 36 , 37]。ただし、私たちの主な目的は新しいベンチマークを提案することではなく、言語モデルの推論能力を理解するための実験を設計するためのツールとしてこれらのベンチマークを使用します。Valmeekam らによる密接に関連する研究 [38] では、o1 モデルが以前のモデルと比較して大幅なパフォーマンスの向上を示すことが実証されました。私たちの研究は、思考/非思考モデルのペア (例: DeepSeek-R1/V3、Claude 3.7 Sonnet の思考/非思考) を調べるなど、追加の洞察を提供します。さらに、LRM の推論の痕跡をより詳細に研究し、さまざまな複雑さのレベルにわたるさまざまな動作を明らかにしました。
近年のLRMの有望な結果は、重要な疑問を提起する。それは、これまで報告されてきたLLMの限界はどの程度改善されたのか、ということである。本研究では、これらのLRMの性能を単に測定するだけでなく、LRMが様々な複雑さの問題にどれほどうまく対処できるかを分析し、その推論プロセスの特性を検証する。
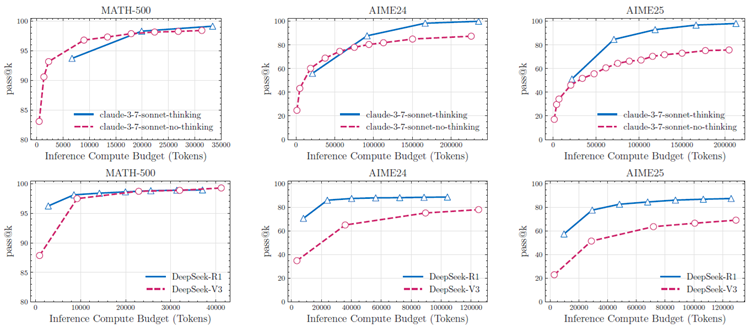
図2:数学ベンチマークにおける思考型モデルと非思考型モデルの比較分析では、一貫性のないパフォーマンスパターンが明らかになりました。MATH-500データセットの結果では、思考型モデルと非思考型モデルのパフォーマンスはほぼ同等でしたが、AIME24およびAIME25ベンチマークでは思考型モデルが優れたパフォーマンスを示しました。さらに、AIME24からAIME25へのベンチマークで観測されたパフォーマンスの低下は、これらのベンチマークがデータ汚染の問題に対して脆弱であることを浮き彫りにしています。
現在、最近のRLベースの思考モデルで観察されたパフォーマンスの向上が、確立された数学ベンチマークデータへの露出の増加に起因するのか、思考トークンに割り当てられた大幅に大きな推論計算に起因するのか、それともRLベースのトレーニングによって開発された推論能力に起因するのかは明らかではない。最近の研究[35、39]では、RLベースの思考モデルの上限機能(pass@k)を非思考の標準LLMの対応するものと比較することにより、確立された数学ベンチマークでこの問題を調査した。彼らは、同等の推論トークン予算の下で、非思考LLMは最終的にMATH500 [40]やAIME24 [41]などのベンチマークで思考モデルに匹敵するパフォーマンスに到達できることを示した。我々はまた、Claude-3.7-Sonnet(思考あり vs. 思考なし)やDeepSeek(R1 vs. V3)などの最先端のLRMの比較分析も行った。私たちの結果(図2に示す)は、MATH500データセットにおいて、同じ推論トークンバジェットを与えられた場合、思考モデルのpass@kパフォーマンスは非思考モデルのそれと同等であることを裏付けています。しかし、このパフォーマンスギャップはAIME24ベンチマークでは広がり、AIME25ではさらに広がることが分かりました。このギャップの拡大は解釈上の課題を提示します。これは、(1)複雑さが増すにつれてより洗練された推論プロセスが必要となり、より複雑な問題に対して思考モデルの真の利点が明らかになった、または(2)新しいベンチマーク(特にAIME25)でのデータ汚染が減少したことのいずれかに起因すると考えられます。興味深いことに、AIME25における人間のパフォーマンスは実際にはAIME24よりも高く[42, 43]、AIME25の方が複雑でない可能性があることを示唆しています。しかし、モデルはAIME25上ではAIME24よりもパフォーマンスが低く、これはフロンティアLRMのトレーニング中にデータ汚染が発生した可能性を示唆しています。これらの根拠のない観察と、数学のベンチマークでは問題の複雑さを制御された方法で操作できないという事実を考慮して、私たちはより正確で体系的な実験を可能にするパズル環境に目を向けました。
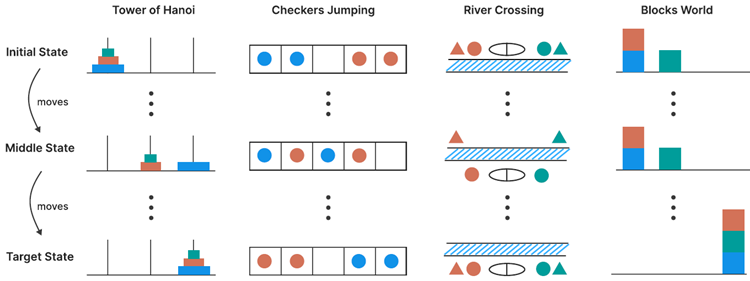
図3:4つのパズル環境の図解。列は、ハノイの塔(杭間のディスクの移動)、チェッカージャンプ(色付きトークンの位置交換)、川渡り(川を渡ってエンティティを移動)、ブロックワールド(スタックの再構成)の各パズルについて、初期状態(上)から中間状態(中)、目標状態(下)への進行を示しています。
我々は、構成の深さ、計画の複雑さ、および分配設定にまたがる4つの制御可能なパズルでLRM推論を評価します。パズルは以下に定義され、図3に示されています。ハノイの塔は、3つの杭と、最初の杭にサイズ順(一番大きいものが下)に積み重ねられたn個の異なるサイズのディスクを備えたパズルです。目標は、最初の杭から3番目の杭にすべてのディスクを移動することです。有効な動きには、一度に1枚のディスクのみを移動すること、杭から一番上のディスクのみを取ること、大きいディスクを小さいディスクの上に置かないことが挙げられます。このタスクの難易度は、初期ディスクの数によって制御できます。\(n\) 個の初期ディスクで必要な最小の動きの数は \(2n − 1\) になります。ただし、この研究では、最終解の最適性については評価せず、各動きの正確さと目標状態への到達のみを測定します。
チェッカージャンピング は、赤いチェッカー、青いチェッカー、そして1つの空きスペースを一列に並べる1次元パズルです。目的は、すべての赤と青のチェッカーの位置を入れ替え、最初の配置を反転させることです。有効な動きは、チェッカーを隣接する空きスペースにスライドさせるか、反対色のチェッカーを1つだけ飛び越えて空きスペースに着地することです。パズルの過程で、チェッカーを後方へ移動させることはできません。このタスクの複雑さはチェッカーの数によって制御できます。\(2n\) 個のチェッカーを使用する場合、必要な最小移動回数は \((n + 1)^2 - 1\) になります。
川渡り (River Crossing) は、\(n\) 人のアクターとそれに対応する \(n\) 人のエージェントがボートを使って川を渡る制約充足計画パズルです。目標は、\(2n\) 人の個体すべてを左岸から右岸に輸送することです。ボートは最大 k 人の個体を運ぶことができ、空のまま移動することはできません。アクターが他のエージェントの前にいるときに自分のエージェントがいないと、各エージェントは競合するエージェントからクライアントを保護する必要があるため、無効な状況が発生します。このタスクの複雑さは、存在するアクター/エージェントのペアの数によっても制御できます。\(n = 2、n = 3\) ペアの場合、ボートの定員は \(k = 2\) を使用し、ペアの数が多い場合は \(k = 3\) を使用します。
Blocks Worldは、ブロックを初期配置から指定された目標配置に並べ替えるブロック積み上げパズルです。この変形に必要な最小移動回数を見つけることが目的です。有効な移動は積み上げの最上部のブロックに限られ、積み上げられたブロックは空の積み上げか、他のブロックの上に置くことができます。この課題の難易度は、積み上げられるブロックの数によって調整できます。
私たちの実験のほとんどは、Claude 3.7 Sonnet(思考/非思考)やDeepSeek-R1 / V3などの推論モデルとその非思考モデルで行われています。これらのモデルを選択したのは、OpenAIのoシリーズなどのモデルとは異なり、思考トークンにアクセスできるためです。最終的な精度のみに焦点を当てた実験では、oシリーズモデルの結果も報告します。Claude 3.7 Sonnetモデルの場合、最大トークンバジェット(64k)を許可します。同様に、ローカルサーバー上のDeepSeek-R1 / V3モデルの場合、最大長を64kトークンまで許可します。各パズルインスタンスについて、25のサンプルを生成し、それらの各モデルの平均パフォーマンスを報告します。実験のセットアップと結果の包括的な詳細は、付録に記載されています。
図2の観察結果に基づき、問題の複雑さが推論行動に与える影響を体系的に調査するため、制御されたパズル環境において、思考型モデルと非思考型モデルのペアを比較する実験を行いました。分析は、同一のモデルバックボーンを持つLLMのペア、具体的にはClaude-3.7-Sonnet(思考あり vs. 思考なし)とDeepSeek(R1 vs. V3)に焦点を当てました。各パズルにおいて、問題サイズ \(N\)(ディスク数、チェッカー数、ブロック数、または交差要素を表す)を操作することで複雑さを変化させました。
図4は、すべてのパズル環境における問題の複雑さの関数として、両モデルの精度を示しています。これを補完する図5は、同等の推論トークン計算(すべてのパズルの平均)におけるこれらのモデルペアの上限性能能力(pass@k)を示しています。これは、数学ベンチマーク(図2)での以前の分析を、制御されたパズル環境に拡張したものです。これらの図の結果は、数学における観察とは異なり、複雑さに関するこれらのモデルの挙動には3つの領域が存在することを示しています。問題の複雑さが低い最初の領域では、非思考モデルは、よりトークン効率の高い推論を行う思考モデルと同等、あるいはそれ以上の性能を達成できることが観察されます。中程度の複雑さを持つ2番目の領域では、長い思考の連鎖を生成できる推論モデルの利点が現れ始め、モデルペア間の性能差が拡大します。最も興味深い領域は、問題の複雑さが高く、両モデルのパフォーマンスがゼロにまで低下した3番目の領域です。結果は、思考モデルがこの崩壊を遅らせる一方で、思考しないモデルと同じ基本的な限界に最終的に遭遇することを示しています。
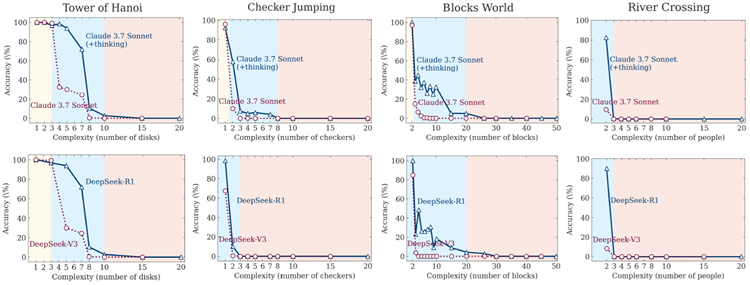
図 4: すべてのパズル環境とさまざまなレベルの問題の複雑さにおける、思考モデル (思考機能付き Claude 3.7 Sonnet、DeepSeek-R1) と非思考モデル (Claude 3.7 Sonnet、DeepSeek-V3) の精度の比較。
次に、思考トークンを備えたさまざまな特化型推論モデルが、増大する問題の複雑さにどのように対応するかを調べます。実験では、最先端の思考モデル o3-mini (中および高構成)、DeepSeek-R1、DeepSeek-R1-Qwen-32B、Claude-3.7-Sonnet (思考) の 5 つを評価します。図 6 は、さまざまな複雑さのレベルにわたって、精度 (上) と思考トークンの使用 (下) の観点からこれらのモデルのパフォーマンスを示しています。結果は、すべての推論モデルが複雑さに関して同様のパターンを示していることを示しています。つまり、問題の複雑さが増すにつれて精度は徐々に低下し、モデル固有の複雑さのしきい値を超えると完全に崩壊 (精度 0) します。推論思考トークン計算の分析では、これらのモデルによって学習された思考トークンの割り当てにおける興味深いパターンも明らかになりました。推論モデルは最初、問題の複雑さに比例して思考トークンを増加させることがわかります。しかし、臨界閾値(精度崩壊点にほぼ相当)に近づくと、モデルは直感に反して、問題の難易度が上昇するにもかかわらず、推論労力を削減し始めます。この現象はo3-miniバリアントで最も顕著で、Claude-3.7-Sonnet(思考)モデルではそれほど顕著ではありません。特に、十分な推論予算を利用できる状態で世代長の制限をはるかに下回る動作をしているにもかかわらず、これらのモデルは問題が複雑になるにつれて思考フェーズで追加の推論計算を活用できていません。この動作は、問題の複雑さに対する現在の推論モデルの思考能力の根本的なスケーリング限界を示唆しています。
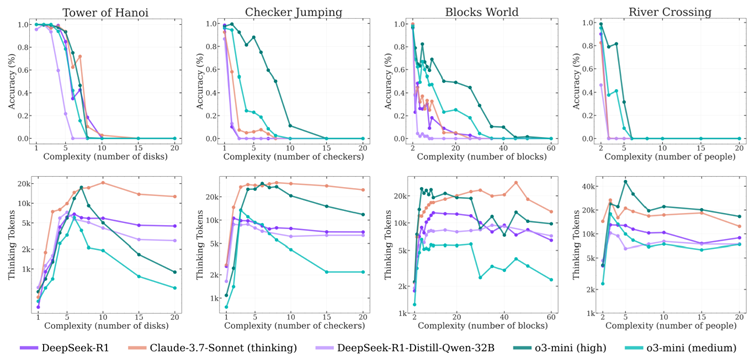
図6:パズル環境における推論モデルの精度と思考トークン数と問題の複雑さの関係。複雑さが増すにつれて、推論モデルは当初より多くのトークンを消費しますが、精度は徐々に低下し、ある臨界点に達すると推論は破綻します。つまり、パフォーマンスが急激に低下し、推論にかかる労力も減少します。
推論モデルの思考プロセスに関するより深い洞察を得るために、推論トレースの詳細な分析を実施しました。図1に示すように、パズル環境を用いた設定により、最終的な答えだけでなく、これらのモデルが生成する推論トレース(「思考」)に関するより詳細な洞察を得ることができます。パズルシミュレータを用いて、モデルの思考の中で探求された中間解を抽出し、分析します。この調査では、これらの中間解のパターンと特性、推論プロセスにおける順序位置に対する正確性、そして問題の複雑さの増加に伴ってこれらのパターンがどのように変化するかを検証します。この分析では、パズルスイート全体にわたってClaude-3.7-Sonnet-Thinkingによって生成された推論トレースに焦点を当てます。トレース内で特定された各中間解について、(1)推論トレース内の相対位置(総思考長で正規化)、(2)パズルシミュレータによって検証された正確性、(3)対応する問題の複雑さを記録しました。これにより、推論プロセス全体を通じてソリューション開発の進行と精度を特徴付けることができます。
図7aは、思考における中間解の位置、その正しさ、そしてあらゆるパズル環境における問題の複雑さの関係を示しています。推論トレースからの分析は、上記で議論した3つの複雑さの領域をさらに検証するものです。より単純な問題の場合、推論モデルは思考の初期段階で正しい解を見つけることが多いものの、その後は誤った解の探索を続けます。誤った解(赤)の分布は、正しい解(緑)と比較して、思考の終わりに向かってより上方にシフトしていることに注意してください。文献では「考えすぎ」と呼ばれるこの現象は、計算の無駄につながります。問題が中程度に複雑になると、この傾向は逆転します。モデルは最初に誤った解を探索し、その後、主に思考の後半で正しい解に到達します。今回は、誤った解(赤)の分布は、正しい解(緑)と比較してより下方にシフトしています。最後に、より複雑な問題では、モデルが思考の中で正しい解を生成できないことを意味する崩壊が発生します。
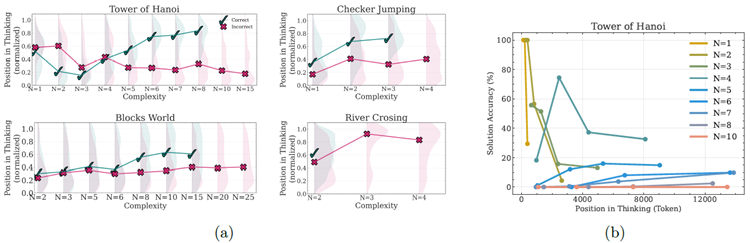
図7:左と中央:4つのパズルにおける推論の軌跡における中間解の位置と正確性。✓は正解、✗は不正解を示し、分布密度は網掛けで示されています。右:ハノイの塔における、異なる複雑さにおける思考過程における解答の正確性と解答位置の関係。単純な問題(\(N=1-3\))では、時間の経過とともに早期の正確性が低下し(考えすぎ)、中程度の問題(\(N=4-7\))では推論を続けることで正確性がわずかに向上し、複雑な問題(\(N ≥8\))では一貫して正確性がほぼゼロであり、推論が完全に失敗したことを示しています。
このセクションでは、正確な問題解決手順を実行する際の推論モデルの限界に関する驚くべき結果を示し、また、移動回数に基づいたモデルの異なる動作を示します。
図 8a と 8b に示すように、ハノイの塔の環境では、プロンプトでアルゴリズムを提供してモデルが規定の手順を実行するだけで済むようにした場合でも、パフォーマンスは向上せず、観測された崩壊はほぼ同じ時点で依然として発生します。解決策を見つけて考案するには、単に特定のアルゴリズムを実行するよりも、はるかに多くの計算 (検索と検証など) が必要になるはずなので、これは注目に値します。これは、検証と問題を解決するための論理的手順に従うことにおける推論モデルの限界をさらに強調しており、このようなモデルの記号操作機能を理解するにはさらなる研究が必要であることを示唆しています [44 , 6]。さらに、図 8c と 8d では、クロード 3.7 ソネットの思考モデルとは非常に異なる動作が見られます。ハノイの塔環境では、提案された解におけるモデルの最初のエラーは、多くの場合、(\(N=10\)) の場合 100 手目あたりなど、かなり後の段階で発生します。これに対し、川を渡る環境では、モデルは 4 手目まで有効な解を生成できません。また、このモデルは、31 手を必要とする (N=5\) のハノイの塔を解く際にはほぼ完璧な精度を達成しますが、11 手で解ける (\(N=3\)) の川を渡るパズルを解くことができないことに注意してください。これは、Web 上で \(N >2\) の川を渡る例がほとんどないことを示唆しており、LRM はトレーニング中にこのような例に頻繁に遭遇したり、記憶したりしなかった可能性があります。
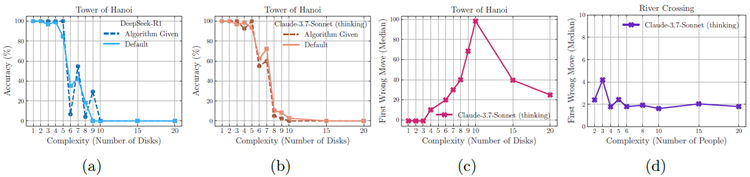
図 8: (a) および (b) プロンプトでソリューション アルゴリズムを提供しているにもかかわらず、同様のポイントで実行エラーが発生し、論理ステップ実行における推論モデルの限界が強調されています。 (c) および (d) 特に、Claude 3.7 Sonnet モデルは、川を渡るシナリオの初期のエラーと比較して、ハノイの塔でエラーのないシーケンスがはるかに長くなっています。
本稿では、制御可能なパズル環境を用いて、問題の複雑性という観点から、最先端の大規模推論モデル(LRM)を体系的に検証する。その結果、現行モデルには根本的な限界があることが明らかになった。高度な自己反省メカニズムを備えているにもかかわらず、これらのモデルは特定の複雑性閾値を超えると、一般化可能な推論能力を開発できない。我々は3つの異なる推論領域を特定した。標準的なLLMは低複雑性ではLRMよりも優れた性能を示し、LRMは中複雑性で優れた性能を示し、高複雑性では両者とも限界に達する。特に懸念されるのは、問題が臨界複雑性に近づくにつれて推論労力が直感に反して減少することであり、これはLRMの計算スケールの本質的な限界を示唆している。推論トレースの詳細な分析により、単純な問題における非効率的な「考えすぎ」から複雑な問題における完全な失敗に至るまで、複雑性に依存する推論パターンがさらに明らかになった。これらの知見は、LRMの能力に関する一般的な仮定に疑問を投げかけ、現行のアプローチが一般化可能な推論への根本的な障壁に直面している可能性を示唆する。最後に、LRMに関するいくつかの驚くべき結果を示し、今後の研究に向けたいくつかの未解決の課題を提示した。最も注目すべき点は、正確な計算を行う際の限界が観察されたことです。例えば、「ハノイの塔」の解アルゴリズムをモデルに提供した場合でも、このパズルにおけるパフォーマンスは向上しませんでした。さらに、モデルの最初の失敗手を調べると、驚くべき挙動が明らかになりました。例えば、「ハノイの塔」では最大100手正解できたのに対し、「川渡り」パズルでは5手以上正解できなかったのです。この結果は、これらのシステムの推論能力に関する今後の研究への道を開くものと考えています。
本研究には限界があることを認識しています。本研究のパズル環境は、問題の複雑さをきめ細かく制御しながら制御された実験を可能にしますが、推論タスクのごく一部しか表しておらず、現実世界や知識集約型の推論問題の多様性を捉えきれていない可能性があります。注目すべきは、本研究の実験のほとんどが、閉境LRMへのブラックボックスAPIアクセスに依存しているため、内部状態やアーキテクチャコンポーネントの分析能力が制限されていることです。さらに、決定論的なパズルシミュレータの使用は、推論が段階的に完全に検証できることを前提としています。しかし、構造化されていない領域では、このような正確な検証は実現不可能な場合があり、この分析をより一般化可能な他の推論手法に転用できる可能性が制限されます。
著者は、貴重なフィードバックとサポートを提供してくれた Scott Hoang、Yichen Jiang、Minsik Cho、Mohammad Sekhavat、David Harrison、Mohammadreza Armandpour、および Devi Krishna に感謝の意を表します。
この付録では、実験セットアップの仕様、追加の結果、拡張分析など、本文を補足する詳細を提供します。
問題の説明 ハノイの塔は古典的な再帰パズルで、推論モデルの順次推論および計画能力を評価するための優れた問題となります。このパズルは 3 つの杭 (左から右に 0、1、2 とラベル付け) とさまざまなサイズの N 枚のディスクで構成され、各ディスクには 1 (最小) から N (最大) までの一意の番号が付けられています。初期構成では、N 枚のディスクすべてがサイズの降順で左端の杭 (杭 0) に積み重ねられ、最大のディスクが一番下、最小のディスクが一番上になります。残りの 2 つの杭 (1 と 2) は最初は空です。目標は、同じサイズの順序 (最大が一番下、最小が一番上) を維持しながら、すべてのディスクを杭 0 から杭 2 に移動することです。このパズルは、3 つの基本的な制約によって決まります。(1) 単一のディスクの移動: 一度に移動できるディスクは 1 枚だけです。 (2) 最上部のディスクアクセス:どの杭からでも最上部のディスクのみを移動対象として選択できます。(3) サイズ順序制約:大きいディスクを小さいディスクの上に置くことはできません。このパズルは、問題をサブ問題に分解する(再帰的思考)、複数の状態とディスクの位置を同時に追跡する(ワーキングメモリ管理)、移動ルールと制約を遵守しながら事前に計画を立てる(制約充足)、最終目標を達成するための正しい操作順序を決定する(順次計画)といった重要な認知的要求をモデルに示す必要があるため、モデルの推論能力と計画能力を評価するための優れたテストベッドとなります。
\(N\) 枚のディスクを用いたハノイの塔再帰パズルを解くために必要な最小移動回数は \(2N −1\) であり、指数関数的にスケーリングする問題となります。この特性により、初期ディスク数に応じて問題サイズを調整することで、きめ細かな難易度制御が可能になります。しかし、本評価フレームワークでは、最適性ではなく解の正しさに重点を置き、各移動の妥当性とモデルが目標状態に到達する能力を成功基準として評価します。
プロンプトのデザイン システムプロンプトは、パズルのセットアップを説明した明確な問題文から始まります。動きのルールと、すべてのディスクを3番目の杭に移動させるという目的が明確に示されています。理解を容易にするために、プロンプトには例題のデモンストレーションに加え、重要なフォーマットと推論の期待値が含まれています。
システムプロンプト - ハノイの塔
あなたは親切なアシスタントです。このパズルを解いてください。
3つの杭があり、最初の杭に n 枚の異なるサイズのディスクが積み重ねられています。ディスクには1(最小)からn(最大)までの番号が付けられています。このパズルにおけるディスクの動きは以下のとおりです。
1. 一度に動かせるディスクは1枚だけです。
2. 各動きは、1つの積み重ねから一番上のディスクを取り、別の積み重ねの上に置くことで構成されます。
3. 大きいディスクを小さいディスクの上に置くことはできません。
目標は、積み重ねられたディスク全体を3番目の杭に移動させることです。
例:1(最小)、2、3(最大)の番号が付けられた3枚のディスクがある場合、初期状態は[[3, 2, 1]、[]、[]]で、解は次のようになります。
moves = [[1 , 0, 2]、[2, 0, 1]、[1, 2, 1]、[3, 0, 2]、
[1, 1, 0]、[2, 1, 2]、[1, 0, 2]]
これは、ディスク1を杭0から杭2に移動し、次にディスク2を杭0から杭1に移動し、というように繰り返すことを意味します。
要件:
• 思考プロセスで潜在的な解決策を検討する際は、常に対応する移動の完全なリストを含めてください。
• 位置は0からインデックス付けされます(左端の杭が0です)。
• 最終的な回答には、移動の完全なリストを次の形式で含めてください: moves = [[ディスクID, 移動元杭, 移動先杭], ...]
システム プロンプトの後のユーザー プロンプトには、杭間のディスクの分布を示す現在の構成と、ターゲット状態を指定する目標構成を含む特定のパズル インスタンスが表示されます。
ユーザープロンプト N 枚のディスク用テンプレート -ハノイの塔
異なるサイズのディスク N 枚のパズルがあります。
初期設定:
• 杭 0: N (下)、... 2、1 (上)
• 杭 1: (空)
• 杭 2: (空)
ゴール設定:
• 杭 0: (空)
• 杭 1: (空)
• 杭 2: N (下)、... 2、1 (上)
ルール:
• 一度に動かせるディスクは 1 枚だけです。
• どのスタックでも、一番上のディスクだけを移動できます。
• 大きいディスクを小さいディスクの上に置くことはできません。
初期配置を目標配置に変換するための移動順序を見つけてください。
シミュレータ:LRMから得られる解の厳密かつ一貫した評価を保証するため、各パズルに個別のパズルシミュレータを採用しています。ハノイの塔シミュレータは、3つの杭間のディスク構成を追跡し、提案された各移動をパズルの基本制約に照らして検証する、ステートフルな環境として設計されています。シミュレータのアーキテクチャは、状態管理、移動の検証、解の検証を明確に分離したモジュール型設計パターンに従っています。このシミュレータには、現在のディスク構成を追跡し、パズルの基本制約を適用するパズルクラスがあります。また、パズルのセットアップにおける各移動を実行し、4層の検証を行うメソッドも用意されています。4層の検証とは、杭境界条件(0~2)のチェック、元の杭にディスクが含まれていることの検証、指定されたディスクが最上位にあることの確認、そして大きなディスクが小さなディスクの上に配置されないようにするサイズ順序制約の適用です。検証が成功すると、メソッドはディスク転送を実行し、ゲームの状態を更新します。次に、移動リストを順番に処理し、目標状態の達成を確認することで、完全なソリューションの検証が行われます。
問題の説明 チェッカージャンピングは、1次元の制約充足パズルで、連続的な推論、計画、ルール理解能力をテストするように設計されています。このパズルは、赤いチェッカー(’R’)、青いチェッカー(’B’)、そして1つの空きスペース(’_’)が直線状に並んだものです。標準的な配置では、N個の赤いチェッカーが左側に配置され、その後ろに中央に空きスペース、そして右側にN個の青いチェッカーが配置され、長さ \(2N + 1\) の直線状のボードが形成されます。目的は、すべての赤と青のチェッカーの位置を入れ替え、最初の配置を実質的に反転させることです。つまり、赤いチェッカーが右側、青いチェッカーが左側に配置されます。このパズルにおける動きは、2つの基本ルールに従います。(1) スライド移動:チェッカーは隣接する空きスペースに前方にスライドすることができます。(2) ジャンプ移動:チェッカーは、反対色のチェッカーを1つだけ飛び越えて空きスペースに着地することができます。したがって、チェッカーはスタート地点から後退することはできません。つまり、赤チェッカーは右方向、青チェッカーは左方向のみに移動できます。このパズルは認知的な課題を提示するため、推論モデルの優れたテストベッドとなります。例えば、モデルは空間推論(チェッカーの位置と可能な動きを追跡する)、制約充足(パズル中の移動ルールの遵守)、先読み計画(現在の動きがゴールへの将来の可能性にどのように影響するかを予測する)、状態空間探索(可能な動きのシーケンスを検索して有効な解を見つける)のいずれかの側面を示す必要があります。
チェッカージャンピングパズルの難易度はチェッカーの数に比例します。各色のチェッカーがN個の場合、最小解は \((N + 1)^2−1\) 回の移動を必要とし、問題の大きさと解の複雑さの間には二次関係が生まれます。私たちの評価フレームワークでは、最適性よりも解の正しさに主に焦点を当て、各移動をパズルの制約に照らし合わせて評価し、最終状態が目標構成と一致することを確認します。このアプローチにより、解の過程で発生する可能性のある推論の失敗や制約違反を正確に特定できます。
プロンプトのデザイン システムプロンプトは、パズルの設定と動きのルールを説明した明確な問題文から始まります。目的を明確に示し、小さなボード構成を用いた具体的な例を用いて、動きの表現方法を説明します。
システムプロンプト-チェッカージャンプ
あなたは親切なアシスタントです。このパズルを解いてください。
1次元のボード上に、赤いチェッカー (’R’)、青いチェッカー (’B’)、そして1つの空きスペース (’_’) があります。チェッカーは次のいずれかの方法で移動できます。
1. 隣接する空きスペースに前方にスライドする。または
2. 反対色のチェッカーを1つだけ飛び越えて空きスペースに着地する。
目標は、すべての赤と青のチェッカーの位置を入れ替え、初期状態を反転させることです。
例: 初期状態が [’R’, ’_’, ’B’] の場合、目標は [’B’, ’_’, ’R’] に到達することです。解答は、各移動が [チェッカーの色、位置の開始位置、位置の終了位置] で表される移動のリストである必要があります。例:
moves = [[’R’, 0, 1], [’B’, 2, 0], [’R’, 1, 2]]
これは、赤いチェッカーを位置0から1に移動し、次に青いチェッカーを位置2から0に移動し、というように繰り返すことを意味します。
要件:
• 思考プロセスで潜在的な解決策を検討する際は、常に対応する移動の完全なリストを含めてください。
• 位置は0からインデックス付けされます(左端の位置が0です)。
• 最終的な答えには、最終解決策の移動の完全なリストが moves = [[checker_color, position_from, position_to], ...] という形式で含まれていることを確認してください。
ユーザー プロンプトには、初期のボード構成と目標状態を含む特定のパズル インスタンスが表示されます。
ユーザープロンプト N 個のチェッカーチェッカージャンプ用のテンプレート
2N+1 個の位置を持つパズルがあります。左側に N 個の赤いチェッカー (’R’)、右側に $N$ 個の青いチェッカー (’B’)、そしてその間に 1 つの空きスペース (’_’) が一列に並んでいます。
初期ボード: R R ... R _ B B ... B
ゴールボード: B B ... B _ R R ... R
ルール:
• チェッカーは隣接する空きスペースに滑り込むことができます。
• チェッカーは反対色のチェッカーを 1 つだけ飛び越えて空きスペースに着地することができます。
• チェッカーは後方 (スタート側) に移動することはできません。
初期ボードをゴールボードに変換するための最小の動きの順序を求めてください。
シミュレータ: 評価フレームワークでは、チェッカージャンピングパズルの解を検証するためにカスタムシミュレータを採用しています。このシミュレータは、パズルのすべての制約を適用しながら、解のパス全体にわたって状態の推移を追跡する包括的な検証システムを実装しています。チェッカージャンピングシミュレータは、すべてのチェッカーと空きスペースの位置を追跡し、パズルの移動ルールに照らし合わせて、与えられた解の各移動を検証する、ステートフルな環境として設計されています。シミュレータはまず、初期状態とゴール状態の両方が、赤と青のチェッカーが同じ数で、空きスペースが 1 つだけ含まれている、整形式であることを検証します。次に、各移動は、位置の境界の検証、ソースでのチェッカーの色の正確さの確認、ターゲット位置が空であることの確認、移動タイプがスライド(距離 = 1)またはジャンプ(距離 = 2)であることを検証する、多層検証を実行するメソッドを使用して実行されます。シミュレータは、後方への移動を阻止する方向制約(赤いチェッカーは右へ、青いチェッカーは左へ)を適用し、ジャンプ動作の検証は、中央の位置に反対色のチェッカーが存在することを確認することで行います。検証に成功すると、位置を更新し、ソースをクリアすることでチェッカーの移動を実行します。その後、最終的な目標状態を検証しながら、動作シーケンス全体を処理します。
問題の説明 川渡りは、マルチエージェントの調整と制約管理をテストする制約満足度計画パズルです。 このパズルは、宣教師と人食い人種問題や橋とたいまつ問題など、計画に関する文献 [45 , 46] で広く研究されてきた古典的な問題を一般化したものです。 川渡りパズルには、N 人のアクター (\(a_1, a_2, ..., a_N\) で示される) とそれに対応する \(N\) 人のエージェント (\(A_1, A_2, ..., A_N\) で示される) が関与し、ボートを使用して川を渡らなければなりません。 初期状態では、すべての \(2N\) 人が川の左岸にいます。 目標は、全員を安全に右岸まで輸送することです。このパズルは、いくつかの重要な移動制約の下で動作します。(1) ボートの定員制約: ボートは一度に最大 k 人の個人を運ぶことができます。k は通常、小さいパズル (\(N ≤ 3\)) の場合は 2、大きいパズル (\(N ≤ 5\)) の場合は 3 に設定されます。(2) ボートが空でない制約: ボートは空で移動することはできず、少なくとも 1 人が乗っている必要があります。(3) 安全制約: エージェントは競合するエージェントからクライアントを保護する必要があるため、アクターは自分のエージェントも存在しない限り、他のエージェントの存在下にいることはできません。この安全制約は、岸とボートの両方に適用されます。このパズルでは、参加者が常に安全制約を維持しながら慎重に横断を調整する必要があるため、複雑な計画と状態追跡が必要です。解答者は、安全に一緒に移動できる個人のさまざまな組み合わせを推論し、横断後に誰がボートで戻るべきかを決定し、最終的に制約に違反することなく全員を右岸に連れて行くシーケンスを戦略的に計画する必要があります。このタスクの複雑さは、アクターとエージェントのペアの数とボートの容量を調整することで制御でき、推論モデルにスケーラブルな課題を生み出します。
プロンプトの設計。 システムプロンプトは、アクターとエージェントを表す表記法を導入し、ボートの動きのリストとしてソリューション形式を確立し、その形式を示す簡単な例を提供します。
システムプロンプト- 川渡り
あなたは親切なアシスタントです。このパズルを解いてください。
アクターは a1、a2、…、エージェントは A1、A2、… で表すことができます。解答はボートの移動のリストでなければなりません。各移動はボートに乗っている人々を表します。例えば、アクターが2人、エージェントが2人いる場合、次の式を返す必要があります。
moves =[[" A_2", "a_2 "], [" A_2 "], [" A_1", "A_2 "], [" A_1 "], [" A_1", "a_1
"]]
これは、最初の移動では A_2 と a_2 が左から右へ並び、2番目の移動では A_2 が右から左へ並び、以下同様に続くことを示します。
要件:
• 思考プロセスにおいて潜在的な解決策を検討する際は、必ず対応するボートの動きの完全なリストを含めてください。
• リストにはコメントを含めないでください。
• 最終的な回答にも、最終的な解決策に必要な動きの完全なリストが含まれていることを確認してください。
ユーザープロンプトには、N 個のアクターとエージェントのペア、ボートの定員 k、およびソリューション全体で維持する必要がある安全制約を含む特定のパズルインスタンスが表示されます。
シミュレータ: 評価フレームワークでは、川渡りパズルから抽出された解を検証するためにカスタム シミュレータを採用しています。シミュレータは、すべてのパズル制約を適用しながら、すべての個体 (アクターとエージェント) の状態とボートの位置を追跡します。各移動は、ボートの定員制限の確認、すべての乗客がボートの現在の側にいるかどうかの確認、および移動後のボート上と各岸の両方で、アクターが自分のエージェントがいない限り他のエージェントの存在下にいられないという重要な安全制約の適用など、複数段階の検証を伴って実行されます。シミュレータは、動的なボートの位置を管理し、各横断後に自動的に側を切り替え、各移動後に完全な状態を検証して、どちらの岸でも安全違反が発生しないことを確認します。次に、完全な横断シーケンスが検証され、2 N 個の個体すべてが右岸に正常に到達します。
問題の説明 Blocks Worldは、LLMの計画能力を分析するために最近研究されている古典的なプランニングパズルです[37, 38]。このパズルは、複数のブロック(A、B、Cなど)のスタックを、初期構成から指定された目標構成に再配置するものです。各ブロックは文字によって一意に識別され、初期状態を目標状態に変換するために必要な最小限の移動シーケンスを見つけることが目的です。このパズルは、2つの基本的な制約の下でのみ動作します。(1) 最上位ブロックの移動:スタックの最上位ブロックのみを移動できます。(2) 有効な配置:ブロックは、空いている位置か、他のブロックの上にのみ配置できます。これらの制約により、操作の順序が重要になるプランニング問題が生じます。これは、一部の構成では、後で下にあるブロックにアクセスするために、一時的にブロックを配置する必要がある場合があるためです。Blocks Worldは、前向きな思考と状態追跡を必要とするため、推論モデルのプランニング能力を評価するための優れたテストベッドとして機能します。最近の研究では、このパズルを様々な設定で検証し、3~5ブロックという簡略化された設定を含む、シーケンシャルプランニングタスクにおけるLLMのパフォーマンスを評価しています[37, 38]。モデルは、複雑な状態遷移を有効なシーケンシャルムーブメントに分解し、ブロック間の依存関係を推論し(例えば、下位のブロックにアクセスする前にブロックを解除する)、不正なムーブメントを伴わずに目標状態へのパスを効率的に計画する能力を示す必要があります。
このパズルの難易度は、ブロック数、スタック数、そして初期構成と目標構成の複雑さといったいくつかのパラメータを調整することで調整できます。複雑性は主にブロック数Nによって制御しますが、初期構成と目標構成には明確な構造パターンが存在します。実験設計では、初期構成ではN個のブロックがアルファベット順に2つのスタックに分割され、3つ目のスタックは作業スペースとして空けられます。目標構成では、すべてのブロックが最初のスタックに統合され、2つの初期スタックのブロックが交互に配置されます。この配置は、既存のスタックを完全に分解して再構成する必要がある特定の配置です。例えば、N = 4の場合、初期状態ではブロックが2つのスタック[["A", "B"], ["C", "D"], []]に分割され、目標状態[["D", "B", "C", "A"], [], []]では両方のスタックのブロックが交互に配置されます。また、 N = 6 の場合、初期状態 [["A", "B", "C"], ["D", "E", "F"], []] を [["F", "C", "E", "B", "D", "A"], [], []] に変換して、複雑な交互パターンを形成する必要があります。 N が増加すると、状態空間は階乗的に大きくなり、最小解の長さは N とともにほぼ線形に増加します。 N の値が小さい場合 (2-7)、パズルは基本的な計画をテストします。中程度の値の場合 (8-20)、より長い計画期間を伴うより複雑な推論が必要になり、値が大きい場合 ( N > 20 )、長い解決パス全体で広範な一時的な動きとパターン認識が必要になることで、順次推論機能の限界に挑戦します。
プロンプトのデザイン。 システム プロンプトは、Blocks World パズルの基本的なルールを紹介し、移動の表現形式を確立し、解決構造を示す簡単な例を提供します。
システムプロンプト - Blocks World
あなたは親切なアシスタントです。このパズルを解いてください。
このパズルでは、ブロックが積み重ねられており、一連の動きを使って、目標の構成にブロックを並べ替えることが目的です。
• どの積み重ねでも、一番上のブロックだけを動かすことができます。
• ブロックは、空いている位置に置くことも、他のブロックの上に置くこともできます。
例:初期状態が ["C"]] の場合、解決策は次のようになります。
[["A", "B"], ["C"], []]
そして目標状態は
[["A"], ["B"],
moves = [["C", 1, 2], ["B", 0, 1]]
これは、ブロック C をスタック 1 からスタック 2 に移動し、次にブロック B をスタック 0 からスタック 1 に移動させることを意味します。
要件:
• 思考プロセスにおいて潜在的な解決策を検討する際は、必ず対応する移動の完全なリストを含めてください。
• 最終的な答えにも、最終解決策の移動の完全なリストが、moves = [[ブロック, from stack, to stack], ...] という形式で含まれていることを確認してください。
ユーザープロンプトは、提供された初期構成と目標構成を含む特定のパズルインスタンスを提示し、モデルに移動制約を明示的に通知します。
N 個のブロック用ユーザープロンプトテンプレート - BlocksWorld
N 個のブロックを使ったパズルがあります。初期状態:
スタック 0: blocks_0 (上)
スタック 1: blocks_1 (上)
…
スタック m: blocks_m (上)
ゴール状態:
スタック 0: goal_blocks_0 (上)
スタック 1: goal_blocks_1 (上)
…
スタック m: goal_blocks_m (上)
初期状態を目標状態に変換するための最小の移動シーケンスを見つけてください。各スタックの最上部のブロックのみを移動できることを覚えておいてください。
シミュレータ。当社の評価フレームワークは、Blocks Worldパズルから抽出された解を検証するためにカスタムシミュレータを採用しています。シミュレータは、パズルの移動制約を適用しながら、スタック全体のすべてのブロックの状態を管理します。各移動は、パズルのセットアップ内で3層の検証を経て実行されます。検証は、スタックインデックスが境界内にあること、ソーススタックにブロックが含まれていること、指定されたブロックがスタックの先頭にあること(最上位ブロックのみの移動ルールを適用)の3層です。検証が成功すると、ブロック転送が実行され、ブロックはソーススタックからポップされ、宛先スタックに追加されます。最後に、ブロック移動の完全なソリューションシーケンスが処理され、結果の構成が目標のゴール状態と一致することが検証されます。
構成 私たちの実験では、思考プロセスを徹底的に分析できるように、主に推論モデルとその非思考モデルを使用しました。分析に不可欠な思考トレースにアクセスできるため、Claude 3.7 Sonnet(思考/非思考)とDeepSeek-R1 / V3を特に選択しました。最終的な精度メトリックのみに焦点を当てた実験では、思考にアクセスできないため、OpenAIのo3-miniモデルの結果も含めました。Claude 3.7 Sonnet(思考および非思考)モデルでは、APIインターフェイスを介してアクセスする最大64,000トークンの生成予算を使用しました。すべてのAPI rus(Claude-3.7-Sonnetおよびo3-mini実行)の温度は1.0に設定されています。 DeepSeek-R1、DeepSeek-V3、DeepSeek-R1-Distill-Qern-32Bを用いた実験は、ローカルサーバー上で実施され、最大世代長は64,000、温度は1.0に設定されています。すべての実験において、各複雑度レベル(N値)でパズルインスタンスごとに25個のサンプルを生成し、全サンプルの平均パフォーマンスを報告しました。
解決策の抽出 モデルの応答と中間推論トレース(思考)を処理するためのカスタム抽出パイプラインを開発しました。このパイプラインは複数の主要コンポーネントで構成されています。最終的な応答と思考トレースの両方において、潜在的な解決策の試みを特定するために、柔軟な正規表現ベースの抽出器を実装しました。抽出プロセスでは、正規表現を用いて解決策のパターン(明示的な「 moves = 」パターンと代替的な括弧ベースの解決策の両方)を特定します。抽出された候補解決策は、(i) リストからコメント(任意の行の「#」に続くテキスト)を削除し、(ii) 文脈から示唆される動きの形式に正規化することで、一貫性のある構造を確保することで、処理およびクリーンアップされます。次に、解決策の形式と構造を検証し、無効な一致を除外します。抽出中に、抽出された各解決策のトークン位置のメタデータも取得します。特に、思考トレース内の位置を正確に追跡するために、対応するモデルと同じトークナイザー(cl100k_base)を使用して、すべての実験でトークンをカウントしました。また、サンプル間の比較を可能にするために、トークンの位置は思考の長さに対して正規化されました。最後に、思考トレース内に記録された解が一意であることを確認し、重複する解(同一の手のリスト)は除外します。重複する解がある場合は、最初の解のみが分析のために記録されます。
解の評価 抽出後、各解候補は詳細な検証のために対応するパズルシミュレータに渡されます。シミュレータは解を移動リストとして受け取り、パズルに対して評価します(各パズルシミュレータの詳細については付録A.1を参照してください)。合成解の各移動は、以前の移動とパズルのルールに従って順番に実行されます。次に、シーケンス内のすべての移動から得られた最終状態がパズルの目標状態と比較され、完全な解の正しさが判定されます。誤った解については、パズルシミュレータによる移動検証中に、最初の失敗した移動の詳細と失敗の種類も収集されます。
規定ステップの実行 さまざまなパズルにわたるオープンエンドの問題解決に加えて、規定ステップによる明示的な解決アルゴリズムのガイダンスを提供することがこれらの推論モデルの動作にどのように影響するかをテストするための集中的な実験も実施しました(セクション4.4)。ゼロから解決策を見つけて考案するには、特定のアルゴリズムの手順に従うだけよりも、モデルに対してかなり多くの計算(検索と検証など)が必要になると予想しました。ただし、図8aと8bの結果は、推論モデルの動作はそれほど変わらず、この設定では以前とほぼ同じポイントで崩壊が発生することを示しています。この発見は、制限が問題解決と解決策戦略の発見だけでなく、生成された推論チェーン全体にわたる一貫した論理的検証とステップ実行の制限にも存在するという証拠を強化します。
例えば、モデルにはハノイの塔パズルを解くための完全な再帰アルゴリズムが以下のように提供されています。このアルゴリズムのスクラッチパッドは、推論行動への影響をテストするために、標準的な問題プロンプトに追加されました。
ハノイの塔の規定アルゴリズムの例
パズルを解くための再帰アルゴリズムの擬似コードを以下に示します。
アルゴリズム Solve(n, source, target,auxiliary, moves)
// n = 移動するディスクの枚数
// source = 開始杭 (0, 1, または 2)
// target = 移動先杭 (0, 1, または 2)
//auxiliary = 未使用の杭 (0, 1, または 2)
// moves = 移動のシーケンスを格納するリスト
IF n = 1 THEN
// ソース杭の一番上のディスクを取得
disk = ソース杭の一番上のディスク
// 移動をリストに追加: [disk_id, source, target]
ADD [disk, source, target] to moves
RETURN
END IF
// n-1 個のディスクをソースから補助杭に移動する Solve(n-1, ソース, 補助, ターゲット, moves)
// n 番目のディスクをソースからターゲットに移動する ディスク = ソース杭の一番上のディスク ADD [disk, source, target] to moves
// n-1 個のディスクを補助からターゲットに移動する
Solve(n-1, 補助, ターゲット, ソース, moves) END ALGORITHM
n枚のディスクを杭0から杭2へ移動するパズル全体を解くには、次のようにします。
1. 空のリスト「moves」を初期化します。
2. Solve(n, 0, 2, 1, moves) を実行します。
3. 「moves」リストに完全な解が格納されます。
注: この擬似コードを実行する際は、各杭の上にあるディスクを追跡してください。「moves」リスト内のディスクIDは、実際に移動するディスクに対応している必要があります。
このアルゴリズムは、問題を段階的に解くためのスクラッチパッドとして使用できます。
構成深度とは、完全な解に到達するまでに必要な連続した操作(つまり、移動)の数です。図9は、4つのパズル環境において、この深度が問題のサイズ(N)に応じてどのように変化するかを示しています。各パズルには、その基礎となる計算複雑性を反映した明確な成長パターンがあります。例えば、「ハノイの塔」は指数関数的な成長(\(2N−1\))を示し、「チェッカージャンピング」は二次関数的な成長(\((N + 1)^2 − 1\))を示します。「川渡り」パズルと「ブロックワールド」パズルは、Nに対してより緩やかで、ほぼ線形な成長を示します。これらの変化する構成深度プロファイルにより、言語推論モデルがさまざまな種類の連続推論課題をどのように処理するか、また、その精度がパズルを解くために必要な構成深度と常に相関しているかどうかを評価できます。この分析の詳細は、付録A.4の図10に記載されています。
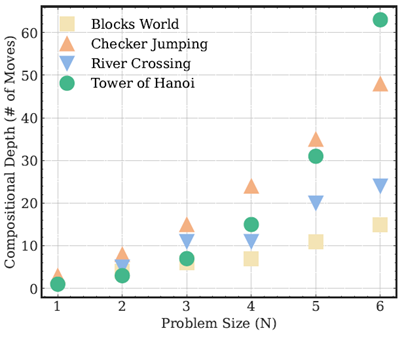
図 9: 4 つのパズル環境におけるさまざまな問題サイズの構成の深さ (必要な移動回数)。
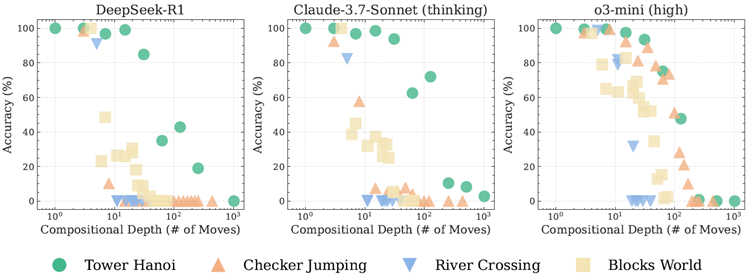
図 10: 4 つのパズル環境における 3 つの LRM (DeepSeek-R1、思考機能付き Claude-3.7-Sonnet、o3-mini) の精度と構成の深さ (必要な移動回数) の関係。
直感的には問題の複雑さとモデルの精度の間には負の相関関係があると思われますが、私たちの分析では、構成の深さと LRM のパフォーマンスの間にはより微妙な関係があることが明らかになりました。図 10 は、私たちのパズル スイートにおける 3 つの最先端推論モデル (Claude-3.7-Sonnet w. thinking、DeepSeek-R1、o3-mini) 全体でこれを示しています。個々のパズルの種類内では、予想される負の相関関係が見られます。つまり、構成の深さが増すにつれて、モデルの精度は一貫して低下します。ただし、異なるパズルの種類間では、この関係は崩れます。モデルは、構成の深さの低いパズルでは苦戦する一方で、構成の深さが高い別のパズルでは成功する場合があります。たとえば、モデルは、約 \(10^2\) の移動を必要とするハノイの塔のインスタンスで 50% を超える精度を達成しますが、構成の深さが大幅に低い (\(∼10^1\) の移動)
失敗分析 モデルが構成的推論ステップのどこで失敗するかを理解することで、2元的な成功指標を超えた洞察が得られます。精度評価には、手順全体を完璧に実行することが必要であり、1つの誤った動きでも失敗に終わります。失敗パターンをより詳細に調査するために、モデルが最初に誤った動きをする構成の深さを、問題の複雑さのレベルに応じて分析します。
図11は、解法シーケンスにおける失敗手IDと問題の複雑さ(\(N\))の関係を示しています。上段は思考機能ありとなしのClaude-3.7-Sonnetを比較し、下段はDeepSeek-R1(思考あり)とDeepSeek-V3(非思考あり)を比較しています。これらの比較は、LRMの思考メカニズムがパズルの合成推論タスクにおける失敗パターンにどのように影響するかを示しています。分析から、直感に反するパターンがいくつか浮かび上がりました。まず、モデルは問題の複雑さに対して非単調な失敗挙動を示します。つまり、全体的な解法が長くなるにもかかわらず、N値が高いほどモデルが解法シーケンスの早い段階で失敗する例です。例えば、ハノイの塔では、モデルは\(N = 15\)では50手未満で失敗することがありますが、\(N = 8\)では100手以上で成功することがあります。これは、同じパズルに対する効果的なアルゴリズムの計画と実行は、解法の進行に対して一貫した失敗パターンを維持するという期待と矛盾しています。これは、モデル(LRMとそれらの非思考型標準LLMの両方)が学習した解法戦略を異なる問題スケールに適用する方法に根本的な矛盾があることを示唆しています。また、両方のモデルバリアントが完全に精度を崩壊させる高複雑度領域(例えば、\(N ≥ 15\)のハノイの塔と\(N ≥ 40\)のブロックワールド)では、非思考型モデルは時折、解法シーケンスのより深い段階までパフォーマンスを維持し、思考型バリアントよりも後の手で失敗する可能性があることが観察されています。これは、LLMにおける構成的推論の失敗が単にコンテキスト長や推論計算の不足によるものではなく、モデルが問題スケール全体でアルゴリズムの一貫性を維持する方法における根本的な限界を反映していることを示しており、興味深いものです。また、モデル推論の一貫性と信頼性を理解するために、失敗手の位置の分布特性も分析します。図12は、各パズル環境のすべての問題複雑度にわたって集計された失敗手の位置の密度分布を示しており、同じファミリー内の思考型モデルと非思考型モデルを比較しています。図を見ると、思考モデル(思考機能付きClaude-3.7-SonnetとDeepSeek-R1)は、すべてのパズルにおいて平均失敗位置が一貫して高いことが分かります。これは、一連の動きにおける最初の失敗の平均を示す破線の縦線で示されています。しかし、思考モデルの分布形状は、失敗パターンにおいて概ね高い分散を示しています。これは、これらのモデルが平均的には解のシーケンスをより深く理解できる一方で、推論プロセスがより不安定で、パフォーマンスに一貫性がない傾向があることを示唆しています。

図11: パズル環境における思考型モデルと非思考型モデルの最初の失敗手と問題の複雑さ(N)の比較。上:Claude-3.7-Sonnetとの比較。下:DeepSeek-R1とDeepSeek-V3。
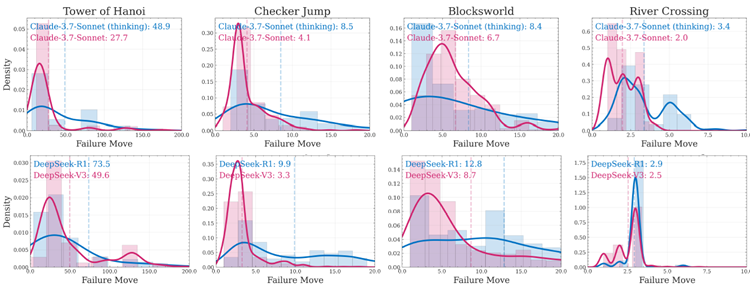
図12: パズル環境における思考型モデルと非思考型モデルの初回失敗手密度分布。上:Claude-3.7-Sonnetとの比較。下:DeepSeek-R1とDeepSeek-V3の比較。
推論努力のダイナミクス。 図 13 は、パズル環境全体での推論努力 (推論思考トークンで測定) と問題の複雑さの関係を示しています。緑の点は正しい解答、赤い十字は誤った解答を示し、青い線はさまざまなパズルと LRM における各複雑さのレベル (N) での思考トークンの平均使用量を追跡しています。3 つの推論モデル (DeepSeek-R1、Claude-3.7-Sonnet-thinking、o3-mini) すべてで一貫したパターンが見られ、思考トークンの使用、つまり推論努力は当初問題の複雑さとともに増加しますが、モデル固有のしきい値に達すると直感に反して減少します。これは、推論に関する LRM の思考プロセスにおける興味深く基本的なスケーリング限界を示唆しています。特定の複雑さのしきい値を超えると、モデルは問題を解決できないだけでなく、より困難な問題に直面し、コンテキストと世代の制限をはるかに下回っているにもかかわらず、直感に反して推論計算が減少します。
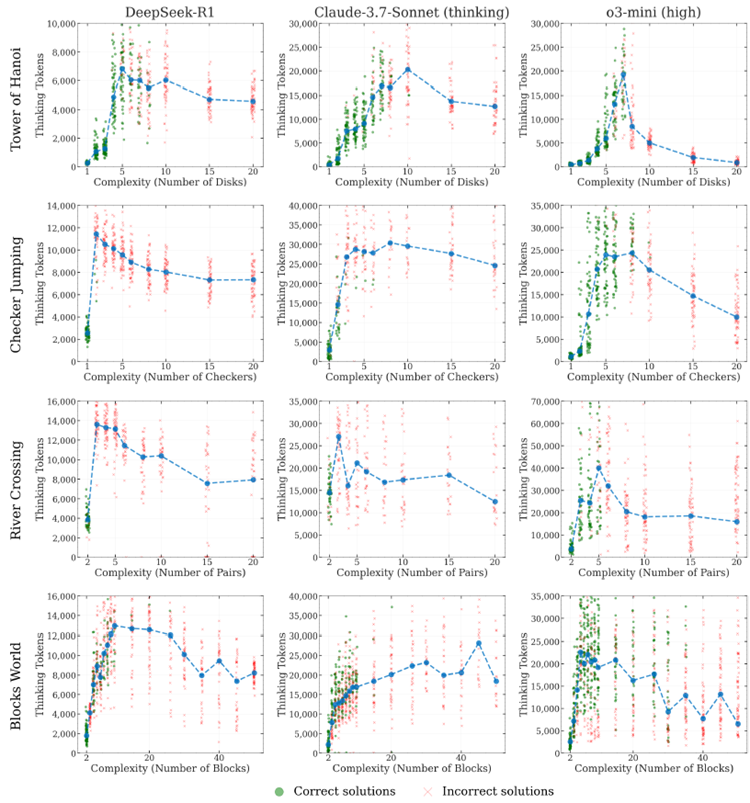
図 13: 4 つのパズル環境における 3 つの LRM (DeepSeek-R1、思考機能付き Claude-3.7-Sonnet、o3-mini) の推論努力 (推論思考トークンで測定) と問題の複雑さ (N) の関係に関する詳細な結果。