ディープニューラルネットワークは、汎化の従来の概念に反するものとして、他のモデルクラスとは異なると見なされることがよくある。異常な汎化動作の一般的な例としては、良性の過剰適合、二重降下、過剰パラメータ化の成功などがある。これらの現象はニューラル ネットワークに特有のものではなく、特に神秘的でもないと我々は主張する。さらに、この汎化動作は直感的に理解でき、PAC ベイズや可算仮説境界などの長年の汎化フレームワークを使用して厳密に特徴付けることができる。これらの現象を説明する重要な統一原理として、ソフトな帰納バイアスを提示する。過剰適合を避けるために仮説空間を制限するのではなく、データと一致するより単純な解をソフトに優先して、柔軟な仮説空間を採用する。この原理は多くのモデルクラスにエンコードできるため、ディープラーニングは見た目ほど神秘的でも他のモデルクラスと異なるものでもない。ただし、ディープラーニングが表現学習の能力、モード接続などの現象、相対的な普遍性など、他の点で比較的異なる点も強調する。
「教科書は書き直さなければならない!」
ディープニューラルネットワークは、汎化に関する従来の常識に反する動作をするため、他のモデルクラスとは異なっており、神秘的であると考えられることがよくある。ディープラーニングが他と異なる点を尋ねられた場合、過剰パラメータ化、二重降下法、良性過剰適合などの現象を指摘するのが一般的である(Zhang 他、2021 年、Nakkiran 他、2020 年、Belkin 他、2019 年、Shazeer 他、2017 年)。
これらの現象はいずれもニューラル ネットワークに特有のものではなく、特に神秘的なものでもないというのが我々の立場である。さらに、VC次元(Vapnik、1998)や Rademacher 複雑性 (Bartlett & Mendelson、2002) などの汎化フレームワークではこれらの現象を説明できないが、PAC-Bayes (McAllester、1999、Catoni、2007、Dziugaite & Roy、2017) などの他の長年使用されているフレームワークや、単純な可算仮説一般化境界 (Valiant、1984、Shalev-Shwartz & Ben-David、2014、Lotfi 他、2024a) では正式に説明されている。言い換えれば、ディープラーニングを理解するために汎化を再考する必要はなく、これまでも必要なかった。
我々の目的は、ディープラーニングが完全に理解されていると主張したり、ディープラーニングの現象を理解するための研究を包括的に調査したり、何らかの現象を説明するための研究に歴史的な優先順位を割り当てたりすることではない。また、これらの現象のいずれかが他のモデルクラスを使用して再現できることを最初に指摘したと主張するつもりもない。実際、ディープラーニングにおける神秘的であるとよく認識されている汎化動作の理解において大きな進歩があったこと、そして一般的な考えに反して、この動作の多くはディープラーニングの外にも適用され、何十年も存在しているフレームワークを使用して正式に説明できることを明確にしたい。教科書が、何十年も前に汎化についてすでに知られていたことに注意を払っていれば、書き直す必要はなかった。代わりに、コミュニティを橋渡しし、進歩を認める必要がある。
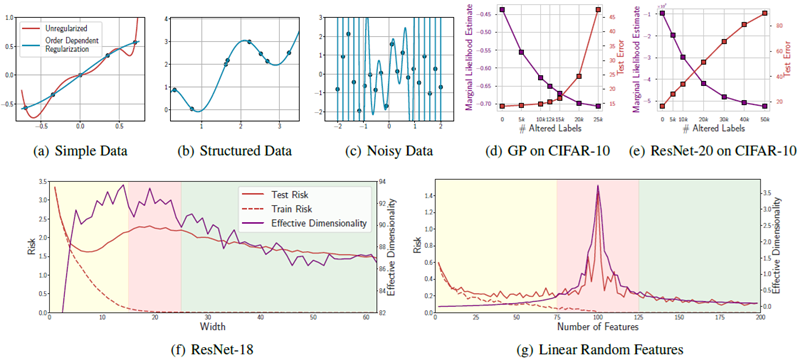
実際、我々は、これらの現象を再現し、その背後にある直感を説明するために、できるだけ単純な例、多くの場合は基本的な線形モデルを紹介することを目指す。特に単純な例に頼ることで、これらの汎化動作はニューラル ネットワークに特有のものではなく、実際には基本的な原理で理解できるという点を強調できると期待している。たとえば、図1では、良性過剰適合と二重降下が単純な線形モデルで再現および説明できることを示している。

図 . ディープラーニングに関連する汎化現象は、単純な線形モデルで再現して理解できる。上: 良性過剰適合。次数依存の正則化を伴う150次多項式は、(a) 単純な構造化データと (b) 複雑な構造化データを合理的に説明すると同時に、(c) 純粋なノイズに完全に適合できる。(d) ガウス過程は、Zhang ら (2016) の CIFAR-10 の結果を正確に再現し、ノイズの多いラベルに完全に適合しながらも、妥当な一般化を達成している。さらに、GP と (e) ResNet の両方で、PAC-Bayes 境界 (Germain ら、2016) に直接対応する周辺尤度は、Wilson & Izmailov (2020) の場合と同様に、変更されたラベルが増えると減少する。下: 二重降下。(f) ResNet と (g) 線形ランダム特徴モデルはどちらも二重降下を示し、Maddox らの場合と同様に、有効次元は低トレーニング損失領域での 2 次降下を厳密に追跡する。(2020年)。
また、ソフトな帰納バイアスという統一概念を通じて、これらすべての現象を集合的に扱う。帰納バイアスは、仮説空間のサイズを制約してデータ効率と一般化を改善する制約バイアスであると考えられることが多いが、制約バイアスは必要ない。代わりに、図3 に示すように、特定の解を他の解よりも優先することを表現するソフトバイアスと組み合わせて、任意の柔軟な仮説空間を採用することができる。PAC-Bayes などのフレームワークは、この帰納バイアスの見方と完全に一致しており、モデルが特定の解を他の解よりも優先する限り、数十億のパラメーターを持つモデルでも空虚でない汎化境界を作成できる (Lotfi ら、2024b)。大まかに言えば、大きな仮説空間と単純な解の優先を組み合わせると、図2 に示すように、優れたパフォーマンスを実現するための証明可能な有用なレシピが提供される。
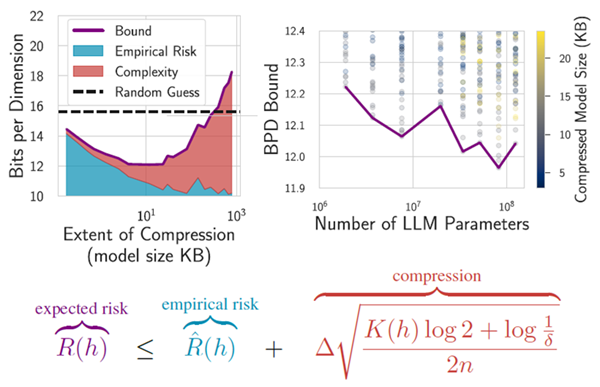
図2. 汎化現象は、汎化境界によって正式に特徴付けることができる。汎化は、セクション 3.1 にあるように、仮説 \(h\) の経験的リスクと圧縮性によって上限を設定できる。コルモゴロフ複雑度 \(K(h)\) で形式化された圧縮性は、モデルのファイル サイズによってさらに上限を設定できる。大規模なモデルはデータに適合するため、小さなファイル サイズに効果的に圧縮できる。Rademacher 複雑度とは異なり、これらの境界は、ノイズに適合できる仮説空間 \(\mathcal H\) を持つモデルにペナルティを課すことはなく、良性の過剰適合、二重降下、および過剰パラメータ化を記述する。上記の Lotfi ら (2024a) のように、LLM に空でない境界を設定することもできる。
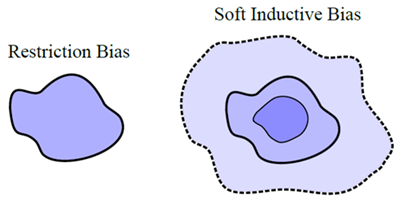
図3. ソフトな帰納バイアスにより、過剰適合せずに柔軟な仮説空間が可能になる。多くの汎化現象は、ソフトな帰納バイアスの概念を通じて理解できる。つまり、モデルが表すことができる解を制限するのではなく、特定の解を他の解よりも優先することを指定する。この概念化では、仮説を完全に制限するのではなく、優先順位の低い仮説を明るい青で示して仮説空間を拡大する。ソフトな帰納バイアスを実装する方法は多数ある。低次の多項式を使用するのではなく、次数依存の正則化を伴う高次の多項式を使用する。または、モデルを並進不変に制限するのではなく (ConvNet など)、圧縮バイアス (ConvNet バイアスを伴うトランスフォーマーや RPP など) によって不変性を優先する。過剰パラメータ化は、ソフトバイアスを実装するもう 1 つの方法である。
また、スケーリング則やグロッキングなど、最近注目されている他の現象もあるが、これらは通常、汎化理論と矛盾するもの、またはニューラル ネットワークに固有のものとして扱われないため、ここでは焦点を当てていない。ただし、セクション 3 の PAC ベイズと可算仮説の汎化フレームワークは、LLM やChinchilla スケーリング則とも一致していることに注目する (Hoffmann ら、2022 年、Finzi ら、2025 年)。さらに、もちろんディープラーニングは他の点では異質で神秘的である。セクション 8 では、表現学習、モード接続性、広く成功しているコンテキスト内学習など、ディープ ニューラル ネットワークの比較的特徴的な機能について説明する。
まず第 2 章でソフト帰納バイアスについて議論する。これは本論文全体を通して統一的な直観を提供する。次に第 3 章で、いくつかの一般的なフレームワークと定義を簡単に紹介する。これらは、次の章で汎化現象を調べるための準備である。本論文全体を通して、第 3.1 章でこれらの汎化現象を特徴付ける PAC-Bayes と可算仮説フレームワークを、第 3.3 章でこれらの汎化現象を特徴付けない Rademacher 複雑性や VC 次元などの他の汎化フレームワークと特に対比する。次に、第 4、5、6 章で良性過剰適合、過剰パラメータ化、二重降下について、第 7 章で代替ビューについて、第 8 章でユニークな特徴と未解決の問題について説明する。
帰納バイアスは制約バイアス、つまり関心のある問題に即した仮説空間への制約であると考えられることがよくある。言い換えると、データに適合して汎化が不十分になる可能性のあるパラメータ設定は多数あるため、検討している問題に対して適切な汎化が得られる可能性の高いパラメータ設定に仮説空間を制限する。さらに、仮説空間が小さいため、新しいデータポイントの追加によって「除外」する解が少なくなり、データによって制約される可能性が高くなる。畳み込みニューラル ネットワークは標準的な例である。MLP から開始し、パラメータを削除してパラメータ共有を強制し、局所性と並進の等価性に対する厳しい制約を提供する。
しかし、制約バイアスは不必要なだけでなく、望ましくないと言えるであろう。我々は、データを説明できるあらゆる解をサポートしたいと考えている。つまり、柔軟な仮説空間を採用するということである。たとえば、データがほぼ並進不変であると疑う場合がある。代わりに、ハード制約なしでモデルを並進不変にバイアスすることができる。ソフトな ConvNet バイアスを提供する素朴な方法は、MLP から始めて、ConvNet に存在しないパラメーターのノルムと、ConvNet で共有されるパラメーター間の距離の両方にペナルティを課す正則化を導入することである。このバイアスは、正則化の強度によって制御できる。残差経路事前分布は、ハードなアーキテクチャ制約をソフトな帰納バイアスに変換するための、より実用的で一般的なメカニズムを提供する (Finzi ら、2021)。
データに同じように適合する場合でも、特定の解を他の解よりも優先するという一般的な考え方を、ソフトな帰納バイアスと呼ぶ。ソフトなバイアスを、仮説空間に厳しい制約を課すより標準的な制約バイアスと対比する。図 3 にソフトな帰納バイアスの概念を示し、図 4 にソフトな帰納バイアスがトレーニング プロセスに与える影響を示す。正則化、およびモデルパラメータに対するベイズ事前分布は、ソフトな帰納バイアスを作成するためのメカニズムを提供する。ただし、正則化は通常、アーキテクチャの制約を緩和するために使用されることはなく、後で説明するように、ソフトなバイアスはより一般的であり、アーキテクチャによって誘発される可能性がある。
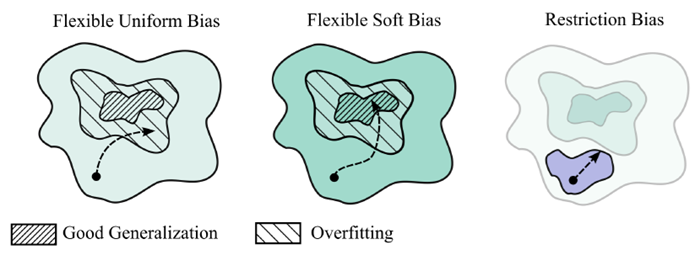
図 4. ソフトな帰納バイアスによる良好な汎化の達成。左: 仮説空間は大きいが、データに同じ適合性を提供する解の間の優先順位がない。そのため、トレーニングは、汎化が不十分な過剰適合解につながることが多い。中央: ソフトな帰納バイアスは、さまざまな色合いで表される解の間の優先順位と組み合わせて柔軟な仮説空間を表すことで、トレーニングを良好な汎化に導く。右: 仮説空間を制限すると、特定の望ましい特性を持つ解のみを考慮することで、過剰適合を防ぐことができる。ただし、表現力を制限することで、モデルは現実のニュアンスを捉えることができず、汎化が妨げられる。
実行例として、大きな多項式を考えてみよう。ただし、高次の係数を低次の係数よりも多く正規化する。言い換えると、データを \(f(x,w)=\sum_{j=0}^Jw_jx^j\) でフィッティングし、\(w_j\) の正規化子は \( j\) とともに強度が増す。最後に、\(f(x,w), p(y|f(x,w))\) を含む尤度から形成されるデータフィッティング項がある。したがって、合計損失は次のようになる。 \[ 損失=データ適合度+次数依存複雑度ペナルティー \] これは、たとえば、\(\mathcal L(w) =−\log p(y|f(x,w)) +\sum_j\gamma^jw_j^2,> 1\) という形式になる。分類の場合、観測モデル \(p(y_i|f(x_i,w)) = softmax(f(x_i,w))\) は、\(−\log p(y|f(x,w))\) のクロスエントロピーになる。回帰では、\(p(y_i|f(x_i,w)) = N(f(x_i,w), σ^2)\) は、\(1/(2σ^2)\) で割った二乗誤差データ適合になる。
多項式 J の次数を大きくすると、柔軟なモデルになる。ただし、モデルには単純化バイアスがある。次数に依存する複雑さのペナルティのため、モデルはできるだけ低次の項を使用してデータを近似し、必要な場合にのみ高次の項を使用する。たとえば、データが直線になる単純な1次元回帰問題を想像してもらいたい。J が大きい場合、データに完全に適合する係数 \(\{w_j\}\) の設定は多数ある。ただし、モデルは、\(j ≥ 2\) に対して \(w_j = 0\) の単純な直線近似を優先する。これは、図1(左上) に示すように、データと一致し、ペナルティが最も低くなるためである。実際には、低次多項式のハード制約バイアスを緩和し、ソフトな帰納バイアスに変えた。このようなモデルは、あらゆるサイズのトレーニングセットにも効果的である。図5に示すように、小さなデータセットでは厳しい制約のあるモデルと競合し、大きなデータセットでは比較的制約のないモデルと競合する。
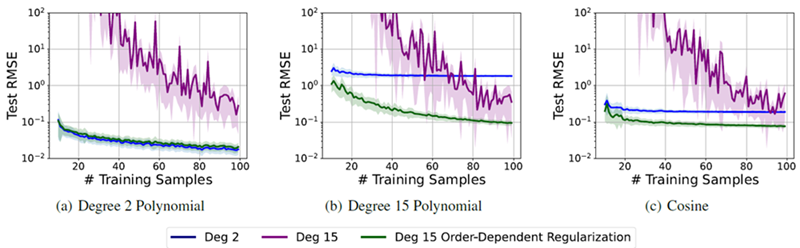
図5. 単純化バイアスによる柔軟性は、さまざまなデータ サイズと複雑さに適している。2 次、15 次、および正規化された 15 次多項式を使用して、(a) ~ (c) で説明した関数から生成されたさまざまなトレーニング データ サイズを持つ 3 つの回帰問題を適合させる。多項式係数の次数とともに増加する特別な正規化ペナルティを使用する。100 個のテスト サンプルの 100 回の適合の平均パフォーマンス ± 1 標準偏差を示す。データに適合させるために必要なだけ複雑さを増やすことで、正規化された 15 次多項式は、すべてのデータ サイズとさまざまな複雑さの問題に対して、他のすべてのモデルと同等かそれ以上の性能を発揮する。
\(ℓ_2\) および \(ℓ_1\) (または Lasso) 正則化は標準的な手法であるが、任意のサイズのモデルを構築するための処方箋としては使用されない。次数依存の正則化の考え方はあまり知られていない。Rasmussen & Ghahramani (2000) は、ベイジアン周辺尤度(証拠)、つまり事前分布からトレーニングデータを生成する確率が、同様の次数依存のパラメーター事前分布を持つ高次フーリエ モデルに有利であることを示している。パラメーター \(p(w)\) の事前分布は、関数 \(p(f(x,w))\) の事前分布を誘導し、ベイジアンの観点からは、モデルの汎化特性を制御するのはこの関数の事前分布である (Wilson & Izmailov、2020)。次数依存の事前分布は、高次モデルの場合でも、データを生成する可能性のある関数の事前分布を生み出す。一方、Rasmussen & Ghahramani (2000)の6年後、標準的な教科書 Bishop (2006) は第 3 章 168 ページで、周辺尤度は小さい多項式や大きい多項式ではなく、中次の多項式を選択するという点で、従来のモデル選択の概念と一致していると主張している。実際には、この教科書の結果は、単に不適切な事前分布の産物である。つまり、等方性パラメーター事前分布 (\(ℓ_2\) 正則化に類似) を使用しており、等方性パラメーター事前分布を持つ高次多項式でデータが生成されそうにない。Bishop (2006) が次数依存の事前分布を選択していたら、周辺尤度は任意の高次モデルを優先していた可能性がある。
残差パスウェイ事前分布(RPP)(Finzi et al.、2021)では、等分散制約のソフトバイアスが、特定の問題に対して完全に制約されたモデルと同じくらい効果的であることが示された。たとえば、回転等分散のソフトバイアスは、回転不変である分子の場合、回転等分散モデルと同様に機能する。モデルは対称性を使用してデータを表すように推奨(制約なし)されており、少量のデータでも正確に表現できるため、ごく少量のデータにさらされると、ソフトバイアスはほぼ完全な回転等分散に収束する。さらに、データに近似対称性しか含まれていない場合、または対称性がまったく含まれていない場合、RPPアプローチは、ハード対称制約を持つモデルよりも大幅に優れている。
驚くべきことに、トレーニング後のビジョン トランスフォーマーは、畳み込みニューラル ネットワークよりもさらに並進不変になる可能性がある (Gruver ら、2023)。ConvNet はアーキテクチャ上、並進不変に制約されているため、この発見は不可能に思えるかもしれない。ただし、実際には、等変はエイリアシング アーティファクトによって破られる。等変対称性は、データを圧縮するためのメカニズムを提供し、後のセクションで説明するように、トランスフォーマーには圧縮のためのソフトな帰納バイアスがある。
仮説空間を制限するのではなく、ソフトな帰納バイアスがインテリジェント システムを構築するための重要な処方箋であるというのが我々の見解である。
これまで我々は、柔軟な仮説空間を直感的に受け入れたいと主張してきた。それは、現実世界のデータは洗練された構造を持つだろうという我々の正直な信念を表しているからである。しかし、優れた汎化を行うためには、どんなタイプの解も許容するとしても、特定のタイプの解に対する事前のバイアスを持たなければならない。我々が議論する汎化現象は、Zhang et al. (2016; 2021) で主張されているように、過剰適合や Rademacher 複雑性などの一般化の概念に関する従来の常識に反しているが、この直感と完全に一致している。
これらの現象は、PAC-Bayes (McAllester、1999; Guedj、2019; Alquier et al.、2024) や単純な可算仮説境界 (Valiant、1984; Shalev-Shwartz & Ben-David、2014) など、何十年も存在している汎化フレームワークによって正式に特徴付けられることも判明した。これらのフレームワークについては、セクション 3.1 で紹介する。次に、セクション 3.2 で有効次元を定義する。これは、直感のためにこの論文の後半で再度説明する。最後に、セクション 3.3 で、これらの現象を説明しないが、汎化についての考え方の従来の考え方に大きな影響を与えたフレームワークを紹介する。
このセクションでは、いくつかの定義と汎化フレームワークを簡単に紹介する。これらは、後のセクションで汎化現象を検討するための準備である。
PAC-Bayes と可算仮説境界は、仮説空間のサイズだけでなく、どの仮説が可能性が高いかに焦点を当てているため、大規模モデルや過剰パラメータ化されたモデルに対しても魅力的なアプローチを提供する (Catoni、2007 年; Shalev-Shwartz および Ben-David、2014 年; Dziugaite および Roy、2017 年; Arora ら、2018b 年; P´erez-Ortiz ら、2021 年; Lotfi ら、2022a 年)。これらは、セクション 2 のソフト帰納バイアスの概念と調和しており、任意の大きさの仮説空間で良好な一般化を達成するためのメカニズムと、データへの適合とは無関係に特定の解を他の解よりも優先するメカニズムを提供する。
定理 3.1 (可算仮説境界)。 有界リスク \(R(h, x) ∈ [a, a + Δ]\) と、事前確率 \(P(h)\) を持つ可算仮説空間 \(h ∈ \mathcal H\) について考える。 経験的リスク \(\hat R(h) = \frac{1}{n}\sum_{i=1}^n R(h, x_i)\) を、固定仮説 h に対する独立確率変数 \(R(h, x_i)\) の合計とする。 \(R(h) = \mathbb E[\hat R(h)]\) を予想されるリスクとしよう。そうすると、少なくとも \(1-\delta\) の確率で \[ R(h)\leq\hat R(h)+\Delta\sqrt{\frac{\log\frac{1}{P(h)}+\log\frac{1}{\delta}}{2n}} \tag{1} \]
この境界は有限仮説境界と関連しているが、事前確率 P(h) と有限仮説空間ではなく可算な仮説空間を含む (Ch 7.3、Shalev-Shwartz & Ben-David、2014)。事前確率は、特定の仮説を他の仮説よりも高く重み付けする重み関数と考えることができる。重要なのは、境界を評価するために任意の事前確率を使用できることである。事前確率は、データの真の仮説を生成する必要はなく、真の仮説を含む必要もなく、仮説 h∗ を見つけるようにトレーニングされたモデルによって使用される必要さえない。モデルが式 (1) を評価するために使用された事前確率とはまったく異なる事前確率を使用する場合、境界は単純に緩くなる。付録 C に、この境界の基本的な証明を含んでいる。
ソロモノフ事前分布P(h) ≤ 2−K(h|A) (ソロモノフ、1964) を通じて有益な境界を導くことができる。ここでKはモデルアーキテクチャAを入力とするhのプレフィックスフリーコルモゴロフ複雑度である。この事前分布を式(1)に代入すると、 \[ \overbrace{R(h)}^{\text{予測リスク}}\leq \overbrace {\hat R(h)}^{\text{経験的リスク}}+\overbrace{\Delta\sqrt{\frac{K(h|A)\log2+\log\frac{1}{\delta}}{2n}}}^\text{圧縮性} \tag{2} \]
仮説 \(h\) のプレフィックスフリーコルモゴロフ複雑度 \(K(h)\) は、固定プログラミング言語で \(h\) を生成する最短プログラムの長さである (Kolmogorov, 1963)。最短プログラムを計算することはできないが、\(K(h|A)\) を操作することで、アーキテクチャとデータによって決定されない定数を事前確率に吸収することができる。次に、プレフィックスフリーから標準コルモゴロフ複雑度に変換して、上限を計算できる。 \[ \begin{align} \log 1/P(h) &\leq K(h/A)\log 2 \tag{3}\\ \\ \leq C(h)&\log 2+2\log C(h) \tag{4} \end{align} \] ここで、\(C(h)\) は、事前に指定されたコーディングを使用して仮説 h を表すために必要なビット数である。したがって、経験的リスクが低く、圧縮サイズが小さい仮説を表す多くのパラメーターを持つ大規模なモデルでも、強力な汎化保証を実現できる。
PAC-Bayes境界は、望ましい解\(Q\)の分布を考慮することで、必要なビット数を\(\log_2\frac{1}{P(h)}\)から\(\mathbb K\mathbb L(Q ‖ P)\)にさらに減らすことができる。サンプリングする\(Q\)の特定の要素にとらわれない場合は、別のメッセージをエンコードするために使用できるビットを回復できる。点質事後確率\(Q\)を持つPAC-Bayes境界は式(1)に似た境界を回復できるため(Lotfi et al., 2022b)、両方の境界をPAC-Bayesと呼ぶことがある。また、モデルの事前分布からトレーニングデータを生成する確率である周辺尤度は、PAC-Bayes境界に直接対応することに注意(Germain et al., 2016; Lotfi et al., 2022b)。
これらの一般化フレームワークは、数百万、あるいは数十億のパラメータを持つモデルに対して、空虚でない汎化保証を提供するように適応されている。これらは決定論的に訓練されたモデルに適用され、また、無制限のビット/次元(トークンあたりのナット数)損失、確率的訓練、およびトークン間の依存性に対応するために LLM にも適応されている(Lotfi et al., 2023; 2024b; Finzi et al., 2025)。さらに、これらの境界の計算は簡単である。たとえば、(i)任意のオプティマイザーを使用して、仮説 \(h^∗\) を見つけるようにモデルを訓練する。(ii)経験的リスク \(\hat R(h^∗)\) を測定します(例:訓練損失)。(iii)\(C(h^∗)\) の保存されたモデルのファイルサイズを測定する。(iv)式(4)を式(2)に代入する。
言葉で言えば、これらの汎化限界は次のように解釈できる。 \[ 予測リスク ≤ 経験的リスク+ モデル圧縮性 \] ここで、圧縮性は複雑性の形式化を提供する。Lotfi et al. (2023) から改変した図 2 では、各項が境界にどのように寄与するかを視覚化している。この境界の表現は、汎用学習器を構築するための処方箋も提供する。柔軟な仮説空間と低いコルモゴロフ複雑性への偏りを組み合わせることである。柔軟なモデルは、さまざまなデータセットで低い経験的リスク (トレーニング損失) を達成できる。これらのモデルを圧縮できることは、優れた汎化につながることが証明されている。Goldblum et al. (2024) は、ニューラル ネットワーク、特に大規模なトランスフォーマーは低いコルモゴロフ複雑性に偏りがちであり、実際のデータ上の分布も同様であることを示している。このため、単一のモデルで多くの実際の問題に対して優れた汎化を実現できる。
実際、すべての可能なプログラムで構成される最大限に柔軟な仮説空間内であっても、データに適合し複雑性が低い仮説を選択した場合は、式 (1) の可算仮説境界によって一般化することが保証される。この洞察は、ソロモンオフ帰納法に関連付けることができる。ソロモンオフ帰納法は、仮説が持つことができる複雑性やパラメータの数に制限がなく、理想的な学習システムを形式化する、最大限に過剰パラメータ化された手順を提供する (Solomonoff、1964 年、Hutter、2000 年)。より単純な (短い) プログラムに指数関数的に高い重みを割り当てることにより、ソロモンオフ帰納法は、仮説空間が巨大であっても、データに適合する場合は選択された仮説が単純であることを保証する。
一般的に、PACBayes と可算仮説境界についてはよくある誤解がある。たとえば、それらはパラメータの分布だけでなく、決定論的なパラメータを持つモデルに適用される。さらに、最近の境界は、モデルが大きくなるにつれて緩くなるのではなく、厳しくなる。付録 A では、いくつかの誤解について説明する。また、これらの境界は大規模なニューラル ネットワークに対して空虚ではないだけでなく、驚くほど厳しい場合もあることにも注目に値する。たとえば、Lotfi ら (2022a) は、CIFAR-10 で数百万のパラメータを持つモデルの分類誤差の上限を 16.6% とし、確率は少なくとも 95% としているが、これはこのベンチマークではかなり立派なパフォーマンスである。
有効次元は、汎化現象を説明するのに役立つ直感を提供する。行列 \(A\) の有効次元は \(N_{eff}(A) =\sum_i\frac{λ_i}{λi+α}\) である。ここで、\(λ_i\) は \(A\) の固有値、\(α\) は正則化パラメーターである。有効次元は、比較的大きな固有値の数を計測する。パラメーター \(w\) について評価された損失のヘッシアンの有効次元は、損失ランドスケープ内の鋭い方向の数、つまりデータから決定されるパラメーターの数を計測する。
有効次元数が低い解はより平坦であり、つまり、損失を大幅に増やすことなく、関連するパラメータを乱すことができる。平坦性は汎化に影響を与える唯一の要因ではなく、ヘッセ行列で測定される平坦性はパラメータ化不変ではない(SGD、\(ℓ_2\) 正則化、および多くの標準的な手順のように)。つまり、より平坦な解がより一般化されない例を簡単に見つけて構築できる(例:Dinh et al.、2017)。一方、平坦性と汎化の関係は、偽りの経験的関連ではない。平坦性がより良い汎化につながる理由については、メカニズム的な理解がある。より平坦な解は、より圧縮可能で、より優れたオッカム因子を持ち、より広い決定境界とより狭い汎化境界につながる傾向がある (Hinton & Van Camp、1993 年; Hochreiter & Schmidhuber、1997 年; MacKay、2003 年; Keskar 他、2016 年; Izmailov 他、2018 年; Foret 他、2020 年; Maddox 他、2020 年)。
ラデマッハ複雑度と同様に、有効次元はそれ自体が汎化境界ではないが、汎化境界に正式に組み込むことができる直感的な量である (MacKay、2003; Dziugaite & Roy、2017; Maddox et al.、2020; Jiang et al.、2019)。また、モデルの有効ランク (Bartlett et al.、2020) やずさんなモデル (Quinn et al.、2022) など、汎化現象を説明する際に頻繁に登場する他の概念とも密接に関連している。
汎化現象について議論するときには、直感的な有効次元に戻ることがよくある。
Rademacher 複雑度 (Bartlett & Mendelson, 2002) は、モデルが均一な \(\{+1,−1\}\) ランダム ノイズに適合する能力を正確に測定する。同様に、VC 次元 (Vapnik ら、1994) は、仮説空間 \(\mathcal H\) が \(\{+1,−1\}\) ラベルを持つ任意の d ポイント セットに適合 (「粉砕」) できる最大の整数 d を測定する。fat-shattering 次元 (Alon ら、1997) \(fat_γ(\mathcal H)\) は、VC 次元を、マージン \(γ\) で適合 (「粉砕」) ラベルに洗練する。 PAC-Bayesとは異なり、これらすべてのフレームワークは、全体的な仮説空間\(\mathcal H\)のサイズにペナルティを課し、セクション2のソフトな帰納バイアスではなく、制限バイアスの処方を示唆している。これらのフレームワークについては付録Bでさらに詳しく説明し、表1に比較の概要を示す。
良性の過剰適合とは、モデルが損失なくノイズに適合し、構造化データに対しても汎化できる能力を指す。これは、モデルがデータに過剰適合する可能性があるが、構造化データに対して過剰適合する傾向がないことを示している。論文「understanding deep learning requires re-thinking generalization (ディープラーニングを理解するには、汎化の再考が必要)」(Zhang et al., 2016) は、畳み込みニューラル ネットワークがランダム ラベルの画像に適合できるが、CIFAR などの構造化画像認識問題に対しては一般化が優れていることを示して、この現象に大きな注目を集めた。この結果は、VC 次元や Rademacher 複雑性などのフレームワークに基づき、ニューラル ネットワークに特有の汎化に関する知識と矛盾するものとして提示された。著者らは、「これらの巨大なモデルが単純になる正確な正式な尺度はまだ発見されていないと主張する」という主張で結論付けた。5 年後、著者らは同じ立場を維持しており、「understanding deep learning (still) requires re-thinking generalization (ディープラーニングを理解するには (依然として) 一般化の再考が必要)」(Zhang et al., 2021) と題する拡張論文を発表している。同様に、Bartlett et al. (2020) は、「良性過剰適合の現象は、ディープラーニング手法によって解明された重要な謎の 1 つである。ディープ ニューラル ネットワークは、ノイズの多いトレーニング データに完全に適合していても、適切に予測できるようである。」と述べている。
しかし、良性の過剰適合動作は他のモデル クラスでも再現でき、直感的に理解でき、数十年にわたって存在してきた汎化を特徴付ける厳密なフレームワークによって説明できる。直感的に、良性の過剰適合を再現するには、柔軟な仮説空間と、データに適合することを要求する損失関数、および単純さのバイアスが必要である。データと一致する(つまり、データに完全に適合する)解の中で、より単純なものが好まれる。ここで、回帰と、セクション 2 の次数依存正則化を使用した単純な多項式モデルについて考えてみよう。尤度では、σ を小さな値にするため、モデルはデータの適合を優先する(二乗誤差に大きな数を掛ける)。ただし、係数のノルムは係数の次数とともにペナルティが大きくなるため、モデルはより低い次数の項を使用することを強く好む。単純な構造のデータは、汎化する単純な構造の圧縮可能な関数に適合されるが、モデルは、図 1 (上) に示すように、純粋なノイズを含むデータに適合するために必要に応じて複雑さを調整する。言い換えれば、ディープラーニングを理解するには汎化を再考する必要があるとすれば、この単純な多項式を理解するのも同様に必要である。なぜなら、この多項式は良性の過剰適合を示しているからである。
正式な汎化フレームワーク。良性過剰適合は、PAC ベイズと可算仮説境界によっても特徴付けられる。これらは、汎化を特徴付けるための正式かつ長年使用されているフレームワークである。良性過剰適合を示すニューラル ネットワークに対してこれらの境界を評価でき、空虚でない汎化保証を提供する (Dziugaite & Roy、2017 年; Zhou ら、2018 年; Lotfi ら、2022a 年)。さらに、セクション 3 で説明するように、これらの一般化フレームワークは、コルモゴロフ複雑度を通じて、大規模なニューラル ネットワークがどれだけ単純であるかを正確に定義できる。実際、大規模なニューラル ネットワークは、低いコルモゴロフ複雑度のソリューションに対してさらに強い偏りを持つことがよくある (Goldblum ら、2024 年)。
信号とノイズの混合。信号とノイズの混合に適合しながらも十分な一般化を達成する能力も再現可能であり、セクション 3.1 の一般化フレームワークによって特徴付けられる。特に、Wilson & Izmailov (2020) に従って、図 1(d)(e) の CIFAR-10 に対する Zhang et al. (2021) の混合ノイズラベル実験を正確に再現できる。ここでは、ガウス過程 (GP) が、トレーニング エラーなしで変更されたラベルの数が増える CIFAR-10 に適合される。汎かは妥当であり、変更されたラベルの数が増えるにつれて着実に低下する。重要なことは、GP と ResNet の両方の周辺尤度が減少し、周辺尤度が PAC-Bayes の一般化境界 (Germain et al.、2016) と直接一致することである。
良性過剰適合に関する研究。現在までに、良性過剰適合を他のモデル クラスで研究し、再現する研究が多数行われている。しかし、良性過剰適合は謎に包まれたディープラーニング特有の現象であり、一般化を再考する必要があるという従来の認識は根強く残っている。ここでこの研究のすべてを網羅することは意図しておらず、不可能でもあるが、いくつかの重要な進展について言及する。Dziugaite & Roy (2017) は、構造化 MNIST とノイズの多い MNIST でトレーニングされたニューラル ネットワークの非空虚 PAC-Bayes 境界と空虚 PAC-Bayes 境界をそれぞれ示している。Smith & Le (2018) は、MNIST でのロジスティック回帰の良性過剰適合を実証し、ベイジアン オッカム係数 (MacKay、2003) を使用して結果を解釈している。いくつかの研究は、2 層ネットワークを分析している (例: Cao et al., 2022; Kou et al., 2023)。Wilson と Izmailov (2020) は、ガウス過程とベイジアン ニューラル ネットワークを使用して Zhang et al. (2016) の実験を正確に再現し、限界尤度を使用して結果を説明しているる。Bartlettら (2020) は、線形回帰モデルが良性の過剰適合を再現できることを示している。彼らは、データ共分散行列のランクと最小ノルム最小二乗解を研究することでこの現象を理解している。これは、Maddoxら(2020) が実効次元を通じて二重降下を説明する方法に関連している。この推論については、次のオーバーパラメータ化と二重降下に関するセクションで取り上げる。
結論 ディープラーニングを理解するには(依然として)汎化の再考が必要(Zhang et al., 2021)は、次のようなテストを提案している。「汎化の尺度とされるものについて、自然データとランダム化データでどのように機能するかを比較できるようになった。両方のケースで同じ結果になった場合、自然データからの学習(汎化が可能な場合)とランダム化データからの学習(汎化が不可能な場合)を区別することさえできないため、汎化の良い尺度である可能性はない。」PAC-Bayesと可算仮説境界は明らかにこのテストに合格し、「これらの巨大なモデルが単純になる正確な正式な尺度」も提供するが、Rademacher複雑度とVC次元はそうではない。さらに、この汎化の動作は、圧縮バイアスと組み合わされた柔軟な仮説空間を採用したソフト帰納バイアスの観点から直感的に理解できる。
ソフトバイアスと良性の過剰適合について説明したので、多くのパラメータを持つモデルが必ずしもデータに過剰適合するわけではないことがますます直感的にわかるようになってきている。パラメータのカウントは、一般的に、モデルの複雑さを表すのに適していない。実際、2012 年にディープラーニングが復活する前は、多くのパラメータを持つモデルを採用することが一般的になりつつあった。「現在では、ベイズ主義者がデータポイントの数よりも多くのパラメータを持つモデルを適合させることが一般的な方法になっている...」(MacKay、1995 年)。
我々が関心があるのは、パラメータ単独ではなく、パラメータがデータに適合させるために使用する関数の特性をどのように制御するかである。単純性バイアスがある限り、任意に大きな多項式がデータに適合しすぎないことはすでに説明した。ガウス過程も説得力のある例を提供する。RBF カーネルを持つ GP は、密に分散したラジアル基底関数 \(\phi_i: f(x,w) =\sum_{i=1}^\infty w_i\phi_i(x)\) の無限和から導出できる (MacKay、1998)。同様に、中心極限定理の議論を使用して、無限の単層および多層ニューラル ネットワークに対応する GP カーネルを導出できる (Neal、1996b、Lee ら、2017) (これらの最初のものは悪名高い NeurIPSリジェクトである!)。実際、GP は一般的に標準的なニューラル ネットワークよりも柔軟性が高いが、強い (しかしソフトな) 単純性バイアスにより、小規模なデータセットでは他のモデル クラスと比較して最も優れたパフォーマンスを発揮することがよくある。
過剰パラメータ化が実際に驚くべきことかどうかについては、ほとんど合意が得られていないようである。一方で、任意の数のパラメータを持つモデルは汎化できることは、特定の分野では知られており、理解されている。実際、大規模モデルの限界を追求することは、数十年にわたってノンパラメトリックの指針となっている (例: MacKay、1995 年、Neal、1996a、Rasmussen、2000 年、Rasmussen & Ghahramani、2000 年、Beal 他、2001 年、Rasmussen & Ghahramani、2002 年、Griffiths & Ghahramani、2005 年、Williams & Rasmussen、2006 年)。同時に、過剰パラメータ化は、ニューラル ネットワークの特徴となっている。そして、多くの論文、特に理論論文は、良性過剰適合の観点から、データポイントよりも多くのパラメータを持つディープニューラルネットワークが汎化できることに驚きの声を上げて始まる。たとえば、「ディープネットの謎は、トレーニングサンプルの数よりもはるかに多くのパラメータを持っているにもかかわらず、汎化することである...」(Aroraら、2018a)。さらに、パラメータの数が増えるにつれて、多くの汎化境界も次第に緩くなり、最終的には空虚になる(Jiangら、2019)。
しかし、最近では、パラメータの数が増えるにつれて汎化の境界が狭くなることもある (Lotfiら, 2022a; 2024b)。LLM は多くの場合過剰パラメータ化されていないが、パラメータカウントはこれまで以上に普及している。また、二重降下法 (セクション 6) のプレゼンテーションは、多くの場合、パラメータカウントに基づいている。
理由は 2 つある。柔軟性と圧縮である。柔軟性が高く、圧縮バイアスのあるモデルが、優れた汎化を実現することが証明されている理由についてはすでに説明した (セクション 3)。ニューラル ネットワークのパラメーターの数を増やすと、柔軟性が単純に高まる。おそらくもっと驚くべきことに、パラメーターの数を増やすと、圧縮バイアスも増加する。つまり、パラメーターが多いモデルは、トレーニング後にパラメーターが少ないモデルよりも、メモリ合計を少なくして保存できる。
Maddox ら (2020) は、ヘッセ行列の有効次元を測定することで、トレーニング後のモデルが大きいほど、小さいモデルよりも有効なパラメータが少なくなることを発見した (セクション 3.2)。 最近の研究では、Goldblum ら (2024) も、言語モデルが大きいほど単純性バイアスが強くなり、コルモゴロフ複雑度が低いシーケンスが生成され、このバイアスが複数の異なる設定やモダリティにわたる優れたパフォーマンスとコンテキスト内学習の重要な特徴であることを示している。
しかし、なぜモデルが大きいほど圧縮バイアスが強くなるのだろうか。これは興味深い未解決の問題であるが、いくつかの手がかりと直感がある。Bartlett ら (2020) は、過剰パラメータ化された最小二乗モデルは、有効ランクの低い小ノルムのソリューションをますます好むことを示している (詳細はセクション 6 を参照)。パラメータの数を増やすと、損失ランドスケープ内のフラット ソリューションのボリュームも指数関数的に増加し、より簡単にアクセスできるようになる (Huang ら、2019)。これは、モデルが大きいほど有効次元が小さくなるという経験的裏付けがある (Maddox ら、2020)。これは、一般に信じられていることとは反対に、確率的最適化の暗黙のバイアスがディープラーニングの汎化に必要でない理由も説明するのに役立つ。一部のパラメータ設定がデータに過剰適合している場合でも、データに適合し、汎化も適切に行われるパラメータ設定のボリュームは、その数を大幅に上回る。実際、Geiping ら (2021) は、フルバッチ勾配降下法が大規模な残差ネットワークのトレーニングにおいて SGD とほぼ同等のパフォーマンスを発揮できることを発見し、Chiang ら (2022) はさらに、推測と確認 (パラメータ ベクトルをランダムにサンプリングし、損失の少ないソリューションが見つかったら停止する) でも、確率的トレーニングによる競争力のある汎化を提供できることを示した。
柔軟性と帰納バイアスの間には緊張関係があるように思われることが多く、より柔軟なモデルは帰納バイアスが弱いはずだという想定がある。しかし、これまで見てきたように、柔軟性と帰納バイアスの間にトレードオフが必ずしもあるわけではないだけでなく、より大規模でより柔軟なモデルは、図 6 に示すように、より強い帰納バイアスを持つことがよくある。
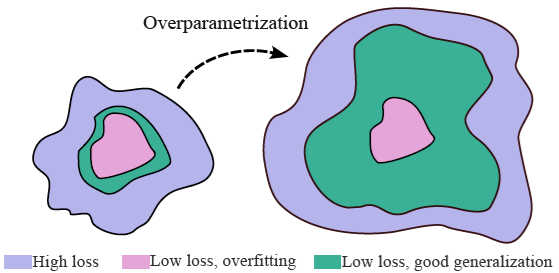
図 6. パラメータを増やすと汎化が向上する。パラメータの数を増やすと、通常、データのより単純な圧縮可能な説明を提供するフラット解が、仮説空間全体の相対的なボリュームをより多く占めるようになり、これらの単純な解に対する暗黙のソフトな帰納バイアスにつながる。過剰パラメータ化されたモデルは、多くの場合、データに過剰適合する仮説 (パラメータ設定など) を多く表が、データによく適合し、優れた汎化を提供する仮説をさらに多く表すこともできる。過剰パラメータ化により、仮説空間のサイズと単純なソリューションに対するバイアスが同時に増加する可能性がある。
二重降下法とは、モデルパラメータの数が増えるにつれて、汎化誤差(または損失)が減少、増加、そして再び減少することを指す。トレーニング損失は、通常、2 回目の降下の開始時にほぼゼロになる。最初の減少とその後の増加は、「古典的なレジーム」に対応する。このレジームでは、モデルは最初はデータ内のより有用な構造を捕捉し、汎化を改善するが、その後、データに過剰適合し始めます。「二重降下法」という名前が付けられた 2 回目の降下法は、「現代の補間レジーム」と呼ばれる。
二重降下法は、Belkin ら (2019) によって現代の機械学習コミュニティに導入され、Nakkiran ら (2020) ではディープ ニューラル ネットワーク向けに重点的に研究された。 これはディープラーニングの大きな謎の 1 つとみなされることが多く、2 回目の降下法は汎化に関する従来の常識に挑戦している。モデルの柔軟性を高めることで従来のレジームで過剰適合が生じている場合、柔軟性をさらに高めることで過剰適合を緩和できるのだろう?Belkin ら (2019) は、二重降下法が「歴史的に存在しない」理由についても推測している。
しかし、二重降下法は、現代のディープラーニング現象とは言えない。 二重降下法の元々の導入は、驚くべきことに、少なくとも Opper ら (1989) の 30 年前にまで遡り、Opper ら (1990)、LeCun ら (1991)、B¨os ら (1993) でも発表されている。また、他のモデル クラスを使用して理解および再現することもできる。実際、Belkin ら (2019) の論文自体が、2 層完全接続ニューラル ネットワークに加えて、ランダム フォレストとランダム フィーチャ モデルを使用した二重降下法を実証している。
二重降下法も理解できる。パラメータの数が増えると、最初はデータに適合する能力が向上し、学習したパラメータの有効次元が高くなる (セクション 3.2)。パラメータの数が増えて、すべてが完全なデータ適合を実現するパラメータ設定の中から選択するようになると、損失の値はどのパラメータを選択するかを決定する要因ではなくなる。パラメータの数を増やし続けると、フラットな解の量が増え、トレーニング中にこれらの解がより発見しやすくなる。したがって、解の有効次元は減少し、一般化が向上する。
この説明は線形モデルとニューラル ネットワークの両方に当てはまるが、線形モデルではさらに詳しい情報を得ることができる。\(Xw = y\) があるとする。ここで、\(X\) は特徴の \(n × d\) 行列、w は d 個のパラメータ、y は n 個のデータ ポイントである。\(d > n\) になると、モデルは無限のパラメータ設定 \(w\) を使用してデータを完全に補間できる。d が増加し続けると、未決定のパラメータの数と損失の平坦な方向が増加する。最小二乗解は \(w^∗ = (X^⊤X)^{−1}X^⊤y\) である。\(d > n\) の場合、ヘッセ行列 \(X^⊤X\) の非ゼロの固有値は最大で n 個ある。 d が増加し続けると、信号はより多くのパラメータに分散され、個々のパラメータがそれほど強く決定されなくなり、有効な次元が減少する。代わりに、\(w^∗\) は最小の \(ℓ_2\) ノルム解を提供し、主に特徴空間で最も情報量の多い方向に依存するより単純なモデルを優先する (Bartlett 他、2020)。良性の過剰適合と同様に、これらの単純さの概念は、可算仮説または PAC ベイズ境界を使用して正式に特徴付けることができる。
Maddox ら (2020) に従い、図 1 (下) では、ResNet-18 と線形モデルの二重降下法を示している。ResNet では、各層の幅を増やすにつれて CIFAR-100 でクロスエントロピー損失が見られる。線形モデルの平均二乗誤差を示している。線形モデルでは、弱情報特性 \(y + \epsilon\) を使用する (\(\epsilon∼\mathcal N(0, 1)\))。どちらも同様の傾向を示している。つまり、有効次元は補間レジームまで増加し、その後減少し、その時点で汎化と有効次元が一致する。
Lotfiら (2022a、図 7) のように、正式な PACBayes 境界を使用して二重降下を追跡することも可能である。2 回目の降下では、より大きなモデルで同様の経験的リスクを達成するが、より圧縮性が高くなる可能性がある。

図7. ニューラル ネットワーク ランドスケープのモードは曲線に沿って接続されている。ネットワークの重みの関数として、CIFAR-100 上の ResNet-164 の ℓ2 正規化クロスエントロピー損失ランドスケープの 3 つの異なる 2 次元サブスペース。水平軸は固定されており、2 つの独立してトレーニングされたネットワークの最適値に固定されているが、垂直軸はパネルごとに異なる。左: 従来の孤立した最適値の仮定。中央と右: ほぼゼロの損失を維持しながら、最適値が単純な曲線で接続される代替平面。モードの接続性は、ディープ ニューラル ネットワークとは比較的異なる。図は Garipov ら (2018) から引用。
もう一つの見解は、良性過剰適合、二重降下、過剰パラメータ化は、主に現代のディープラーニングの現象であり、汎化を再考する必要があるというものである。
そもそも、この、もう一つの見解(かなり主流である!)はどのようにして生まれたのだろう?
バイアスと分散のトレードオフは、データ生成分布上の予想される汎化損失を、予想されるデータ適合度 (バイアス) と適合度間の予想される二乗差 (分散) に分解する。制約付きモデルはバイアスが高く分散が低い傾向があり、制約なしモデルはバイアスが低く分散が高い傾向があり、二重降下の古典的なレジームにおける「U 字型」曲線を示唆している。したがって、教科書では確かに「トレーニング エラーがゼロのモデルはトレーニング データに過剰適合しており、通常は汎化が不十分である」と警告している (Hastie ら、2017 年)。しかし、「トレードオフ」は誤った呼び方である。セクション 2 の次数依存多項式などのモデルや、アンサンブル (Bishop、2006 年、Wilson と Izmailov、2020 年) は、バイアスが低く分散が低い場合がある。
関数クラスが均一な ±1 ラベルに適合する能力を測定する Rademacher 複雑度は、良性の過剰適合を実行するモデルにとって意味のある汎化境界にはつながらない。同様の推論は、VC と脂肪粉砕次元にも当てはまる。しかし、最近の回顧録「...汎化の再考が依然として必要」(Zhangら, 2021) でも、PAC-Bayes に関する文は 1 つしかない。「学習アルゴリズムがパラメータ上の分布を出力できる場合、新しい汎化境界も導出された」。セクション 3 で説明したように、PAC-Bayes と可算仮説境界は、決定論的にトレーニングされたモデルに適用できる。さらに、この汎化動作の厳密な概念的理解を提供し、何十年も存在している。境界の背後にある基本的な考え方は、Shalev-Shwartz & Ben-David (2014、第 7.3 章) などの有名な教科書にも記載されている。ただし、これらのフレームワークは広く知られていたわけではなく、内部化されていなかったため、大規模ネットワーク上の非空境界としての決定論的バリアントは、Lotfi ら (2022a) など、やや後になってからより目立つようになった。
ニューラル ネットワークの暗黙的な正則化は、たとえば、次数依存の正則化を伴う大きな多項式の実行例とは異なる。ただし、どちらのタイプの正則化もソフトな帰納バイアスの例であり、ニューラル ネットワークのサイズを大きくすると暗黙的な正則化が増加する可能性があることを説明した。さらに、この暗黙的な正則化はセクション 3 の汎化フレームワークに反映され、有効次元などの量によって特徴付けられる。暗黙的な正則化はニューラル ネットワークに固有のものではなく、セクション 6 のランダム フィーチャ線形モデルに適用される。さらに、従来の常識に反して、確率的最適化の暗黙的な正則化は、セクション 5 で説明したように、ディープラーニングの汎化で大きな役割を果たす可能性は低い。一方、スケールやその他の要因がニューラル ネットワークの暗黙的な正則化にどのように、なぜ影響するかを正確に理解するのはまだ初期段階である。
全体として、これらの現象は確かに興味深く、(さらに)研究する価値がある。しかし、これらは、よく言われるように、既知のあらゆる汎化フレームワークでは説明できないものではなく、ディープラーニングに特有のものでもない。
これらの現象がディープ ニューラル ネットワークに特有のものではないとしたら、何が特有のものなのか?
ディープ ニューラル ネットワークは他のモデル クラスとは明らかに異なり、多くの点で十分に理解されていない。その実証的なパフォーマンスだけでも、他のモデルとは一線を画している。実際、深層畳み込みニューラル ネットワークと ImageNet の次なる主要アプローチとの間のパフォーマンスの大きな差が、このモデル クラスへの新たな関心 (およびその後の優位性) の原因となっている (Krizhevsky 他、2012)。しかし、実際には、オーバーパラメータ化、良性過剰適合、または二重降下法によって区別されないのであれば、これらのモデルの違いは何だろうか?
最後に、ニューラル ネットワークに比較的特徴的な、特に顕著な特性と汎化動作のいくつか (もちろんすべてではない) を簡単に説明する。
ニューラル ネットワークを他のモデル クラスと区別する主な要素は、表現学習である。表現学習とは実際には何を意味するのだろう?
ほとんどのモデル クラスは、パラメータ \(w\) と基底関数 \(\varphi\) の内積として表現できる: \(f(x,w) = w^⊤\varphi(x)\)。関数クラスは非常に柔軟で (場合によってはメモリに収まるニューラル ネットワークよりも柔軟) (Williams & Rasmussen、2006)、基底関数は非線形であるが、基底関数は通常、事前に固定されている。たとえば、多項式基底、フーリエ基底、またはラジアル基底を使用している場合がある。ラジアル基底の幅などのいくつかのハイパーパラメータ以外、基底関数は通常、データから学習される独自のパラメータをあまり持たない。対照的に、ニューラル ネットワークは、適応型基底を指定する: \(f(x,w) = w^⊤\varphi(x, v)\)。ここで、\(v\) は、学習する比較的大きなパラメーター 集合 (ニューラル ネットワークの重み) であり、基底関数の形状を大幅に制御する。これは通常、点ごとの非線形性 \(σ: f(x,w) = W_{p+1}σ(W_p . . . σ(W_2σ(W_1x)) . . . )\) を通過する連続的な行列乗算を含む階層的な定式化を通じて行われる。ここで、\(\varphi(x, v) = σ(W_p . . . σ(W_2σ(W_1x)) . . . )\)、および \(v = W_1, . . . ,W_p\) である。
一見すると、基底関数を学習する必要はないように思えるかもしれない。結局のところ、セクション 5 で見たように、カーネルを介して固定基底関数で必要なだけの柔軟性 (普遍的な近似値) を実現できる。しかし、基底関数を学習することで、カーネル (特定の問題に対する類似性メトリック) を効果的に学習していることになる。類似性メトリックを学習できることは、ユークリッド距離などの類似性の標準的な概念が破綻する高次元の自然信号 (画像、音声、テキストなど) にとって非常に重要である。類似性学習としての表現学習というこの概念は、モデリングの標準的な基底関数の観点を超えている。たとえば、これは k 近傍法 (knn) などの手順にも当てはまる。k 近傍法では、パフォーマンスは固定距離尺度の選択に左右されるが、理想的には固定距離尺度を学習することができる。1 k 近傍法は基底関数ビューから導出できるが、最も自然な解釈ではない。
1 k 最近傍は基底関数ビューから導き出すことができるが、これは最も自然な解釈ではない。
表現学習の簡単な例を考えてみよう。顔の向きの角度を予測したいとする。同じような向きの角度を持つ顔は、ピクセルの強度のユークリッド距離が大きく異なる場合がある。しかし、ニューラル ネットワークの内部表現は、手元のタスクでは、それらを同じように表現する必要があることを学習できる。言い換えると、同じような向きの角度を持つ顔の場合、生の入力ではなく、深層間のユークリッド距離は類似する。類似性メトリックを学習するこの能力は、外挿、つまりデータから遠く離れた予測を行うために必要である。生の入力のユークリッド距離は、補間がうまく機能するのに十分な密度で分散されたデータ ポイントがあれば、まったく問題ない。59 度と 61 度の回転の例が多数ある場合、補間は 60 度の回転を予測するのに十分に機能する。しかし、表現学習を通じて、ニューラル ネットワークは、遠い角度だけを見ても 60 度の回転を正確に予測できるようになる (Wilson 他、2016)。
ただし、表現学習はニューラル ネットワークに固有のものではない。カーネル メソッドではできないことをニューラル ネットワークで実行できるという主張を目にすることは珍しくない (例: Allen-Zhu & Li、2023)。ほとんどの場合、これらの対比は暗黙的にカーネルが固定されていることを前提としている。しかし、実際にはカーネル学習は豊富な研究分野である (Bach 他、2004 年、G¨onen & Alpaydın、2011 年、Wilson & Adams、2013 年、Wilson 他、2016 年、Belkin 他、2018 年、Yang & Hu、2020 年)。また、カーネル メソッドとニューラル ネットワークを競合するものと見なす必要はない。実際、それらは非常に補完的である。カーネル メソッドは、無限の数の基底関数を持つモデルを使用するメカニズムを提供し、ニューラル ネットワークは、適応型基底関数のメカニズムを提供する。適応基底関数を無限に持つことができない理由はない。ディープカーネル学習 (Wilson 他、2016) はまさにこの橋渡しを提供し、ここで検討した方向角の問題で最初に実証された。
このアプローチでは、ネットワークを 1 回通過するだけで認識論的不確実性表現を実現できるという関心が最近再び高まっている。
ニューラル ネットワークは、表現学習を行う唯一の方法ではない。たとえば、低次元空間では、カーネル学習のメカニズムとしてスペクトル密度を補間する (データの顕著な周波数を学習する) ことが効果的な場合がある (Wilson & Adams、2013 年、Benton ら、2019 年)。
しかし、ニューラル ネットワークは、特に高次元で、適応基底関数を学習する比較的効率的な方法である。その理由も完全には明らかではない。ニューラル ネットワークは距離の概念を学習するだけでなく、この距離の尺度は入力空間 \(x\) 内の位置に応じて変化する。つまり、非定常である。非定常メトリック学習は、データとよく一致する特定の仮定を行わないと非常に困難であることが知られている (Wilson & Adams、2013)。基本的に、ニューラル ネットワークはデータの階層表現を提供し、これらの階層は多くの場合、現実世界の問題の自然な表現である。次のセクション 8.2 で説明するように、ニューラル ネットワークは、自然なデータ分布とよく一致する可能性のある低いコルモゴロフ複雑度に対する強いバイアスも提供する。
歴史的には、特定の問題設定に制約された仮定を持つ専門の学習器を構築するのが常識だった。たとえば、分子をモデル化する場合、回転不変性をハードコードし、ドメインの専門家と話し合って、モデルに課したい他の制約を理解することができる。このアプローチは、多くの場合、ノーフリーランチ定理 (Wolpert、1996 年、Wolpert と Macready、1997 年、Shalev-Shwartz と Ben-David、2014 年) に由来している。この定理では、すべてのモデルは、均一に抽出されたすべてのデータセットに対して期待値において同等に優れているとされている。これらの定理は通常、モデルが 1 つの問題でうまく機能する場合、他の問題ではうまく機能しないはずであることを意味し、高度にカスタマイズされた仮定が求められる。
しかし、ディープラーニングの発展は、この常識とはまったく逆の方向に進んでいる。我々は、手作業による特徴エンジニアリング (SWIFT、HOG など) から、特定のドメインに特化したニューラル ネットワーク (視覚用の CNN、シーケンス用の RNN、表形式データ用の MLP など)、そしてあらゆるものに対応するトランスフォーマーへと、さまざまなモデルの融合を目の当たりにしてきた。この結果は、ニューラル ネットワーク モデルと、自然発生データの分布 (均一にサンプリングされたデータではなく) の両方によって説明でき、コルモゴロフ複雑度が低くなるというバイアスがある。驚くべきことに、画像認識用の畳み込みニューラル ネットワークなど、特定のドメイン向けに設計されたモデルでさえ、このバイアスのために、表形式データなどのまったく異なるデータ モダリティに対して帰納バイアスがあることが証明されている (Goldblum ら、2024)。1つの問題でトレーニングされたニューラル ネットワークから始めて、コルモゴロフ複雑度の上限を設定することで、他の問題や他のモダリティでのパフォーマンスに関する空虚でない汎化境界を導き出すことができる。
実際、コンテキスト内学習、つまりモデルがパラメータを更新せずに学習する機能は、ニューラル ネットワークでは非常にうまく機能する。ある意味では、多くの従来のモデルもコンテキスト内学習、またはそれに近いものを実行している。つまり、固定 RBF カーネルでガウス過程を使用し、トレーニング データで条件付けしてから事後予測をサンプリングすると、モデル表現を更新せずに条件付き生成が行われる。ただし、トランスフォーマーのコンテキスト内学習の相対的な普遍性は前例のないものである。たとえば、テキスト補完で事前トレーニングされた標準的な LLM は、時系列データでトレーニングされた専用の時系列モデルと比較して、驚くほど競争力のあるゼロショット時系列予測を行うことができる! (Gruver 他、2024)。
言い換えれば、ニューラル ネットワークはデータの豊富な表現を学習するだけでなく、他のモデル クラスと比較して、現実世界の問題全体で比較的普遍的な表現を学習する。コンテキスト内学習では、これらは固定された表現ではないことを強調する。事前トレーニング中に、トランスフォーマーは学習することを学習し、オッカムの剃刀などの帰納原理を発見する (Gruver 他、2024 年、Goldblum 他、2024 年)。GP の例えでは、事前トレーニング済みのトランスフォーマーは、さまざまなカーネルを持つ GP エキスパートの大規模な混合物と考えることができる。下流のデータセットに基づいて、トランスフォーマーは事前トレーニングで見たものに基づいて、適切なカーネルの組み合わせを選択する。
モード接続は、ニューラル ネットワークとは比較的異なる驚くべき現象である (Garipov 他、2018 年、Draxler 他、2018 年、Frankle 他、2020 年、Freeman と Bruna、2017 年、Adilova 他、2023 年)。ニューラル ネットワークを異なる初期化で複数回再トレーニングすると、その間に大きな損失障壁がある孤立した局所最適解に収束すると考えられていた。しかし、図 7 に示すように、これらの異なる解の間には、トレーニング損失が基本的にゼロのままである単純なパスがあることが判明した (Garipov 他、2018 年、Draxler 他、2018 年)。言い換えれば、収束した解を局所最適解と呼ぶこと自体が誤りである。重要なのは、モード接続曲線に沿ったパラメータ設定が、パラメータの対称性などのモデル仕様の退化を表すのではなく、テストポイントで異なる予測を行う異なる関数に対応していることである。
モード接続は、ディープラーニングにおける汎化の理解に深い影響を与える。実際、歴史的にディープラーニングに対する最も一般的な反論の 1 つは、損失ランドスケープ (トレーニング目標) の極端なマルチモーダル性である。モード接続は、実際に見つけている解がすべて相互に関連していることを示している。したがって、モード接続を理解し、この現象に触発された実用的な手順を開発することは、活発な研究分野となっている (例: Kuditipudi 他、2019 年、Frankle 他、2020 年、Benton 他、2021 年、Zhao 他、2020 年、Ainsworth 他、2022 年)。
モード接続は、確率的重み平均化 (SWA) (Izmailov 他、2018) などの一般的な最適化手順にも影響を与え、それがモデルスープ (Wortsman 他、2022) やモデルマージの領域 (Ainsworth 他、2022、Yang 他、2024) に影響を与えた。
しかし、表現学習と同様に、モード接続性はニューラル ネットワークに完全に固有のものではない (例: Kanoh & Sugiyama、2024)。ただし、モード接続性は主にディープラーニングの現象であり、明らかに洗練された非凸損失ランドスケープにのみ適用できる。
過剰パラメータ化、良性過剰適合、および二重降下は、(さらなる)研究に値する興味深い現象である。しかし、広く信じられていることとは反対に、これらは汎化を理解するための長年の枠組みと一致しており、他のモデルクラスを使用して再現可能であり、直感的に理解できる。今後、さまざまなコミュニティをより緊密に結び付け、さまざまな視点や一般化フレームワークが見落とされるリスクを軽減できるよう支援できればと考えている。
グロッキングとスケーリングの法則は、最近注目されている他の現象であり、同様に興味深く、さらに理解する価値がある。しかし、この論文で検討する現象とは異なり、これらは、汎化フレームワークを再考する必要がある証拠として、またはディープラーニングの現象として提示されることは通常ない。 そして実際、スケーリングの法則とグロッキングは線形モデルに適用されることが示されている (Linら, 2024; Atanasovら., 2024; Millerら., 2023; Leviら, 2023)。重要なのは、図 2 で見たように、PAC-Bayes と可算仮説の境界も大規模な LLM と一致しており、最近の研究では、これらの境界がChinchillaスケーリングの法則を記述していることが示されている (Finzi et al., 2025)。
ディープラーニングの汎化におけるオプティマイザーの役割は何か?図 6 の緑色とピンク色は基本的に反転しており、ディープラーニングが機能する主な理由は、確率的オプティマイザーの暗黙のバイアスにより、汎化の優れた低損失解の比較的小さなサブスペースを横断するためであるという通説がある。ただし、完全なバッチ勾配降下法だけでなく、損失がしきい値を下回ったときに停止する推測と確認でも、確率的最適化と同様の汎化を備えた解を見つけることができることが示されている (Geiping 他、2021 年、Chiang 他、2022 年)。これは、図 6 (右) と一致している。原理的には、このような損失ランドスケープの下でオプティマイザーが依然として悪い最適値を見つけることは可能であるが、積極的に敵対的である必要がある。敵対的とはほど遠い、確率的最適化には、確かに汎化を改善できるバイアスがある。しかし、重要なのは、これらのバイアスは、妥当な汎化には必要ないということである。もちろん、確率的最適化は、他の方法よりも計算上はるかに実用的です。推測と検証を使うことを提案している人はいない。さらに、与えられた計算予算内でより汎化できる最適化装置を開発することは、特に最近の結果が2次最適化装置の台頭を示していることから、特に刺激的な研究方向である(Liuら、2025; Vyasら、2024)。最後に、セクション3.1の汎化境界は、モデルが確率的最適化を使用するかどうかに関係なく評価でき、実際、これらの境界は、ベイズ推論を実行するガウス過程の良性過剰適合動作を追跡する。
構造リスク最小化とソフトな帰納バイアスの関係はどのようなものだろうか?SRM (構造リスク最小化)はソフトな帰納バイアスをエンコードする方法あるが、焦点が狭く、動機も異なることがよくある。SRM は、データの適合とモデルの複雑さをトレードオフして、VC 次元を削減するメカニズムとしてよく使用される。SRM は通常、任意の柔軟なモデルの処方箋として使用されることはない。実際、標準の ℓ2 正則化に対応する事前分布を持つモデル選択ツールは、中間次数モデルを使用する必要があることを示唆している (Bishop、2006)。我々の論文の重要なポイントは、データに完全に適合するモデル (ノイズを含む) を採用できるが、それでも単純さへのバイアスがあるということである。ソフトな帰納バイアスを実装する他の方法には、オーバーパラメータ化、ベイズ事前分布と周辺化、オプティマイザー、アーキテクチャ仕様などがある。
ディープラーニングの汎化をよりよく理解するにはどうすればよいか?ディープラーニングの汎化には、多くの興味深い未解決の問題がある。アプローチとして、ニューラル ネットワークが実際に到達する解を分析して、その動作を説明することが有望であると考えている。セクション 3.1 の汎化境界は完全に経験的であり、非漸近的であり、単一のサンプルを使用して評価できる。経験的に境界を評価できることは、経験的モデルの動作のどれだけが理論によって実際に説明されるかを判断する上で不可欠であると考えている。ソロモノフ事前分布は、記述的一般化境界の評価に特に役立つことがわかった。ソロモノフ帰納法では、考えられるすべてのプログラムを含む最大限にオーバーパラメータ化されたモデルを使用するが、短いプログラムに指数関数的に高い重みを割り当てる理想的な学習システムを形式化する。将来的には、より狭い境界につながる可能性のある事前分布の特性を調査し、ディープラーニングの汎化をさらに厳密に説明することは有益であろう。
有益な議論をしてくれたShikai Qiu, Pavel Izmailov,Marc Finzi, Gautam Kamath, Micah Goldblum, Alan Amin, Jacob Andreas, Alex Alemi, Lucas Beyer, Mikhail Belkin, Sanae Lotfi, Martin Marek, Sanyam Kapoor, Patrick Lopatto, Preetum Nakkiran, Thomas Dietterich, and Sadhika Malladi に感謝する。本研究の一部はNSF CAREER IIS-2145492, NSF CDS&EMSS 2134216, NSF HDR-2118310, BigHat Biosciences, Capital One, Amazon Research Award によってサポートされた。
PACBayes と可算仮説境界については、よくある誤解がいくつかある。
誤解: PAC-Bayes は、事後サンプルの予想される一般化を特徴付けるため、実際に使用する決定論的にトレーニングされたネットワークではなく、確率的ネットワークにのみ適用される。ただし、事後確率はベイズ事後確率である必要はなく、点質点事後確率と離散仮説空間を使用して PAC-ベイズ境界を評価できる。KL ダイバージェンスの相対エントロピー定義 \(\mathbb K\mathbb L(Q ‖ P) = \mathbb H(Q, P) − \mathbb H(Q)\) を使用すると、クロスエントロピー \(\mathbb H(Q, P)\) は \(\log_2\frac{1}{P(h)}\) になり、エントロピー \(\mathbb H(Q)\) または点質点 \(Q\) からのサンプルを見る際の「驚き」はゼロになり、可算仮説境界に非常によく似た境界が回復されます。あるいは、可算仮説境界は、決定論的にトレーニングされたモデルに直接適用される。
誤解: 可算仮説の境界は、連続パラメータを持つモデルには適用されない。我々が使用するニューラル ネットワークは実際にはコンピュータ上のプログラムであるため、有限の仮説空間を表す必要がある。重みは、浮動小数点などの精度によって決定される有限の数の値しか取ることができない。浮動小数点ニューラル ネットワーク パラメータ値によって表される仮説が多数あるため、可算仮説の境界は緩いものでなければならないという、関連する誤解がある。ただし、境界の形式から、仮説の数を厳密に測定することは避け、代わりにどの仮説が事前に可能性が高いかという観点から一般化を理解する必要があることがわかる。実際、これらの境界は、より多くの仮説を表す大規模なモデルではより厳しくなる可能性がある (Lotfi ら、2024a)。
誤解: パラメータの数が増えると、これらの境界は緩くなる。一部の PAC-Bayes 境界を含む多くの境界にはパラメータカウント項があるが (Jiang ら、2019)、これはすべての PAC-Bayes 境界または可算仮説境界に当てはまるわけではない。実際、最近の境界はモデルパラメータの数が増えると厳しくなる可能性がある (Lotfi ら、2022a、2024a、b)。これは、モデルが大きいほど圧縮バイアスが強くなり、境界の複雑性ペナルティが減少する可能性があるためである。
誤解: ニューラル ネットワークの境界が狭いのは、非現実的なモデル圧縮のためである。圧縮境界と呼ばれる形式の境界があり、これは、パラメータが低次元空間に圧縮されたモデルの一般化を制限する。このアプローチは、大規模なデータセットで大規模なニューラル ネットワークの非空境界を達成することに初期段階で成功したのは事実である (Zhou 他、2018 年、Lotfi 他、2022a)。ただし、対処すべき誤解がいくつかある。(1) パラメータ空間の線形サブスペースの形成などの圧縮手法は、元のモデルとほぼ同じパフォーマンスを示すことがよく知られている (Li 他、2018 年)。境界は、非現実的なモデル削減ではなく、実際に説得力のあるモデルを記述することがよくある。(2) 大規模なニューラル ネットワークを低次元サブスペースに圧縮する機能は、汎化に関する情報を提供する。(3)最近の非空境界は、Lotfi et al.(2024b)やFinzi et al.(2025)における10億パラメータLLMの境界のような圧縮境界ではない。
誤解: コルモゴロフ複雑度は計算不可能であるため、ソロモンオフ事前分布に基づく一般化境界は評価できない。プレフィックスのないコルモゴロフ複雑度 \(K(h)\) は、事前に指定されたコーディングを使用して \(h\) を表すビット単位の最短プログラムを表す。最短プログラムを計算することはできないが、モデルの保存ファイルサイズと、モデルの読み込みと実行に使用する (Python などの) スクリプトのサイズなど、データに依存しない項によって与えられる定数によって、最短プログラムの上限を設定することはできる。\(K(h|A)\) を操作することで、A で表されるデータに依存しないこれらの定数項をソロモンオフ事前分布に吸収できる。次に、非プレフィックスフリー(標準)コルモゴロフ複雑度 \(C\)(\(A\) を条件とする)をトレーニング済みモデルの保存ファイルサイズで上限設定し、有益な汎化境界を計算できる。
ちなみに、コルモゴロフ複雑度の重要な特性は、使用されるプログラミング言語やユニバーサル チューリング マシンとは無関係に絶対情報を測定することである。特定の文字列を参照せずに、ある言語のコードを別の言語に変換するコンパイラを作成できる。特に、不変性定理により、任意の 2 つのユニバーサル チューリング マシンにおけるコルモゴロフ複雑度の差は、可能な限り短いコンパイラによって上限が設定される (Kolmogorov、1965 年、Li & Vit´anyi、2008 年)。このようなコンパイラは通常、最大でキロバイトのオーダーで、テラバイトになることもある一般的な ML データセットと比較すると無視できるほど小さいものである。
誤解: 境界は、事前分布 P(h) が誤って指定されていない場合にのみ適用される。境界では、事前分布が正しい仮説を生成するために使用されることや、仮説が含まれること、さらには境界を設定するモデルによって使用されることさえ要求されない。境界は、境界を計算するメカニズムを提供するだけである。たとえば、境界で使用される事前分布が単純な解を優先し、モデルの事前分布が複雑な解を優先する場合、境界は緩くなる。境界の仮定は、実際に使用しているモデルに適用される。これには、たとえば、Zhang ら (2016) の CIFAR 良性オーバーフィッティング実験が含まれる。
Rademacher 複雑度 (Bartlett & Mendelson、2002) は、モデルが均一な \(\{+1,−1\}\) ランダム ノイズに適合する能力を正確に測定する。特に、仮説空間 \(\mathcal H\) と入力サンプル \(\{x_i, . . , x_n\}\) の Rademacher 複雑度は \(\mathcal R(\mathcal H) = \mathbb E_σ[ sup_{h∈\mathcal H}\frac{1}{n}\sum_{i=1}^nσ_ih(x_i)]\) である。ここで \(σ_i\) は i.i.d. Rademacher ランダム変数 (等確率の \(\{+1,−1\}\)) である。仮説 h の期待リスクは、\(R(h) ≤ \hat R(h) + 2\mathcal R(\mathcal H) + C\) として制限される。ここで、\(C\) は損失関数 \(n\) と、制限の信頼度 \(1 − δ\) によって定義される定数である。したがって、モデルに Rademacher ノイズに適合できる仮説空間 H がある場合、Rademacher 一般化制限は有益ではない。
同様に、VC 次元 (Vapnik ら、1994) は、仮説空間 \(mathcal H\) が \(\{+1,−1\}\) ラベルを持つ d 点の任意の集合に適合 (「粉砕」) できる最大の整数 d を測定する (たとえば、これらの点をすべての \(2^d\) 可能な方法で分類する)。VC 次元 \(\mathcal H\) が \(d\) の場合、予想される一般化誤差は \(R(h) ≤ \hat R (h) + O\Big(\sqrt{\frac{d\log(n)}{n}}\Big)\) として制限される。したがって、仮説空間が大きいモデルには、情報のない VC 一般化境界がある。
脂肪粉砕次元 (Alon et al., 1997) \(fat_γ(\mathcal H)\)は、VC 次元を、あるマージン \(γ\) (または、各ターゲット \(y_i\) に対して、ある範囲 \([y_i − γ, y_i + γ]\) 内のすべての可能な値を持つ関数) でフィッティング (「粉砕」) ラベルに調整する。脂肪粉砕次元は、Rademacher 複雑度と密接に関連している: \(\mathcal R(\mathcal H) ≤ cγ\sqrt{\frac{fat_γ(\mathcal H)} {n}}\)。期待される一般化は、\(R(h) ≤ \hat R(h) + O\Big(\sqrt{\frac{fat_γ(\mathcal H)\log(n)}{n}}\) と制限できる。\(γ\) が大きいほど、制約を満たすのが難しくなるため、脂肪粉砕次元 \(d\) は減少する。モデルが小さい \(γ\) でのみノイズを適合できるが、大きい \(γ\) では適合できない場合、ノイズを適合する能力と柔軟な仮説空間は脂肪粉砕次元によって説明できる。ただし、脂肪粉砕次元は、一般に任意のニューラル ネットワークに対して計算するのが困難である。
表 1 に、さまざまな一般化境界の比較概要を示す。
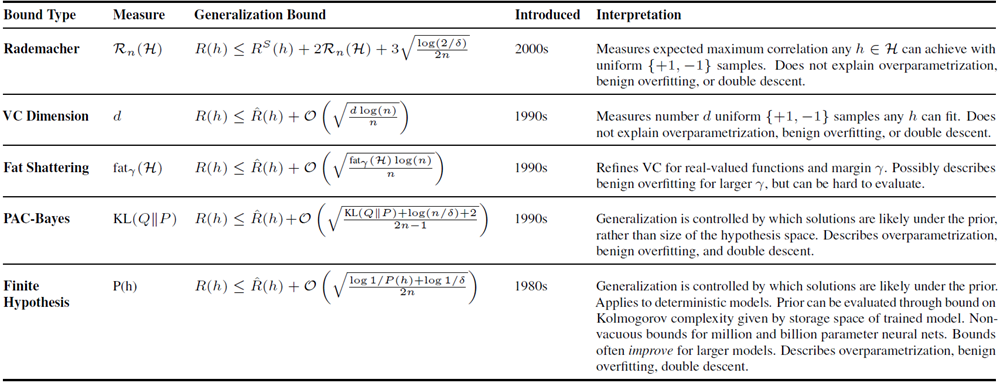
表1. 汎化境界のまとめ
定理 C.1. 制限されたリスク \(R(h, x_i) ∈ [a, a +Δ]\) と、\(\{x_i\}\) に依存しない事前確率 \(P(h)\) を持つ可算な仮説空間 \(h ∈ \mathcal H\) を考る。経験的リスク \(\hat R(h) = \frac{1}{n}\sum_{i=1}^n R(h, x_i)\) を、固定された仮説 h に対する独立したランダム変数 \(R(h, x_i)\) の合計とする。期待リスクを \(R(h) = \mathbb E[\hat R(h)]\) とする。
少なくとも\(1 − δ\)の確率で: \[ R(h)\leq\hat R(h)+\Delta\sqrt{\frac{\log 1/P(h)+\log 1/\delta}{2m}} \tag{5} \]
証明 (Lotfi et al., 2024a)。\(m\hat R(h)\) は独立かつ有界なランダム変数の合計なので、与えられた \(h\) の選択に対して Hoeffding の不等式 (Hoeffding, 1994) を適用できる。任意の \(t > 0\) に対して
\[ \begin{align} &P(R(h)\geq\hat R(h)+t)=P(nR(h)\geq n\hat R(h)+nt) \\ &P(R(h)\geq\hat R(h)+t)\leq\exp(-2nt^2/\Delta^2) \end{align} \]それぞれの仮説hに応じてt(h)を異なる方法で選択する。 \[ \exp(-2nt(h)^2/\Delta^2)=P(h)\delta \]
\(t(h)\)を解くと、 \[ t(h)=\Delta\sqrt{\frac{\log 1/P(h)+\log 1/\delta}{2n}} \tag{6} \]
この境界は固定仮説 \(h\) に対して成り立つ。しかし、訓練データを用いて構築された\(h^∗(\{x\})\)に対しては、ランダム変数 \[ \hat R(h^*)=\frac{1}{n}\sum_{i=1}^n R(h^*(\{x\}),x_i) \]
は独立した確率変数の和として分解することはできない。\(h^∗ ∈ \mathcal H\) なので、任意の \(h\) に対して \(R(h) ≥ \hat R(h) + t(h)\) となる確率を制限できれば、その制限は \(h^∗\) に対しても成り立つ。
事象\(\bigcup_{h\in\mathcal H}[R(h)\geq\hat R(h)+t(h)]\)に和集合を適用すると、 \[ \begin{align} P(R(h^*)\geq\hat R(h^*)+t(h^*)) &\leq P\left(\bigcup_{h\in\mathcal H}[R(h)\geq\hat R(h)Lt(h)]\right)\\ \\ &\leq\sum_{h\in\mathcal H} P\left(R(h)\geq\hat R(h)Lt(h)\right)\\ \\ &\leq\sum_{h\in\mathcal H} P(h)\delta=\delta \end{align} \]
したがって、任意の \(h\)(\(x\)に依存するかどうか)に対して、少なくとも1 − δの確率で以下となる。 \[ R(h)\leq\hat R(h)+\Delta\sqrt{\frac{\log 1/P(h)+\log 1/\delta}{2n}} \]
図 1(a)(b)(c) では、次数依存の正則化 \(\sum_j 2^jw_j^2\) (緑) を伴う 150 次多項式を使用して、(a) \(\sin(x)\cos(x^2)\)、(b) \(x+\cos(x)\)、(c) \(\mathcal N(0, 1)\) ノイズから生成された回帰データを適合させている。
図 1(d)(e) は Wilson & Izmailov (2020) から引用したもので、RBF カーネルを使用したガウス過程、PreResNet-20 および等方事前分布 \(p(w) =\mathcal N(0, α^2I)\) およびラプラス周辺尤度を使用し、Zhang ら (2016) の CIFAR-10 ノイズ ラベル実験を再現している。
図 1(f) は Maddox ら (2020) から改変したもので、層幅が増加する ResNet-18 を使用して、トレーニング損失、テスト損失、および \(α = 1\) の有効次元を測定します。図 1(g) では、\(X_i = y_i + \epsilon\) の各列でランダム フィーチャ最小二乗モデル \(Xw = y\) を使用します (\(\epsilon ∼\mathcal N(0, 1)\))。MSE を測定し、有効次元には α = 1 を使用する。
図 2 は Lotfiら (2024a) から引用したもので、さまざまなサイズの LLM について、セクション 3 のコルモゴロフ複雑度の上限とともに可算仮説境界を評価している。
図 5 は、2 次多項式、15 次多項式、および \(\cos(\frac{3}{2}x)\) から生成されたデータに 2 つの 15 次多項式と 1 つの 2 次多項式を当てはめている。15 次多項式の 1 つは、次数依存の正則化 \(\sum_j 0.01^2j^2w_j^2\) を使用する。トレーニングおよびテストの入力位置は、\(\mathcal N(0, 1)\) からサンプリングされる。テスト サンプルの数は 100 で、トレーニング サンプルの数は 10 から 100 の範囲である。各トレーニング サンプル サイズについて、データを 100 回再生成し、RMSE とその標準偏差 (網掛けで表示) を記録する。同様の結果が Goldblum ら (2024) でも示されている。
その他の図はすべて概念図である。