AlphaEvolve

このホワイトペーパーでは、未解決の科学的問題への取り組みや計算インフラストラクチャの重要な部分の最適化など、非常に困難なタスクにおける最先端の LLM の機能を大幅に強化する進化的コーディングエージェントである AlphaEvolve を紹介します。AlphaEvolve は、コードに直接変更を加えることでアルゴリズムを改善する LLM の自律パイプラインを調整します。進化的アプローチを使用して、1 人以上の評価者から継続的にフィードバックを受け取りながら、AlphaEvolve はアルゴリズムを反復的に改善し、科学的および実用的な新たな発見につながる可能性があります。私たちはこのアプローチをいくつかの重要な計算問題に適用することで、その幅広い適用可能性を実証しています。Google の大規模計算スタックの重要なコンポーネントの最適化に適用されたとき、AlphaEvolve はデータセンター向けのより効率的なスケジューリングアルゴリズムを開発し、ハードウェアアクセラレータの回路設計において機能的に同等の簡素化を見つけ、AlphaEvolve 自体を支える LLM のトレーニングを加速しました。さらに、AlphaEvolveは、数学とコンピュータサイエンスの幅広い問題において最先端の解法を凌駕する、新しく証明可能な正解アルゴリズムを発見し、従来の自動発見手法の範囲を大幅に拡大しました（Romera-Paredes et al., 2023）。特に、AlphaEvolveは、2つの4×4複素数値行列を48回のスカラー乗算で乗算する手順を見つける探索アルゴリズムを開発しました。これは、この設定において、56年ぶりにStrassenのアルゴリズムを大幅に改善したことになります。私たちは、AlphaEvolveやそれに似たコーディングエージェントが、科学と計算の多くの分野における問題解決の改善に大きな影響を与えることができると信じています。

1. はじめに

新たな科学的発見や商業的に価値のあるアルゴリズムの開発など、価値の高い新しい知識の発見には、通常、アイデア創出、探索、見込みのない仮説の遡及、実験、検証という長期にわたるプロセスが必要です。近年、大規模言語モデル（LLM）を用いてこのプロセスの重要な部分を自動化することに大きな関心が寄せられています。ここでの成功への期待は、テスト時の計算を用いて能力を強化できる最近のLLMの驚異的な能力[31, 73]と、言語生成とアクションを組み合わせたエージェントの台頭[85, 111]によって牽引されています。これらの進歩は、確立された様々なベンチマークにわたってパフォーマンスを向上させ、仮説生成[33]や実験設計[7, 42]などの発見指向のタスクを加速しました。しかし、LLMパイプラインを全く新しい科学的または実用的な発見にまで至らせることは、依然として困難です。

このホワイトペーパーでは、進化的計算とLLMベースのコード生成を組み合わせてこの課題に取り組む、LLMコード超最適化エージェント「AlphaEvolve」を紹介します。AlphaEvolveは、発見候補を自動的に評価できる幅広い科学的および工学的発見問題に焦点を当てています。AlphaEvolveは、発見候補（新しい数学的オブジェクトや実用的なヒューリスティックなど）をアルゴリズムとして表現し、一連のLLMを使用してそのようなアルゴリズムのプールを生成、評価、進化させます。LLM指向の進化プロセスは、コード実行と自動評価に基づいています。この評価メカニズムにより、AlphaEvolveはベースとなるLLM [43]からの誤った提案を回避することができます。

AlphaEvolveにおける進化プロセスは、現代のLLMのフィードバック応答能力を活用し、構文と機能において初期の候補プールとは大きく異なる候補の発見を可能にする。これは、新しいアルゴリズムの発見が本質的な目標である問題だけでなく、関心のある解がアルゴリズムそのものではなく、その解がどのように構築または発見されるかをアルゴリズムが記述できる幅広い問題にも適用できる。後者の場合、アルゴリズムの発見は単なる手段的な目標に過ぎないが、解を直接探索するよりも驚くほど効果的な戦略であることが判明している[80]。

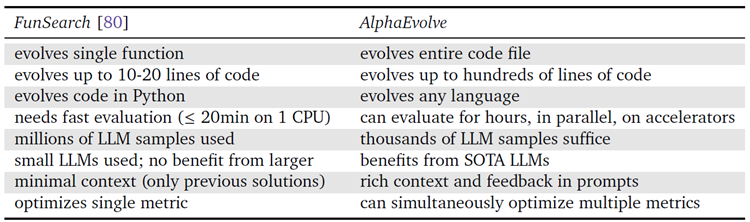
進化的手法とコーディングLLMを組み合わせるというアイデアは、これまで様々な専門的な設定で検討されてきました。特に、AlphaEvolveはFunSearch [80]（表1を参照）の大幅な強化版です。FunSearchは、LLM誘導進化を用いてヒューリスティックを発見し、新しい数学的オブジェクトを構築したり、オンラインアルゴリズムの動作を駆動したりしていました。また、関連するアプローチは、シミュレーションロボットのポリシー発見[55]、シンボリック回帰[34, 86]、組み合わせ最適化のためのヒューリスティック関数の合成[61]などのタスクで使用されています。これらのシステムとは対照的に、AlphaEvolveは最先端の（SOTA）LLMを活用して、複数の関数とコンポーネントにまたがる複雑なアルゴリズムを実装する大規模なコードを進化させます。その結果、規模と一般性において先行システムを大幅に上回ることができます。

表 1 | AlphaEvolve と以前のエージェントの機能と一般的な動作。

自動評価指標の使用はAlphaEvolveにとって大きな利点となる一方で、同時に制約も伴います。特に、手動による実験を必要とするタスクはAlphaEvolveの適用範囲外となります。数学、コンピュータサイエンス、システム最適化といった分野では、自動評価指標の使用が一般的に許容されるため、AlphaEvolveにおける私たちの取り組みはこれらの分野に重点を置いています。具体的には、アルゴリズム設計と構成数学におけるいくつかのよく知られた未解決問題、そしてGoogleの大規模計算スタックにおける重要なレイヤーの最適化の進展にAlphaEvolveを活用しています。

アルゴリズム設計においては、行列乗算のための高速アルゴリズムを発見するという根本的な問題を考慮します。この問題には、以前より特化したAIアプローチが適用されてきました[25]。汎用性が高いにもかかわらず、AlphaEvolveは[25]を凌駕し、14種類の行列乗算アルゴリズムのSOTAを改善しました。特に、4×4行列の場合、AlphaEvolveはStrassen (1969)のアルゴリズムを改良し、4×4複素数値行列を48回の乗算で乗算するアルゴリズムを発見しました²

² 発見されたアルゴリズムとその他の新しい数学的結果は、https://colab.research.google.com/github/google-deepmind/alphaevolve_results/blob/master/mathematical_results.ipyn でご覧いただけます。

数学では、与えられた数学的定義に従って、これまで知られているすべての構成よりも優れた特性を持つ構成（オブジェクト）を発見することで進歩できる、幅広い未解決問題を考察します。私たちは、そのような問題の多数（50以上）にAlphaEvolveを適用し、それらの約75％で既知の最良の構成と一致しました（多くの場合、これらの構成は既に最適である可能性があります）。約20％の問題では、AlphaEvolveはSOTAを上回り、新しい、証明可能に優れた構成を発見します。これには、エルデシュ[24]によって設定された最小オーバーラップ問題の改善と、11次元のキッシング数問題[8, 30]の改善された構成が含まれます。

最後に、Google のコンピューティングスタックの異なるレイヤーにまたがる 4 つのエンジニアリング問題に AlphaEvolve を適用しました。具体的には、Google のクラスタ管理システムのスケジューリングヒューリスティックの発見、LLM のトレーニングに使用される行列乗算カーネルの最適化、TPU 内で使用される演算回路の最適化、そして Transformer におけるアテンションの実行時間の最適化です。これらのコンポーネントは長期間にわたって繰り返し実行されるため、改善点は非常に貴重です。

2. AlphaEvolve

AlphaEvolveは、LLMへのクエリを含む計算の自律パイプラインをオーケストレーションし、ユーザーが指定したタスクに対応するアルゴリズムを生成するコーディングエージェントです。オーケストレーション手順は、タスクに関連付けられた自動評価指標のスコアを向上させるプログラムを段階的に開発する進化的アルゴリズムです。図1はAlphaEvolveの概要を示し、図2は拡大図を示しています。

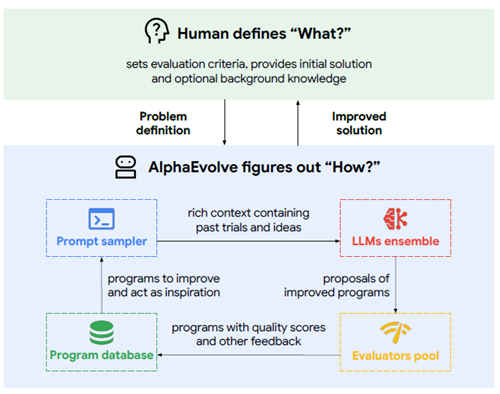
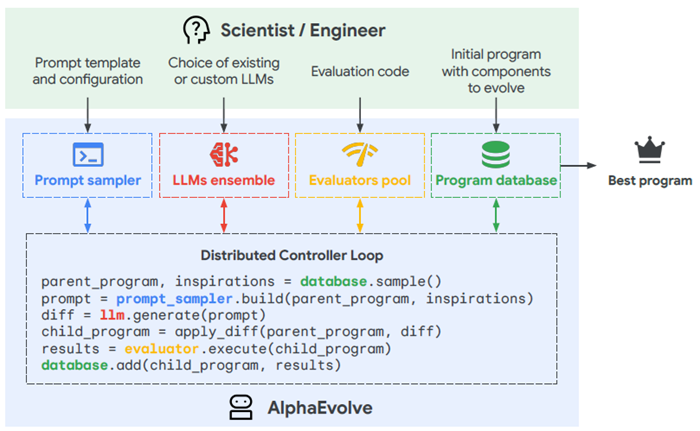
図2 | AlphaEvolveの発見プロセスの拡大図。ユーザーは、初期プログラム（進化させるコンポーネントがマークされている）、評価コード、およびオプションの設定を提供します（セクション2.1）。AlphaEvolveは進化ループを開始します。プロンプトサンプラーは、プログラムデータベースのプログラムを使用して、豊富なプロンプトを構築します（セクション2.2）。これらのプロンプトに基づいて、LLMはコード変更（difs）を生成し、それに基づいて新しいプログラムを作成します（セクション2.3）。その後、評価者によってスコアが付けられ（セクション2.4）、有望な解がプログラムデータベースに登録されます（セクション2.5）。これにより、より優れたプログラムの反復的な発見が促進されます。

2.1. タスクの仕様

評価。AlphaEvolveは機械で評価可能な解を扱う問題を扱うため、ユーザーは生成された解を自動的に評価するメカニズムを提供する必要があります。このメカニズムは、解をスカラー評価指標の集合にマッピングする関数ℎの形をとります。慣例的に、これらの指標は最大化されます。現在の設定では、ℎは通常、evaluateと呼ばれるPython関数として実装され、固定された入出力シグネチャを持ち、スカラーの辞書を返します。

アプリケーションによっては、この関数の実行に1台のデバイスで数秒しかかからない場合もあれば、膨大な計算が必要となる場合もあります。数学の問題の場合、関数ℎは通常非常に単純です。例えば、特定のプロパティを満たす可能な限り最大のグラフを見つけたい場合、関数ℎは進化型コードを呼び出してグラフを生成し、プロパティが成立するかどうかを確認し、グラフのサイズをスコアとして返します。より複雑なケースでは、関数ℎは進化型検索アルゴリズムの実行や、機械学習モデルのトレーニングと評価を伴う場合があります。

API. 　コードベース全体にわたる複数のコンポーネントの進化をサポートするため、AlphaEvolve は入力 API を公開しています。この API では、コードブロックにシステムによって進化するコードブロックとして注釈を付けることができます。図 3a を参照してください。この設計により、特別なマーカー (# EVOLVE-BLOCK-START および # EVOLVE-BLOCK-END) をコードにコメントとして追加するだけで、最小限の変更で既存のコードベースとの統合が容易になります。

このような進化ブロック内のユーザー提供コードは、AlphaEvolveによって改良される初期ソリューションとして機能し、残りのコードは進化した部分を結び付けるスケルトンを形成し、evaluateから呼び出せるようにします。この初期実装は完全である必要がありますが、例えば適切な型の定数を返す1行の関数で構成されるなど、初歩的なものでも構いません。

　抽象化を選択する際の柔軟性。 AlphaEvolveは、同じ問題に非常に異なる方法で適用できます。特に、進化したプログラムが最終出力ではなく、解決策を発見するための手段である場合に有効です。たとえば、AlphaEvolveは、生の文字列表現で解決策を進化させたり（古典的な進化アルゴリズムのように）、解決策をゼロから構築する方法を指定する定義済みの形式の関数を進化させたり（[80]で採用されているアプローチ）、固定された計算予算内で解決策を見つけるための特注の検索アルゴリズムを進化させたり、中間解決策と検索アルゴリズムを一緒に共進化させて、各検索アルゴリズムが特定の中間解決策をさらに改善するように特別に調整されるようにすることができます。

問題によって抽象化のレベルが異なると、より効果的に機能することがわかりました。例えば、対称性の高い解を持つ問題では、コンストラクタ関数を進化させる方が有利です。これは、コンストラクタ関数の方が簡潔になる傾向があるためです[80]。一方、非対称な解を持つ問題では、カスタマイズされた探索アルゴリズムを進化させる方が効果的です。

2.2. プロンプトサンプリング

AlphaEvolveはSOTA LLMを活用しているため、様々なカスタマイズをサポートし、主要な進化プロンプトの一部として長いコンテキストを提供します。このプロンプトは、プログラムデータベースから抽出された複数の既知解と、特定の解への変更を提案する方法に関するシステム指示で構成されています。これらの主要な要素に加えて、ユーザーは以下のように様々な方法でプロンプトを自身のニーズに合わせてさらにカスタマイズできます。

2.3. 創造的な生成

AlphaEvolveは進化的プロセスを推進するために、SOTA LLMの機能を活用します。SOTA LLMの主な役割は、以前に開発されたソリューションに関する情報を消化し、ソリューションを改善するための新しい多様な方法を提案することです。AlphaEvolveはモデルに依存しませんが、アブレーションにおいては、基盤となるLLMの性能が向上するにつれてAlphaEvolveのパフォーマンスが向上することが観察されています（セクション4を参照）。

図3 | AlphaEvolveを教師あり学習パイプラインの進化に適用する例。すべてのスニペットは省略形で示されており、省略記号(...)はスキップされた行を示しています。(a) 進化対象としてマークされたブロックを含むユーザー提供ファイルと、現在のバージョンのコードにスコアを付けるために呼び出すことができる特別なevaluate関数。(b) LLMに提供されるアセンブルされたプロンプトの例。(c) LLMによって生成される出力例。(c)で提案された差分は、プロンプト(b)に表示されている「現在のプログラム」に適用され、結果として得られた修正済みプログラムは評価者に送信されます。評価者は、(a)の評価関数を呼び出して、新しく提案されたプログラムのスコアを取得します。

出力形式 　AlphaEvolve が LLM に既存のコード (特に大規模なコードベース内) の変更を要求する場合、変更内容を特定の形式で一連の dif ブロックとして提供するよう要求します。

<<<<<<< SEARCH # Original code block to be found and replaced ======= # New code block to replace the original >>>>>>> REPLACE

ここで、<<<<<<< SEARCH と ======= の間にあるコードは、現在のプログラムバージョンで一致する正確なセグメントです。======= と >>>>>>> REPLACE の間にあるコードは、元のセグメントを置き換える新しいセグメントです。これにより、コードの特定の部分のみを対象的に更新できます。

進化するコードが非常に短い場合、または小さな変更よりも完全な書き換えの方が適切な場合は、dif 形式を使用するのではなく、LLM にコードブロック全体を直接出力するように指示するように AlphaEvolve を構成できます。

使用モデル AlphaEvolveは、大規模な言語モデルのアンサンブルを採用しています。具体的には、Gemini 2.0 FlashとGemini 2.0 Proを組み合わせて使用しています。このアンサンブルアプローチにより、計算スループットと生成されるソリューションの品質のバランスをとることができます。レイテンシが低いGemini 2.0 Flashは候補生成速度を向上させ、単位時間あたりに探索されるアイデアの数を増加させます。同時に、より優れた機能を持つGemini 2.0 Proは、進化的探索を大幅に前進させ、ブレークスルーにつながる可能性のある、高品質の提案を随時提供します。この戦略的な組み合わせにより、評価されるアイデアの量を最大化すると同時に、より強力なモデルによってもたらされる大幅な改善の可能性を維持しながら、全体的な発見プロセスを最適化します。

2.4. 評価

AlphaEvolveの進捗状況を追跡し、将来の世代に伝播させるアイデアを選択するために、LLMによって提案された新しいソリューションはそれぞれ自動的に評価されます。原理的には、このプロセスは、生成されたソリューションに対してユーザーが指定した評価関数ℎを実行するだけです。実際には、AlphaEvolveは、この評価をより柔軟かつ効率的にするためのオプションのメカニズムをサポートしています。

複数のスコア。 AlphaEvolve は、ユーザーが指定した複数のスコアの最適化、つまり 1 つまたは複数の評価基準で高いスコアを達成するオブジェクトを進化させることができます。これには、本質的な価値と手段的な価値の両方があります。複数のアプリケーションでは、複数の評価基準に対応するソリューション (またはそれらすべてに同時に強い 1 つのソリューション) の開発に真剣に取り組んでいますが、1 つのメトリックが特に興味深い場合でも、複数のメトリックを最適化すると、単一のターゲットメトリックの結果が改善されることがよくあります。これは、異なる評価基準で優れているプログラムは、多くの場合、明確な構造やロジックを持っているためです。これらの多様で高性能なプログラムの例 (それぞれが異なる「良い」の定義を表す) を言語モデルに提供されるプロンプトに組み込むことで、より多様な候補ソリューションの生成を刺激し、ターゲットメトリックに非常に効果的な新しいアプローチを発見する可能性が高まります。

2.5. 進化

AlphaEvolveは進化過程において、評価結果（スコアとプログラム出力）が付与された解を継続的に生成し、その数は増加していきます。これらの解は進化データベースに保存されます。進化データベースの主な目的は、過去に探索されたアイデアを将来の世代で最適に再浮上させることです。このようなデータベースを設計する際の重要な課題は、探索と活用のバランスを取り、多様性を維持しながら最良のプログラムを継続的に改善し、探索空間全体の探索を促進することです。AlphaEvolveの進化データベースは、MAPエリートアルゴリズム[71]と島型集団モデル[80, 94]を組み合わせたアルゴリズムを実装しています。

2.6. 分散パイプライン

AlphaEvolveは、非同期計算パイプライン（Pythonライブラリ asyncio を使用）として実装されています。このパイプラインでは、多数の計算が同時に実行されます。各計算は、次のステップが別の未完了の計算の結果に依存するたびにブロック（待機）されます。具体的には、非同期パイプラインはコントローラ、LLMサンプラー、および評価ノードで構成されます。パイプライン全体は、特定の計算速度ではなくスループットに最適化されており、特定の計算予算内で提案および評価できるアイデアの数を最大化します。

3. 結果

3.1. テンソル分解のための新しいアルゴリズムの発見による行列乗算の高速化

機械学習の計算を高速化することからリアルなコンピュータグラフィックスを可能にすることまで、行列の乗算はコンピュータサイエンスにおける数多くの重要なアルゴリズムとアプリケーションを支える基本的な演算として機能します。 Strassen [92] の先駆的な研究以来、2つの行列を乗算する任意のアルゴリズムは、特定の3Dテンソルをランク1テンソルに分解して表現できることが知られています。分解のランク（項の数）は、行列積を計算するために必要なスカラー乗算の数を正確に指定します。したがって、より高速な行列乗算アルゴリズムを開発するには、特定のテンソルの低ランク分解を見つける必要があります。この問題には、専用の交代最小二乗ソルバー [90] から深層強化学習 [25] やカスタム検索アルゴリズム [46] まで、多くのアプローチで取り組まれてきました。しかし、数十年にわたる努力にもかかわらず、2つの3×3行列を乗算するという単純なケースでさえ、達成可能な最小ランクがわかっておらず、問題の難しさを示しています。

問題の説明と標準的な勾配ベースのアルゴリズム（初期化子、再構成損失関数、Adam 最適化装置 [48] を含む）から始めて、AlphaEvolve は既存のアプローチを上回る高度なテンソル分解アルゴリズムを開発できます。各進化プログラムを評価するには、行列乗算ターゲットのセットを選択し、セクション 2.4 で説明した評価カスケードを使用して複数のランダムシードで初期化されたアルゴリズムを実行します。次に、各ターゲットで達成された最高 (最低) ランクと、このランクを達成したシードの割合としてパフォーマンスが測定され、AlphaEvolve にヒルクライムを行うための信号が提供されます。分解の正確性を保証し、潜在的な数値エラーを回避するために、評価時に各要素を最も近い整数または最も近い半整数に丸めます。また、アルゴリズムが整数に近い解を生成するように、この要求を LLM のプロンプトに自然言語で含めます。

表 2 では、 AlphaEvolve が開発したさまざまなアルゴリズムが、14 種類の異なる行列乗算ターゲットの最先端技術を改善していることがわかります。特に、2 つの 4 × 4 行列の乗算では、Strassen [92] のアルゴリズムを再帰的に適用すると、乗算回数が 49 回のアルゴリズムが得られ、これは任意の体で機能します。2 つの要素を持つ体の乗算という非常に特殊なケースでは、Fawzi ら [25] が乗算回数が 47 回のアルゴリズムを見つけました。56 年もの間、標数 0 の任意の体で乗算回数が 49 回未満のアルゴリズムを設計することは未解決の問題でした。AlphaEvolve は、48 回の乗算を使用して 2 つの 4 × 4 複素数値行列の乗算を行うアルゴリズムを見つける最初の方法です。

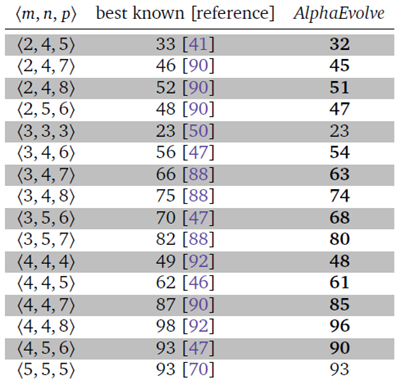
表2 | 𝑚 × 𝑛行列と𝑛 × 𝑝行列の積を計算するために必要なスカラー乗算回数の上限。これは、パラメーター ⟨𝑚, 𝑛, 𝑝⟩ を持つ対応する3Dテンソルの階数と同等です。ここに示した例以外にも、すべてのパラメーター 𝑚, 𝑛, 𝑝 ≤ 5 に対して、AlphaEvolve は既知の最良解と同等かそれを上回り、正確なアルゴリズムを提供しました（詳細な結果は付録の表3を参照）。⟨3, 4, 7⟩、⟨4, 4, 4⟩、および ⟨4, 4, 8⟩ の場合、AlphaEvolve によって発見されたアルゴリズムは、複素数値の乗算を使用しており、これは複素数値または実数値行列の正確な乗算に使用できます。この表に示されている分解は、付属のGoogle Colabで確認できます。

図4に示すように、AlphaEvolveは初期プログラムに大幅な変更を加え、より優れたアルゴリズムを設計するための独自のアイデアをいくつか導入しています。表2の結果の大部分（⟨4,4,4⟩を含む）は単純な初期プログラムから得られたものですが、一部のパラメータについては、初期プログラムに独自のアイデア（評価関数に確率性を追加したり、進化的アプローチを用いたりするなど）を加えることで、パフォーマンスをさらに向上させることができることがわかりました。これは、研究者とAlphaEvolveとの科学的コラボレーションの可能性を示唆しています。

3.2. 幅広い未解決数学問題に適した探索アルゴリズムの発見

数学研究における重要なフロンティアの一つは、ある尺度に基づいて最適、あるいはほぼ最適な特性を持つ物体や構成を発見することです。例としては、幾何学的形状の稠密充填[28]の発見から、特定の組合せ論的制約や解析的制約を満たす関数や集合の特定（例：[38, 39, 68, 101]）まで多岐にわたります。進歩は、既知の例をすべて凌駕する単一の構成を発見し、それによって最適値の新たな下限または上限を確立することに大きく依存しています。AlphaEvolveは、これらの問題に内在する広大な探索空間を探索するための強力なツールとして機能し、多様な未解決の数学的課題に効果的に取り組むことができることを実証します。

AlphaEvolveの能力を評価するため、解析学、組合せ論、数論、幾何学など、50以上の数学分野を網羅する厳選された数学問題セットにAlphaEvolveを適用し、様々なパラメータ設定（例えば、異なる次元やサイズ）で評価しました。AlphaEvolveは75%のケースで既知の最良の構成を再発見し、20%のケースでは、既知の最良の構成よりも優れた新しいオブジェクトを発見し、SOTAを改善しました。これらのケース全てにおいて、最初の出発点は単純な構成またはランダムな構成でした。これらの結果は、数学研究のための多用途ツールとしてのAlphaEvolveの幅広い可能性を裏付けています。

図4 | AlphaEvolveが提案した、より高速な行列乗算アルゴリズムを発見するための変更。差分全体は左側に概説されており（図9a～9cの拡大版を参照）、一部の抜粋は右側にハイライト表示されています。この例では、AlphaEvolveは、最適化と重みの初期化（右上）、損失関数（右中央）、ハイパーパラメータスイープ（右下）など、複数のコンポーネントにわたる広範な変更を提案しています。これらの変更は非常に重要であり、進化プロセス中に15回の突然変異を必要とします。

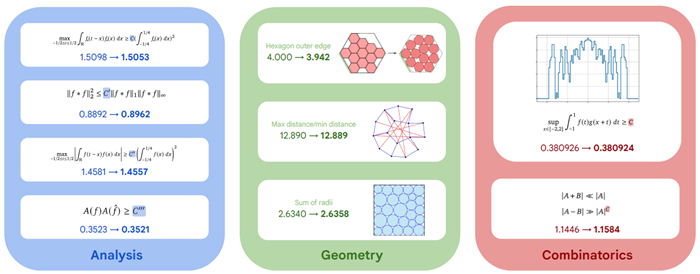
図5 | AlphaEvolveによって発見されたSOTAを破る数学的構成の例。AlphaEvolveの汎用性により、解析学（自己相関と不確実性不等式）、幾何学（パッキングと最小/最大距離問題）、組合せ論（エルデシュの最小重なり問題、有限集合の和と差）といった問題に取り組むことができます。

ここで使用されているAlphaEvolve構成の大きな利点は、その汎用性と適用速度です。進化型ヒューリスティック探索プログラム（詳細は後述）に重点を置いた中核的な手法は、多様な数学的構築問題や仮説に迅速に適用可能であり、従来の特注アプローチと比較して、問題固有の専門家による初期の調整が少なくて済む場合が多くあります。深い数学的洞察は当然のことながら問題の定式化と探索空間の定義に役立ちますが、AlphaEvolveは問題ランドスケープ内の微妙な構造を特定することで、効果的な探索パターンと攻撃戦略を自律的に発見する能力をしばしば示します。これにより、多くの異なる問題にまたがる効率的で大規模な探索が可能になります。

これらの発見を可能にした重要な方法論的革新は、AlphaEvolveが構造そのものを直接進化させるのではなく、ヒューリスティックな探索アルゴリズムを進化させる能力にあります。多くの問題、特に数学で一般的な高速な目的関数評価を伴う問題に対して、私たちは反復的な改良戦略を採用しました。AlphaEvolveの各世代は、探索ヒューリスティックを表現するプログラムを進化させるという課題を与えられました。このプログラムには固定された実行時間（例えば1000秒）が与えられ、以前の最良のヒューリスティックによって発見された最良の構成が提示されました。その目的は、この出発点と割り当てられた時間を活用して、さらに優れた構成を見つけることでした。このように、進化プロセスは、既に高品質な解をさらに改善するのに効果的なヒューリスティックを選択します。最終的な構成は、AlphaEvolveによって発見された、異なる特殊なヒューリスティックの連続的な結果であることが多くありました。初期のヒューリスティックは、ランダムまたは単純な初期状態から大きな利益を得ることに長けており、後期のヒューリスティックは、ほぼ最適な構成を微調整することに長けていました。この多段階の適応型探索戦略の自動発見は、手動で再現するのが困難であり、SOTAを超えるために不可欠であることが証明されました。

以下は、AlphaEvolve が新たな結果をもたらしたいくつかの問題についての高レベルの説明です。問題の完全なリストと詳細は付録 B に記載されています。

問題の全リストは付録Bに掲載されており、AlphaEvolveによって発見された新しい構成は付随するGoogle Colabでご覧いただけます。これらの問題と使用された手法に関する詳細な例と詳細は、今後の論文で公開される予定です。これらの発見のほとんどは、外部の数学者であるJavier Gomez Serrano氏とTerence Tao氏から提案された未解決問題に関するもので、両氏はAlphaEvolveへの入力として最適な定式化方法についても助言をいただきました。これは、AlphaEvolveのようなAI駆動型発見エンジンと人間の数学的専門知識との相乗効果を生み出すパートナーシップの可能性を示唆しています。

3.3. Google のコンピューティングエコシステムの最適化

前のセクションで紹介した科学的な応用に加えて、ここでは、AlphaEvolve を使用してミッションクリティカルなインフラストラクチャのパフォーマンスを向上させ、現実世界に影響を与える方法を示します。

3.3.1. データセンターのスケジュールの改善

計算ジョブをマシンのクラスタに効率的にスケジューリングすることは、特に Borg [99] がオーケストレーションした Google のデータセンターの規模では、重要な最適化問題です。このタスクには、ジョブのリソース要件とマシンの容量に基づいて、利用可能なマシンにジョブを割り当てることが含まれます。非効率的な割り当ては、取り残されたリソースにつながる可能性があります。つまり、マシンがある種類のリソース (例: メモリ) を使い果たしたためにジョブを受け付けられなくなったが、他のリソース (例: CPU) はまだ空いているという状況です。スケジューリング効率を改善することで、これらの取り残されたリソースを回復し、同じ量の計算フットプリントでより多くのジョブを完了できるようになります。この回復は、リソース消費を比例的に増加させることなく、増大する計算ニーズに対応するために不可欠です。さらに、この問題は、古典的に難しいビンパッキング問題に加えて、デバッグ可能性やスケールなどの一般的なエンジニアリングの難しさも組み合わされているため、困難です。

図6 | 左：AlphaEvolveによって発見された、Googleのワークロードとキャパシティに合わせて調整されたヒューリスティック関数。右：ヒューリスティックスコアリング関数の視覚化。黄色の領域は高スコア、紫色の領域は低スコアを表します。

我々は、オンラインジョブスケジューリング問題を2変数のベクトルビンパッキング問題として捉えることで、この課題に取り組みます。この文脈において、マシンはCPUとメモリの容量が定義されたビンを表し、受信ジョブは特定のリソース需要を持つアイテムです。ヒューリスティック関数は、保留中のジョブのCPUとメモリの要件、および潜在的なマシンのCPUとメモリの可用性を入力として受け取ります。この関数は、マシンの優先度スコアを出力します。その後、Borgスケジューラは、保留中のジョブを、ヒューリスティック関数によって決定された最高の優先度スコアを持つマシンに割り当てます。このヒューリスティックは、Borgによって各保留中のジョブを実行可能と既に決定されたマシンの順位付けにのみ影響を与えるため、結果として得られるスケジューリング決定は、構成上、事実上正しいものとなります。

AlphaEvolve の初期バージョンは、実稼働環境の既存の機能から進化した、驚くほどシンプルでありながら効果的なヒューリスティック関数（図 6 参照）を発見するために使用されました。Google のデータセンターシミュレーターを使用し、Google の拠点全体のワークロードと容量の履歴スナップショットに基づいて AlphaEvolve にフィードバックを提供します。一般化を確実にするために、最近のワークロードと容量の未公開のテストデータセットで AlphaEvolve のヒューリスティック関数のパフォーマンスを測定します。AlphaEvolve のヒューリスティック関数が実稼働環境のものよりも優れていることを確認したので、AlphaEvolve のヒューリスティック関数を拠点全体に展開しました。Google の拠点全体での展開後の測定により、シミュレーターの結果が確認され、このヒューリスティック関数は、そうでなければ取り残されることになる Google の拠点全体のコンピューティングリソースの平均 0.7% を継続的に回復することが明らかになりました。 AlphaEvolve が深層強化学習アプローチよりも選ばれたのは、そのコードソリューションがパフォーマンスの向上につながるだけでなく、解釈可能性、デバッグ可能性、予測可能性、展開の容易さといった、ミッションクリティカルなシステムに不可欠な品質において明らかな利点も提供するためです。

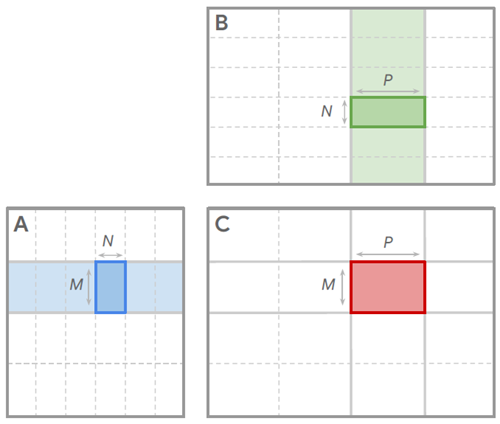
図7 | 行列積 = のタイリングヒューリスティック問題の視覚化。すべての入力形状に対して適切なタイルサイズ ( 、、 ) を自動的に選択するヒューリスティックを作成するのは困難です。これは、行列乗算ユニットの最適な形状とメモリ容量、周囲の演算のメモリ要件、カーネルに組み込まれる追加の演算、低レベルのコンパイラの複雑さなど、さまざまな詳細を知る必要があるためです。

3.3.2. Geminiカーネルエンジニアリングの強化

Gemini のような大規模モデルのトレーニングには、相当量の計算リソースが必要です。Gemini は JAX [9] 上に構築されており、Pallas は JAX の拡張機能で、ハードウェアアクセラレータで最適に実行できるようにカスタマイズされた高度に特殊化されたカスタムプログラム (カーネル) の作成を可能にします。したがって、効率的な Pallas カーネルは Gemini のトレーニングパフォーマンスを最適化するために不可欠です。カーネル最適化の重要な側面は、行列乗算演算のタイリング戦略の調整です (図 7 を参照)。この手法では、大規模な行列乗算計算を小さなサブ問題に分割して、計算とデータ移動のバランスを改善し、全体的な計算を高速化するための鍵となります。従来、カーネルエンジニアは、さまざまな入力形状に対してほぼ最適なタイリング構成を決定するために、検索ベースの自動調整か手動で作成したヒューリスティックのいずれかに依存しています。検索ベースの調整は研究ワークフローを中断するため、入力形状が変わるたびに再調整が必要になります。逆に、効果的なタイリングヒューリスティックを手作業で作成することは、その複雑さゆえにエンジニアリング上の大きなボトルネックとなり、カーネルの機能とハードウェアの複雑な部分の両方を深く理解する必要があります。高性能なヒューリスティックの主な利点は、任意の入力形状に対して高いパフォーマンスを提供できることです。したがって、新興ハードウェア向けの高性能カーネルの設計を迅速化し、モデル開発者による利用を簡素化するために、ヒューリスティック生成プロセスを容易にすることを目指します。

この課題に対処するため、我々は AlphaEvolve を使用して、Gemini のトレーニングに使用される重要な行列乗算カーネルのタイリングヒューリスティックスを最適化します。目的は、カーネルの実際の実行時間を最小限に抑えることです。AlphaEvolve は、候補コードを提案することで、このカーネルのタイリングヒューリスティックスを反復的に探索および改良し、実際の TPU アクセラレータにおけるさまざまな入力形状での実行時間を最小限に抑えることを目指します。AlphaEvolve はカーネルの基礎となる数学的演算を変更するのではなく、タイリング戦略を最適化するため、カーネルの正確性は構築によって維持されます。AlphaEvolve のトレーニングおよび評価データセットを構築するために、カーネルユーザーから現実的なカーネル入力形状を自動的に収集します。これらの入力形状の半分がトレーニングセットを形成し、進化プロセス中に最適化ターゲットを提供します。残りの入力形状は評価セットを形成し、結果として得られるヒューリスティックスの一般的な適用性をテストするために使用されます。

この自動化されたアプローチにより、AlphaEvolve は、既存の専門家が設計したヒューリスティックと比較して、すべてのカーネルで平均 23% のカーネル高速化を実現するヒューリスティックを発見し、それに応じて Gemini の全体的なトレーニング時間を 1% 削減できました。さらに、AlphaEvolve の使用により、カーネルの最適化に要する時間が大幅に短縮され、数か月に及ぶ専用エンジニアリング作業が、わずか数日間の自動化された実験にまで短縮されました。この高速化により、最適化されたカーネルの導入が迅速化され、カーネルエンジニアは専門知識をより戦略的で高レベルの最適化問題に専念できるようになります。さらに、AlphaEvolve は、手動によるチューニングプロセスを自動化し、Gemini カーネルの使用における人間工学的改善への道筋を提供します。AlphaEvolve によって発見されたタイリングヒューリスティックは本番環境に導入され、Gemini のトレーニング効率と Gemini チームの研究およびエンジニアリングの速度を直接的に向上させました。この導入は、Gemini が AlphaEvolve の機能を通じて自身のトレーニングプロセスを最適化するという新しい例でもあります。

3.3.3. ハードウェア回路設計の支援

GoogleのTensor Processing Unit（TPU）などの専用ハードウェアは、現代のAIシステムを大規模に実行するために必要なリソース効率を実現するために不可欠です。しかし、新しいコンピュータチップの設計は複雑で時間のかかるプロセスであり、多くの場合、数年を要します。このプロセスの重要なステップであるレジスタ転送レベル（RTL）の最適化では、電力、性能、面積などの指標を改善するためにハードウェア記述を手作業で書き換える必要があり、高度なスキルを持つエンジニアによる数ヶ月にわたる反復作業が求められます。

本研究では、AlphaEvolveは、行列乗算ユニット内の主要なTPU演算回路について、既に高度に最適化されたVerilog実装を最適化するという課題に取り組みました。最適化の目標は、コンポーネントのコア機能を維持しながら、面積と消費電力の両方を削減することでした。重要な点として、最終提案は、修正された回路が機能的な正当性を維持していることを確認するための堅牢な検証手法に合格する必要がありました。AlphaEvolveは、不要なビットを削除するシンプルなコード書き換えを見つけ出すことができ、この変更はTPU設計者によって正当性が検証されました。この具体的な改善は下流の合成ツールによっても個別に検出されましたが、RTL段階でのAlphaEvolveの貢献は、ソースRTLを改良し、設計フローの早い段階で最適化を提供する能力を実証しています。

次期TPUに統合されるこの改良は、AlphaEvolveを通じてGeminiがTPU演算回路に直接貢献する初の事例であり、将来の貢献への道を開くものです。AlphaEvolveの重要な利点は、ハードウェアエンジニアが使用する標準言語であるVerilogで提案された変更内容を直接伝達できることです。これにより、信頼性が高まり、導入が容易になります。この初期段階の検証は、LLMを活用したコード進化がハードウェア設計を支援し、市場投入までの時間を短縮できるという、革新的なアプローチを実証しています。

3.3.4. コンパイラ生成コードを直接最適化する

トランスフォーマーアーキテクチャ[97]は、LLMからAlphaFold [1]に至るまで、現代のニューラルネットワークの大部分で使用されています。トランスフォーマーの核となる計算はアテンションメカニズム[4]であり、最も一般的にはFlashAttention [21]を使用して実装されています。私たちのスタックでは、FlashAttentionはPallasのアクセラレータカーネルとして実装されており、入力の準備と出力の後処理を行うJAXの高レベルコードでラップされています。機械学習コンパイラ（XLA [74]）は、この実装を一連の中間表現（IR）に変換し、それぞれが特定のハードウェアでの実行のために詳細を追加します。これらの段階で、メモリアクセスオーケストレーションや計算スケジューリングに関する決定を改善することで、特定のハードウェアでの実行時間を大幅に短縮できます。

AlphaEvolveに、FlashAttentionカーネルをカプセル化したXLA生成IR（前処理および後処理コード）を直接最適化するよう依頼しました。GPU上での大規模推論に使用される、非常に影響力のあるトランスフォーマーモデルに対応する構成を最適化し、モジュール全体の実行時間を最小限に抑えることを目標としました。これは特に困難な作業でした。その理由は、(1)IRは開発者が直接編集するのではなくデバッグ用に設計されていること、(2)コンパイラによって生成され、既に高度に最適化されていることです。AlphaEvolveによって提案された各変更は、最適化全体を通して数値的な正確性を保証するために、ランダム化された入力に対する参照（変更されていない）コードと比較されました。最終バージョンのコードは、あらゆる入力に対して正しいことが専門家によって厳密に確認されました。

AlphaEvolveは、IRによって公開された両方の抽象化レベルにおいて、有意義な最適化を提供できました。まず、対象の構成におけるFlashAttentionカーネルは32%高速化されました。次に、AlphaEvolveはカーネル入出力の前処理と後処理の改善を発見し、この部分で15%の高速化を実現しました。これらの結果は、AlphaEvolveがコンパイラ生成コードを最適化する能力を示しており、発見された最適化を特定のユースケース向けに既存のコンパイラに組み込む可能性、あるいは長期的にはAlphaEvolve自体をコンパイラワークフロー自体に組み込む可能性を示唆しています。

4. アブレーション

私たちは、行列乗算を高速化するためのテンソル分解の発見 (セクション 3.1) とキッシング数の下限の計算 (セクション 3.2) という 2 つのタスクのアブレーションを実行し、AlphaEvolve の以下のコンポーネントの有効性を理解することを目指しました。

図8は、包括的なAlphaEvolveアプローチと、上記の様々な代替アプローチの結果を示しています。ご覧のとおり、各コンポーネントが結果の大幅な改善に貢献しています。

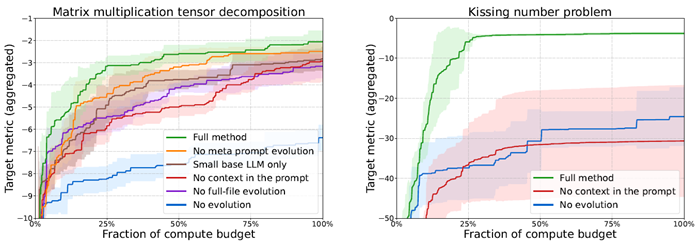
図8 | 左: 行列乗算を高速化するための低ランクテンソル分解を求める問題におけるAlphaEvolveのアブレーション。右: キッシング数を改善するための球面パッキングを求める問題におけるAlphaEvolveのアブレーション。各曲線は、計算予算を増加させた場合の個々の設定のパフォーマンスを、検討対象のすべてのターゲットにおける平均で示しています（ターゲットメトリックの値が高いほど優れています）。陰影は、異なる乱数シードで初期化されたAlphaEvolveの3回の独立した実行における平均のターゲット内標準偏差を示しています。

5. 関連研究

進化的手法　AlphaEvolveは、進化的プログラミング、あるいは遺伝的プログラミング[52]に関する研究の長い伝統を継承する。進化的プログラミングでは、一連の突然変異と交差演算子を繰り返し用いて、プログラムのプールを進化させる[5, 49]。特に、古典的な進化的手法は、記号回帰アプリケーション[64, 84]、自動化された科学的発見[20]またはアルゴリズム的発見[16]、およびスケジューリング[115]の問題において成功を収めてきた。しかし、これらの手法の課題は、手書きの進化演算子を使用することであり、これは設計が難しく、ドメインの重要な特性を捉えられない可能性がある。対照的に、AlphaEvolveはLLMを用いてこれらの演算子の構築を自動化する。つまり、LLMの世界知識を活用して、許可される突然変異演算子のセットを事前に定義することなく、プログラムを突然変異させる。

AlphaEvolveはLLMを用いてこれらの演算子の構築を自動化します。つまり、LLMの世界知識を活用して、許可される突然変異操作のセットを事前に定義することなくプログラムを変化させます。 AlphaEvolveに先立って、LLMと進化を組み合わせた最近の取り組みがいくつかありました。具体的には、Romera-Paredesら[80]が数学的発見へのアプローチとして導入したFunSearchシステムを拡張しています。FunSearchはその後、ベイズ最適化のための獲得関数の学習[2]、認知モデルの発見[13]、グラフ間の距離の計算[100]、組合せ競争プログラミング[98]などの下流タスクで使用されました。AlphaEvolveは、FunSearchとその最近の再実装[23]を3つの重要な点で凌駕しています。まず、FunSearchでは単一のPython関数の進化しか許可されていませんでしたが、AlphaEvolveでは、幅広いプログラミング言語で書かれたコードベース全体の進化を許可しています。第二に、FunSearchは単一の目的関数を最適化していたのに対し、AlphaEvolveは多目的最適化を実行する機能を提供しています。第三に、FunSearchのLLMは比較的小規模で、コードのみで学習されていました。これとは対照的に、AlphaEvolveは最先端のLLMと、豊富な自然言語コンテキストおよびフィードバックを活用しています。本論文で実証したように、これらの拡張により、AlphaEvolveはFunSearchでは対応できなかった重要な難問に取り組むことができます。

このカテゴリーの他の取り組みとしては、シミュレーションされたロボットのセットのためのプログラム的なポリシーを発見するためにLLM誘導進化プロセスを使用するLehmanらによるアプローチ[55]や、コード合成のためのHembergらによるアプローチ[40]がある。同様のアプローチは、記号回帰[34, 86]、組み合わせ最適化のためのヒューリスティックの発見[61, 112, 114]、分子構造の合成[102]など、いくつかの科学的および数学的タスクで使用されている。LLM誘導進化は、LLMプロンプトの強化[26]やニューラルアーキテクチャの探索[14]によってAIシステムを改善するためにも使用されている。AlphaEvolveは、その規模、柔軟性、および幅広いドメインへの一般的な適用性においてこれらのアプローチとは異なる。

近年、LLM誘導進化の基本パラダイムを補完的なアイデアで拡張する研究がいくつか行われています。例えば、Surinaら[93]は強化学習を通してLLMを継続的にfnetuningすることで進化プロセスを補完しています。Grayeliら[34]は、プール内の高性能プログラムを自然言語に要約するLLM誘導概念学習ステップによって進化プロセスを強化しています。AlphaEvolveが動作する規模においてこれらのアイデアの利点を理解するには、さらなる調査が必要です。

進化的手法は、最近のAI Co-Scientist研究 [33] でも活用されています。この研究では、仮説発見、仮説のランク付け、文献レビューといったタスクにそれぞれ異なるエージェントを用いて科学的発見を自動化することを目指しています。AI Co-Scientistが科学的仮説とその評価基準を自然言語で表現するのに対し、AlphaEvolveは進化するコードに焦点を当て、プログラムによる評価関数を用いて進化を指示します。この選択により、LLMの幻覚を大幅に回避することができ、AlphaEvolveは多数のタイムステップにわたって進化プロセスを継続することができます。しかしながら、原理的にはこれら2つのアプローチを組み合わせることが可能であり、自然言語とプログラムによる表現を柔軟に組み合わせる手法が実現可能です。

超最適化とアルゴリズム発見 AlphaEvolveは、実行フィードバックを用いて初期プログラムを反復的に改善するという点で、コードの超最適化の手法と見なすことができます。コードの超最適化のアイデアは1980年代に遡ります[67]。LLM以前のこの問題へのアプローチには、体系的列挙[67]、遺伝的探索[19]、モンテカルロサンプリング[83]、深層強化学習[66]などがありました。さらに、行列乗算などの単一の問題に焦点を当てた限定的な設定では、AlphaTensorなどのシステムが証明可能に正しいアルゴリズムを発見することもできました[25]。

最近では、LLMをベースにした超最適化とアルゴリズム発見へのアプローチが数多く登場しています。これらの研究は、コーディングタスクにおけるLLMの成功に基づいており、AlphaCode [58]のような（シミュレーションによる）プログラミング競技での成功がその好例でしょう。例えば、LLMエージェントは、アテンション演算 [15] や、より一般的なユーザー指定演算 [54] など、GPUカーネルの特定の演算を最適化するために使用されています。また、LLMを用いて新しい進化アルゴリズムを発見する研究 [53]、言語モデルの訓練 [56]、ウェアハウス規模のコンピュータを最適化する研究 [59] もあります。その他の最近の研究 [105] では、数学的タスクとコーディングタスクを実行するために、複数のLLMエージェントが互いに対話する手法も提案されています。

LLM をアルゴリズム発見に使用するこれまでの研究では有望な結果が得られていますが、進化アルゴリズムに LLM を活用する AlphaEvolve のアプローチにより、第 3 章で示すように、はるかに困難な問題に取り組むことができます。

科学的および数学的発見のためのAI　過去10年間で、AIシステムはタンパク質構造予測[45]から量子物理学[6、81]、気候科学[51]まで、幅広い科学分野とタスクに適用されてきました。特に、材料科学[44、69、91、116]、化学[12、62]、バイオインフォマティクス[65、82]、地球科学[76]、量子物理学[29、75]など、複数の分野の科学的問題を対象としたLLMベースの最近の方法が数多くあります（このトピックに関する調査については、[35、63、78]を参照）。

これらの手法の多くは、科学的発見プロセスのいくつかの異なる段階を自動化するために LLM を使用しています [36, 57, 103, 106, 109]。たとえば、仮説やアイデアの生成とランク付けなどです [37, 87]。これらの方法のうち、特に AlphaEvolve に関連するのは、LLM 誘導ツリー検索ベースアルゴリズム [11] や LLM 誘導進化アルゴリズム [33, 110, 117] を使用する方法です。他の研究では、LLM を使用して実験の計画と設計 [7, 10, 42, 72] や実験の実行とワークフロー [27, 60, 79, 102, 113] を最適化しています。最後に、データ分析段階に焦点を当てた研究もあります [77]。AlphaEvolve は、プログラム的な仮説表現と評価指標を使用する点で、これらの方法のほとんどと異なります。

AIシステムは純粋数学の進歩にも貢献してきました[22]。この文脈において、FunSearchアプローチ[23, 80]は、数学的命題の証拠と反例を発見するための強力なツールとしてLLM誘導進化を確立しました。これは、数学的命題の形式的および非形式的証明を見つける問題と相補的な問題です[3, 18, 95, 96, 107, 108]。

6. 考察

AlphaEvolve は、最先端の LLM と進化的フレームワーク内の自動評価メトリックを組み合わせることで得られる驚くべきパワーを実証しており、数十年前の数学的問題に関する新たな発見や、高度に最適化されたコンピューティングスタックの実用的な改善につながる可能性があります。

興味深いことに、AlphaEvolveは、同じ問題に異なる方法でアプローチすることを可能にします。例えば、解を直接探索する、解をゼロから構築する関数を見つける、あるいは解を見つけるための探索アルゴリズムを進化させるなどです。AlphaEvolveを異なる方法で適用すると、それぞれ異なるバイアスが生じます（例えば、構成関数を見つけると、対称性の高いオブジェクトを発見しやすくなる可能性があります[80]）。そのため、AlphaEvolveは異なる問題に適用できます。

AlphaEvolveは、進化的プロセスを通じてベースLLMの能力を大幅に向上させるテスト時計算エージェントとも捉えることができます（例えば、繰り返しサンプリングと比較して）。これは、機械フィードバックがテスト時計算を、新たな科学的発見や非常に価値の高い実用的な最適化が行われる領域までスケールアップし続けることをいかにして維持できるかを示す、説得力のあるデモンストレーションと言えるでしょう。一方で、自然な次のステップとして、AlphaEvolveによって強化されたベースLLMの性能を次世代のベースモデルに取り込むことを検討することが挙げられます。これは本質的な価値を持つ可能性があり、AlphaEvolveの次期バージョンの向上にも繋がる可能性も高いでしょう。

蒸留の他にも、AlphaEvolveが独自のインフラストラクチャと（将来のバージョンの）ベースLLMの効率性を向上させる実用的な発見を行えるという点も興味深い点です。現時点では、その効果は中程度で、次期バージョンのAlphaEvolveを改善するためのフィードバックループには数ヶ月かかります。しかし、これらの改善により、堅牢な評価関数を備えた環境（問題）を複数設定することの価値がより広く認識され、ひいては今後、より価値の高い実用的な発見につながると期待しています。

AlphaEvolveの主な限界は、自動評価器を設計できる問題しか扱えないことです。これは数学および計算科学の多くの問題に当てはまりますが、自然科学など、一部の実験しかシミュレーションや自動化ができない分野もあります。AlphaEvolveはLLMによるアイデアの評価を可能にしますが、これは私たちが最適化した設定ではありません。しかし、同時並行研究によりこれが可能であることが示されており[33]、2つの設定を連携させ、LLMが高レベルのアイデアに関するフィードバックを提供し、その後実装段階に移行し、コード実行を通じて機械からのフィードバックを得るという自然な流れになるでしょう。

謝辞

このホワイトペーパーをレビューしていただいたMichael Figurnov氏、初期の調査と洞察に満ちた議論をしてくださったAlhussein Fawzi氏、Bernardino Romera-Paredes氏、Ankit Anand氏、サポートとアドバイスをしてくださったStig Petersen氏とDemis Hassabis氏、実用的なアプリケーションの管理に関する有益なアドバイスをしてくださったJD Velasquez氏、そしてAlphaEvolveの初期ユーザーと協力者の皆様には、多様なユースケースと洞察に満ちたフィードバックを提供してくださったことに感謝いたします。これらの方々のおかげで、AlphaEvolveは幅広いアプリケーションに対応する、より堅牢で汎用性の高いツールへと進化しました。このホワイトペーパーで取り上げたアプリケーションへの、これらの方々の貴重な貢献に深く感謝いたします。

具体的な未解決の数学問題を提案し、AlphaEvolve に最適な定式化方法をアドバイスしてくれた Terence Tao、Javier Gomez Serrano、Jordan Ellenberg に感謝します。また、そのような問題に AlphaEvolve を適用する貢献をした Bogdan Georgiev と Johannes Bausch にも感謝します。

データセンターのスケジューリングへの応用を共同で主導してくれた Mohammadamin Barekatain、Patrick Heisel、Chase Hensel、Robert O’Callahan、Pengming Wang に感謝します。多大な貢献をしてくれた Federico Piccinini、Sultan Kenjeyev、Andrea Michi に感謝します。有益なアドバイスを提供してくれた Kieran Milan、Daniel Mankowitz、Cosmin Paduraru、Calin Cascaval、Tammo Spalink、Natasha Antropova に感謝します。この研究をレビューしてくれた Aaron Gentleman、Gaurav Dhiman、Parthasarathy Ranganatha、Amin Vahdat に感謝します。

Gemini カーネルエンジニアリングへのアプリケーションをリードした Yanislav Donchev 氏、多大な貢献をした Richard Tan-burn 氏、役立つアドバイスを提供してくれた Justin Chiu 氏と Julian Walker 氏、この作業をレビューした Jean-Baptiste Alayrac 氏、Dmitry Lepikhin 氏、Sebastian Borgeaud 氏、Koray Kavukcuoglu 氏、Jef Dean 氏に感謝します。

TPU 回路設計への応用を主導した Timur Sitdikov 氏、回路評価インフラストラクチャを提供した Georges Rotival 氏、TPU 設計の結果の検証と妥当性確認を行った Kirk Sanders 氏、Srikanth Dwarakanath 氏、Indranil Chakraborty 氏、Christopher Clark 氏、有益なアドバイスをくれた Vinod Nair 氏、Sergio Guadarrama 氏、Dimitrios Vytiniotis 氏、Daniel Belov 氏、本研究をレビューした Kerry Takenaka 氏、Jef Dean 氏、Sridhar Lakshmanamurthy 氏、Parthasarathy Ranganathan 氏、Amin Vahdat 氏に感謝します。

XLA の変更に協力し、有益なアドバイスをくれた Benjamin Chetioui、Sergei Lebedev、Alexander Belyaev、Henning Becker、Oleg Shyshkov、Aliia Khasanova、本研究をレビューしてくれた Giorgio Arena、Marco Cornero、Sebastian Bodenstein に感謝します。

著者情報

以下の著者が同等の貢献をしました：Alexander Novikov、Ngân Vu、Marvin Eisenberger、Emilien˜ Dupont、Po-Sen Huang、Adam Zsolt Wagner、Sergey Shirabokov、Borislav Kozlovskii、およびMatej Balog。

貢献：A.N. と M.B. は、AlphaEvolve の初期バージョンを設計および実装しました。M.B.、A.N.、N.V.、および P.K. は、プロジェクトのビジョンを策定し、問題をスコープ設定しました。N.V. と P.- S.H. は、実際のアプリケーションを監督しました。E.D. と M.E. は、F.J.R.R. と M.B. からの入力に基づいて、AlphaEvolve の反復処理に使用される最初のベンチマーク問題を実装しました。A.N. と M.E. は、S.S.、P.-S.H. の貢献と、M.B.、E.D.、A.Z.W.、および N.V. からの入力に基づいて、AlphaEvolve の最終バージョンを開発しました。A.N.、S.S.、P.-S.H.、および M.E. は、AlphaEvolve の基盤となるインフラストラクチャを保守しました。M.E. と E.D. F.J.R.R. からの情報提供を受け、AlphaEvolve を使用して行列乗算の新しいアルゴリズムを発見しました。A.Z.W. は、A.M.、M.E.、A.N. の協力を得て、未解決の数学問題への応用に取り組みました。A.N. は、Borg スケジューリングアプリケーションに貢献しました。P.-S.H. と N.V. は、Gemini カーネルエンジニアリングへの応用に取り組みました。P.-S.H. と A.N. は、TPU 回路設計アプリケーションに貢献しました。B.K. と S.S. は、AlphaEvolve を適用してコンパイラ生成コードを直接最適化する作業に取り組みました。M.E. はアブレーション実験を実施しました。M.B.、A.N.、M.E.、S.S.、および P.-S. H. は、コードレビューの大部分を実施しました。 M.B.、E.D.、S.C.、N.V.、A.Z.W.、F.J.R.R.、M.E.、A.N.、B.K.、S.S.、A.M.、M.P.K.がA.S.、P.-S.H、P.K.の協力を得て論文を執筆しました。N.V.、E.D.、M.E.、S.C.、A.N.、A.Z.W.は図を作成しました。F.J.R.R.、A.M.、A.Z.W.は付随するGoogle Colabを組み立てました。S.N.、A.D.、P.K.は本研究の複数の分野に助言と支援を提供しました。M.B.、A.N.、N.V.、G.H.はチームの調整役を務めました。P.K.は研究プログラムの監督と調整役を務めました。

参考文献

[1] J. Abramson, J. Adler, J. Dunger, R. Evans, T. Green, A. Pritzel, O. Ronneberger, L. Will- more, A. J. Ballard, J. Bambrick, et al. Accurate structure prediction of biomolecular interactions with alphafold 3. Nature, 630(8016):493–500, 2024.

[2] V. Aglietti, I. Ktena, J. Schrouf, E. Sgouritsa, F. J. R. Ruiz, A. Malek, A. Bellot, and S. Chiappa. FunBO: Discovering acquisition functions for Bayesian optimization with FunSearch. In International Conference on Machine Learning, 2025.

[3] AlphaProof and AlphaGeometry teams. AI achieves silver-medal standard solving International Mathematical Olympiad problems, 2024. URL https://deepmind.g oogle/discover/blog/ai-solves-imo-problems-at-silver-medal-lev el.

[4] D. Bahdanau, K. Cho, and Y. Bengio. Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473, 2014.

[5] W. Banzhaf, P. Nordin, R. E. Keller, and F. D. Francone. Genetic Programming: An Introduction on the Automatic Evolution of computer programs and its Applications. The Morgan Kaufmann Series in Artifcial Intelligence, 1998.

[6] J. Bausch, A. W. Senior, F. J. H. Heras, T. Edlich, A. Davies, M. Newman, C. Jones, K. Satzinger, M. Y. Niu, S. Blackwell, G. Holland, D. Kafri, J. Atalaya, C. Gidney, D. Hassabis, S. Boixo, H. Neven, and P. Kohli. Learning high-accuracy error decoding for quantum processors. Nature, 635(8040):834–840, 2024. doi: 10.1038/s41586-0 24-08148-8.

[7] D. A. Boiko, R. MacKnight, B. Kline, and G. Gomes. Autonomous chemical research with large language models. Nature, 624(7992):570–578, 2023. doi: 10.1038/s415 86-023-06792-0.

[8] P. Boyvalenkov, S. Dodunekov, and O. Musin. A survey on the kissing numbers. Serdica Math. J., 38(4):507–522, 2012. ISSN 1310-6600.

[9] J. Bradbury, R. Frostig, P. Hawkins, M. J. Johnson, C. Leary, D. Maclaurin, G. Necula, A. Paszke, J. VanderPlas, S. Wanderman-Milne, and Q. Zhang. JAX: composable transformations of Python+NumPy programs, 2018. URL http://github.com/j ax-ml/jax.

[10] A. M. Bran, S. Cox, O. Schilter, C. Baldassari, A. D. White, and P. Schwaller. Augmenting large language models with chemistry tools. Nature Machine Intelligence, 6(5):525– 535, 2024. doi: 10.1038/s42256-024-00832-8.

[11] A. M. Bran, T. A. Neukomm, D. P. Armstrong, Z. Jončev, and P. Schwaller. Chemical reasoning in LLMs unlocks steerable synthesis planning and reaction mechanism elucidation. In arXiv preprint arXiv:2503.08537, 2025.

[12] M. Caldas Ramos, C. J. Collison, and A. D. White. A review of large language models and autonomous agents in chemistry. Chemical Science, 16:2514–2572, 2025. doi: 10.1039/D4SC03921A.

[13] P. S. Castro, N. Tomasev, A. Anand, N. Sharma, R. Mohanta, A. Dev, K. Perlin, S. Jain, K. Levin, N. Éltető, W. Dabney, A. Novikov, G. C. Turner, M. K. Eckstein, N. D. Daw, K. J. Miller, and K. L. Stachenfeld. Discovering symbolic cognitive models from human and animal behavior. In International Conference on Machine Learning, 2025.

[14] A. Chen, D. M. Dohan, and D. R. So. EvoPrompting: Language models for code-level neural architecture search. In Advances in Neural Information Processing Systems, 2023.

[15] T. Chen, B. Xu, and K. Devleker. Automating GPU kernel generation with DeepSeek-R1 and inference time scaling, 2025. URL https://developer.nvidia.com/blog/ automating-gpu-kernel-generation-with-deepseek-r1-and-inference- time-scaling.

[16] X. Chen, C. Liang, D. Huang, E. Real, K. Wang, H. Pham, X. Dong, T. Luong, C.-J. Hsieh, Y. Lu, and Q. V. Le. Symbolic discovery of optimization algorithms. Advances in Neural Information Processing Systems, 2023.

[17] A. Cloninger and S. Steinerberger. On suprema of autoconvolutions with an application to Sidon sets. Proceedings of the American Mathematical Society, 145(8):3191–3200, 2017.

[18] K. M. Collins, A. Q. Jiang, S. Frieder, L. Wong, M. Zilka, U. Bhatt, T. Lukasiewicz, Y. Wu, J. B. Tenenbaum, W. Hart, et al. Evaluating language models for mathematics through interactions. Proceedings of the National Academy of Sciences, 121(24):e2318124121, 2024.

[19] K. D. Cooper, D. Subramanian, and L. Torczon. Adaptive optimizing compilers for the 21st century. The Journal of Supercomputing, 23:7–22, 2002.

[20] M. Cranmer. Interpretable machine learning for science with pysr and symbolicre- gression. jl. arXiv preprint arXiv:2305.01582, 2023.

[21] T. Dao, D. Fu, S. Ermon, A. Rudra, and C. Ré. Flashattention: Fast and memory- efcient exact attention with io-awareness. Advances in neural information processing systems, 35:16344–16359, 2022.

[22] A. Davies, P. Veličković, L. Buesing, S. Blackwell, D. Zheng, N. Tomašev, R. Tanburn, P. Battaglia, C. Blundell, A. Juhász, M. Lackenby, G. Williamson, D. Hassabis, and P. Kohli. Advancing mathematics by guiding human intuition with AI. Nature, 600 (7887):70–74, 2021. doi: 10.1038/s41586-021-04086-x.

[23] J. S. Ellenberg, C. S. Fraser-Taliente, T. R. Harvey, K. Srivastava, and A. V. Sutherland. Generative modelling for mathematical discovery. arXiv preprint arXiv:2503.11061, 2025.

[24] P. Erdős. Some remarks on number theory. Riveon Lematematika, 9:45–48, 1955.

[25] A. Fawzi, M. Balog, A. Huang, T. Hubert, B. Romera-Paredes, M. Barekatain, A. Novikov, F. J. R. Ruiz, J. Schrittwieser, G. Swirszcz, D. Silver, D. Hassabis, and P. Kohli. Discov- ering faster matrix multiplication algorithms with reinforcement learning. Nature, 610(7930):47–53, 2022. doi: 10.1038/s41586-022-05172-4.

[26] C. Fernando, D. Banarse, H. Michalewski, S. Osindero, and T. Rocktäschel. Prompt- breeder: Self-referential self-improvement via prompt evolution. arXiv preprint arXiv:2309.16797, 2023.

[27] N. Ferruz and B. Höcker. Controllable protein design with language models. Nature Machine Intelligence, 4(6):521–532, 2022.

[28] E. Friedman. Erich’s Packing Center. https://erich-friedman.github.io/pac king/, 2025. Accessed: 2025-04-22.

[29] F. Frohnert, X. Gu, M. Krenn, and E. van Nieuwenburg. Discovering emergent connec- tions in quantum physics research via dynamic word embeddings. Machine Learning: Science and Technology, 6(1):015029, 2025. doi: 10.1088/2632-2153/adb00a.

[30] M. Ganzhinov. Highly symmetric lines. In arXiv preprint arXiv:2207.08266v1, 2022.

[31] Gemini team. Gemini 2.5: Our most intelligent AI model, 2025. URL https: //blog.google/technology/google-deepmind/gemini-model-thinking-u pdates-march-2025.

[32] F. Gonçalves, D. O. e Silva, and S. Steinerberger. Hermite polynomials, linear fows on the torus, and an uncertainty principle for roots. Journal of Mathematical Analysis and Applications, 451(2):678–711, 2017.

[33] J. Gottweis, W.-H. Weng, A. Daryin, T. Tu, A. Palepu, P. Sirkovic, A. Myaskovsky, F. Weissenberger, K. Rong, R. Tanno, K. Saab, D. Popovici, J. Blum, F. Zhang, K. Chou, A. Hassidim, B. Gokturk, A. Vahdat, P. Kohli, Y. Matias, A. Carroll, K. Kulkarni, N. Tomasev, Y. Guan, V. Dhillon, E. D. Vaishnav, B. Lee, T. R. D. Costa, J. R. Penadés, G. Peltz, Y. Xu, A. Pawlosky, A. Karthikesalingam, and V. Natarajan. Towards an AI co-scientist. arXiv preprint arXiv:2502.18864, 2025.

[34] A. Grayeli, A. Sehgal, O. Costilla Reyes, M. Cranmer, and S. Chaudhuri. Symbolic regression with a learned concept library. Advances in Neural Information Processing Systems, 37:44678–44709, 2024.

[35] M. Gridach, J. Nanavati, C. Mack, K. Z. E. Abidine, and L. Mendes. Agentic AI for scientifc discovery: A survey of progress, challenges, and future directions. In ICLR Workshop: Towards Agentic AI for Science: Hypothesis Generation, Comprehension, Quantifcation, and Validation, 2025.

[36] X. Gu and M. Krenn. Interesting scientifc idea generation using knowledge graphs and LLMs: Evaluations with 100 research group leaders. In arXiv preprint arXiv:2405.17044, 2024.

[37] S. Guo, A. H. Shariatmadari, G. Xiong, and A. Zhang. Embracing foundation models for advancing scientifc discovery. In Proceedings of the IEEE International Conference on Big Data, pages 1746–1755, 2024. doi: 10.1109/bigdata62323.2024.10825618.

[38] K. Gyarmati, F. Hennecart, and I. Z. Ruzsa. Sums and diferences of fnite sets. Functiones et Approximatio Commentarii Mathematici, 37(1):175–186, 2007.

[39] J. K. Haugland. The minimum overlap problem revisited. arXiv:1609.08000, 2016. arXiv preprint

[40] E. Hemberg, S. Moskal, and U.-M. O’Reilly. Evolving code with a large language model. Genetic Programming and Evolvable Machines, 25(2):21, 2024. doi: 10.1007/ s10710-024-09494-2.

[41] J. E. Hopcroft and L. R. Kerr. On minimizing the number of multiplications necessary for matrix multiplication. SIAM J. Appl. Math., 20(1):30–36, Jan. 1971. ISSN 0036- 1399. doi: 10.1137/0120004.

[42] K. Huang, Y. Qu, H. Cousins, W. A. Johnson, D. Yin, M. Shah, D. Zhou, R. Altman, M. Wang, and L. Cong. CRISPR-GPT: An LLM agent for automated design of gene- editing experiments. In arXiv preprint arXiv:2404.18021, 2024.

[43] L. Huang, W. Yu, W. Ma, W. Zhong, Z. Feng, H. Wang, Q. Chen, W. Peng, X. Feng, B. Qin, et al. A survey on hallucination in large language models: Principles, taxonomy, challenges, and open questions. ACM Transactions on Information Systems, 43(2): 1–55, 2025.

[44] S. Jia, C. Zhang, and V. Fung. LLMatDesign: Autonomous materials discovery with large language models. In arXiv preprint arXiv:2406.13163, 2024.

[45] J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvu- nakool, R. Bates, A. Žídek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bo- denstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli, and D. Hassabis. Highly accurate protein structure prediction with AlphaFold. Nature, 596(7873): 583–589, 2021. doi: 10.1038/s41586-021-03819-2.

[46] M. Kauers and J. Moosbauer. Flip graphs for matrix multiplication. In Proceedings of the 2023 International Symposium on Symbolic and Algebraic Computation, pages 381–388, 2023.

[47] M. Kauers and J. Moosbauer. Some new non-commutative matrix multiplication algorithms of size ( , ,6). ACM Commun. Comput. Algebra, 58(1):1–11, Jan. 2025. ISSN 1932-2232. doi: 10.1145/3712020.3712021.

[48] D. P. Kingma and J. Ba. Adam: A method for stochastic optimization. In International Conference on Learning Representations (ICLR), 2015.

[49] J. R. Koza. Genetic programming as a means for programming computers by natural selection. Statistics and Computing, 4(2):87–112, 1994. doi: 10.1007/BF00175355.

[50] J. D. Laderman. A noncommutative algorithm for multiplying 3 × 3 matrices using 23 multiplications. Bulletin of the American Mathematical Society, 82(1):126 – 128, 1976.

[51] R. Lam, A. Sanchez-Gonzalez, M. Willson, P. Wirnsberger, M. Fortunato, F. Alet, S. Ravuri, T. Ewalds, Z. Eaton-Rosen, W. Hu, A. Merose, S. Hoyer, G. Holland, O. Vinyals, J. Stott, A. Pritzel, S. Mohamed, and P. Battaglia. Learning skillful medium-range global weather forecasting. Science, 382(6677):1416–1421, 2023. doi: 10.1126/science.adi2336.

[52] W. B. Langdon and R. Poli. Foundations of genetic programming. Springer Science & Business Media, 2013.

[53] R. Lange, Y. Tian, and Y. Tang. Large language models as evolution strategies. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, GECCO ’24 Companion, pages 579–582. Association for Computing Machinery, 2024. doi: 10.1145/3638530.3654238.

[54] R. T. Lange, A. Prasad, Q. Sun, M. Faldor, Y. Tang, and D. Ha. The AI CUDA engineer: Agentic CUDA kernel discovery, optimization and composition. Technical report, Sakana AI, 02 2025.

[55] J. Lehman, J. Gordon, S. Jain, K. Ndousse, C. Yeh, and K. O. Stanley. Evolution through large models. In Handbook of evolutionary machine learning, pages 331–366. Springer, 2023.

[56] J. Lehman, J. Gordon, S. Jain, K. Ndousse, C. Yeh, and K. O. Stanley. Evolution Through Large Models, pages 331–366. Springer Nature Singapore, 2024. doi: 10.1007/978-981-99-3814-8\_11.

[57] P.-H. Li, Y.-Y. Sun, H.-F. Juan, C.-Y. Chen, H.-K. Tsai, and J.-H. Huang. A large language model framework for literature-based disease–gene association prediction. Briefngs in Bioinformatics, 26(1):bbaf070, 02 2025. ISSN 1477-4054. doi: 10.1093/bib/bbaf070.

[58] Y. Li, D. Choi, J. Chung, N. Kushman, J. Schrittwieser, R. Leblond, T. Eccles, J. Keeling, F. Gimeno, A. D. Lago, T. Hubert, P. Choy, C. de Masson d’Autume, I. Babuschkin, X. Chen, P.-S. Huang, J. Welbl, S. Gowal, A. Cherepanov, J. Molloy, D. J. Mankowitz, E. S. Robson, P. Kohli, N. de Freitas, K. Kavukcuoglu, and O. Vinyals. Competition- level code generation with AlphaCode. Science, 378(6624):1092–1097, 2022. doi: 10.1126/science.abq1158.

[59] H. Lin, M. Maas, M. Roquemore, A. Hasanzadeh, F. Lewis, Y. Simonson, T.-W. Yang, A. Yazdanbakhsh, D. Altinbüken, F. Papa, et al. ECO: An LLM-driven efcient code optimizer for warehouse scale computers. arXiv preprint arXiv:2503.15669, 2025.

[60] Z. Lin, H. Akin, R. Rao, B. Hie, Z. Zhu, W. Lu, N. Smetanin, R. Verkuil, O. Kabeli, Y. Shmueli, A. dos Santos Costa, M. Fazel-Zarandi, T. Sercu, S. Candido, and A. Rives. Evolutionary-scale prediction of atomic-level protein structure with a language model. Science, 379(6637):1123–1130, 2023. doi: 10.1126/science.ade2574.

[61] F. Liu, X. Tong, M. Yuan, X. Lin, F. Luo, Z. Wang, Z. Lu, and Q. Zhang. Evolution of heuristics: Towards efcient automatic algorithm design using large language model. arXiv preprint arXiv:2401.02051, 2024.

[62] F. Luo, J. Zhang, Q. Wang, and C. Yang. Leveraging prompt engineering in large language models for accelerating chemical research. ACS Central Science, 2025. doi: 10.1021/acscentsci.4c01935.

[63] Z. Luo, Z. Yang, Z. Xu, W. Yang, and X. Du. LLM4SR: A survey on large language models for scientifc research. In arXiv preprint arXiv:2501.04306, 2025.

[64] H. Ma, A. Narayanaswamy, P. Riley, and L. Li. Evolving symbolic density functionals. Science Advances, 8(36):eabq0279, 2022. doi: 10.1126/sciadv.abq0279.

[65] A. Madani, B. Krause, E. R. Greene, S. Subramanian, B. P. Mohr, J. M. Holton, J. L. Olmos, C. Xiong, Z. Z. Sun, R. Socher, J. S. Fraser, and N. Naik. Large language models generate functional protein sequences across diverse families. Nature Biotechnology, 41 (8):1099–1106, August 2023. ISSN 1087-0156. doi: 10.1038/s41587-022-01618-2.

[66] D. J. Mankowitz, A. Michi, A. Zhernov, M. Gelmi, M. Selvi, C. Paduraru, E. Leurent, S. Iqbal, J.-B. Lespiau, A. Ahern, T. Köppe, K. Millikin, S. Gafney, S. Elster, J. Broshear, C. Gamble, K. Milan, R. Tung, M. Hwang, T. Cemgil, M. Barekatain, Y. Li, A. Mandhane, T. Hubert, J. Schrittwieser, D. Hassabis, P. Kohli, M. Riedmiller, O. Vinyals, and D. Silver. Faster sorting algorithms discovered using deep reinforcement learning. Nature, 618 (7964):257–263, 2023. doi: 10.1038/s41586-023-06004-9.

[67] H. Massalin. Superoptimizer - A look at the smallest program. In R. H. Katz and M. Freeman, editors, Proceedings of the Second International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS II), Palo Alto, California, USA, October 5-8, 1987, pages 122–126. ACM Press, 1987. doi: 10.1145/ 36206.36194.

[68] M. Matolcsi and C. Vinuesa. Improved bounds on the supremum of autoconvolutions. Journal of mathematical analysis and applications, 372(2):439–447, 2010.

[69] S. Miret and N. M. A. Krishnan. Are LLMs ready for real-world materials discovery? In arXiv preprint arXiv:2402.05200, 2024.

[70] J. Moosbauer and M. Poole. Flip graphs with symmetry and new matrix multiplication schemes. arXiv preprint arXiv:2502.04514, 2025.

[71] J.-B. Mouret and J. Clune. Illuminating search spaces by mapping elites. arXiv preprint arXiv:1504.04909, 2015.

[72] V. Naumov, D. Zagirova, S. Lin, Y. Xie, W. Gou, A. Urban, N. Tikhonova, K. Alawi, M. Durymanov, F. Galkin, S. Chen, D. Sidorenko, M. Korzinkin, M. Scheibye-Knudsen, A. Aspuru-Guzik, E. Izumchenko, D. Gennert, F. W. Pun, M. Zhang, P. Kamya, A. Aliper, F. Ren, and A. Zhavoronkov. DORA AI scientist: Multi-agent virtual research team for scientifc exploration discovery and automated report generation. In bioRxiv preprint:10.1101/2025.03.06.641840. Cold Spring Harbor Laboratory, 2025. doi: 10.1101/2025.03.06.641840.

[73] OpenAI. Introducing OpenAI o3 and o4-mini, 2025. URL https://openai.com/i ndex/introducing-o3-and-o4-mini/.

[74] OpenXLA. XLA: composable transformations of Python+NumPy programs. URL https://github.com/openxla/xla.

[75] H. Pan, N. Mudur, W. Taranto, M. Tikhanovskaya, S. Venugopalan, Y. Bahri, M. P. Brenner, and E.-A. Kim. Quantum many-body physics calculations with large language models. Communications Physics, 8(1):49, 2025. doi: 10.1038/s42005-025-01956-y.

[76] D. Pantiukhin, B. Shapkin, I. Kuznetsov, A. A. Jost, and N. Koldunov. Accelerating Earth science discovery via multi-agent LLM systems. In arXiv preprint arXiv:2503.05854, 2025.

[77] Z. Rasheed, M. Waseem, A. Ahmad, K.-K. Kemell, W. Xiaofeng, A. N. Duc, and P. Abra- hamsson. Can large language models serve as data analysts? a multi-agent assisted approach for qualitative data analysis. arXiv preprint arXiv:2402.01386, 2024.

[78] S. Ren, P. Jian, Z. Ren, C. Leng, C. Xie, and J. Zhang. Towards scientifc intelligence: A survey of LLM-based scientifc agents. In arXiv preprint arXiv:2503.24047, 2025.

[79] A. Rives, J. Meier, T. Sercu, S. Goyal, Z. Lin, J. Liu, D. Guo, M. Ott, C. L. Zitnick, J. Ma, and R. Fergus. Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences. Proceedings of the National Academy of Sciences, 118(15):e2016239118, 2021. doi: 10.1073/pnas.2016239118.

[80] B. Romera-Paredes, M. Barekatain, A. Novikov, M. Balog, M. P. Kumar, E. Dupont, F. J. R. Ruiz, J. Ellenberg, P. Wang, O. Fawzi, P. Kohli, and A. Fawzi. Mathematical discoveries from program search with large language models. Nature, 625(7995): 468–475, 2023. doi: 10.1038/s41586-023-06924-6.

[81] F. J. R. Ruiz, T. Laakkonen, J. Bausch, M. Balog, M. Barekatain, F. J. H. Heras, A. Novikov, N. Fitzpatrick, B. Romera-Paredes, J. van de Wetering, A. Fawzi, K. Me- ichanetzidis, and P. Kohli. Quantum circuit optimization with AlphaTensor. Nature Machine Intelligence, 7(3):374–385, 2025. doi: 10.1038/s42256-025-01001-1.

[82] O. A. Sarumi and D. Heider. Large language models and their applications in bioinfor- matics. Computational and Structural Biotechnology Journal, 23:3498–3505, 2024. ISSN 2001-0370. doi: https://doi.org/10.1016/j.csbj.2024.09.031.

[83] E. Schkufza, R. Sharma, and A. Aiken. Stochastic superoptimization. In V. Sarkar and R. Bodík, editors, Architectural Support for Programming Languages and Operating Systems, ASPLOS 2013, Houston, TX, USA, March 16-20, 2013, pages 305–316. ACM, 2013. doi: 10.1145/2451116.2451150.

[84] M. Schmidt and H. Lipson. Distilling free-form natural laws from experimental data. Science, 324(5923):81–85, 2009. doi: 10.1126/science.1165893.

[85] N. Shinn, F. Cassano, A. Gopinath, K. Narasimhan, and S. Yao. Refexion: Language agents with verbal reinforcement learning. Advances in Neural Information Processing Systems, 36:8634–8652, 2023.

[86] P. Shojaee, K. Meidani, S. Gupta, A. B. Farimani, and C. K. Reddy. LLM-SR: Scientifc equation discovery via programming with large language models. In International Conference on Learning Representations, 2025.

[87] C. Si, D. Yang, and T. Hashimoto. Can LLMs generate novel research ideas? a large- scale human study with 100+ NLP researchers. In International Conference on Learning Representations, 2025.

[88] A. Smirnov. Several bilinear algorithms for matrix multiplication problems ⟨3, , ⟩. https://www.researchgate.net/publication/350897049_Several_Bilin ear_Algorithms_for_Matrix_Multiplication_Problems_3_P_Q, 04 2021.

[89] A. Smirnov. Bilinear algorithm for matrix multiplication ⟨4×4×9; 104⟩. an irreducibly irrational solution of the brent system? https://www.researchgate.net/publi cation/364167198_Bilinear_Algorithm_for_Matrix_Multiplication_4 x4x9_104_An_irreducibly_irrational_solution_of_the_Brent_system, 10 2022.

[90] A. V. Smirnov. The bilinear complexity and practical algorithms for matrix multipli- cation. Computational Mathematics and Mathematical Physics, 53(12):1781–1795, 2013.

[91] Z. Song, M. Ju, C. Ren, Q. Li, C. Li, Q. Zhou, and J. Wang. LLM-Feynman: Leveraging large language models for universal scientifc formula and theory discovery. In arXiv preprint arXiv:2503.06512, 2025.

[92] V. Strassen. Gaussian elimination is not optimal. Numerische mathematik, 13(4): 354–356, 1969.

[93] A. Surina, A. Mansouri, L. Quaedvlieg, A. Seddas, M. Viazovska, E. Abbe, and C. Gul- cehre. Algorithm discovery with LLMs: Evolutionary search meets reinforcement learning. In arXiv preprint arXiv:2504.05108, 2025.

[94] R. Tanese. Distributed genetic algorithms for function optimization. University of Michigan, 1989.

[95] A. Thakur, G. Tsoukalas, Y. Wen, J. Xin, and S. Chaudhuri. An in-context learning agent for formal theorem-proving. In Conference on Language Models, 2024.

[96] T. H. Trinh, Y. Wu, Q. V. Le, H. He, and T. Luong. Solving olympiad geometry without human demonstrations. Nature, 625(7995):476–482, 2024.

[97] A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. Kaiser, and I. Polosukhin. Attention is all you need. In Advances in Neural Information Processing Systems, 2017.

[98] P. Veličković, A. Vitvitskyi, L. Markeeva, B. Ibarz, L. Buesing, M. Balog, and A. Novikov. Amplifying human performance in combinatorial competitive programming. 2024.

[99] A. Verma, L. Pedrosa, M. Korupolu, D. Oppenheimer, E. Tune, and J. Wilkes. Large- scale cluster management at Google with Borg. In Proceedings of the Tenth European Conference on Computer Systems, EuroSys ’15, New York, NY, USA, 2015. Association for Computing Machinery. ISBN 9781450332385. doi: 10.1145/2741948.2741964.

[100] S. Verma, A. Goyal, A. Mathur, A. Anand, and S. Ranu. GRAIL: Graph edit distance and node alignment using llm-generated code. In International Conference on Machine Learning, 2025.

[101] C. Vinuesa del Rio. Generalized Sidon sets. PhD thesis, Universidad Autónoma de Madrid, 2010.

[102] H. Wang, M. Skreta, C. T. Ser, W. Gao, L. Kong, F. Strieth-Kalthof, C. Duan, Y. Zhuang, Y. Yu, Y. Zhu, Y. Du, A. Aspuru-Guzik, K. Neklyudov, and C. Zhang. Efcient evo- lutionary search over chemical space with large language models. In International Conference on Learning Representations, 2025.

[103] Q. Wang, D. Downey, H. Ji, and T. Hope. SciMON: Scientifc inspiration machines optimized for novelty. In Proceedings of the 62nd Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 279–299, Bangkok, Thailand, 2024. Association for Computational Linguistics. doi: 10.18653/v1/2024.acl-long.18.

[104] E. P. White. A new bound for Erdős’ minimum overlap problem. Acta Arithmetica, 208:235–255, 2023.

[105] Q. Wu, G. Bansal, J. Zhang, Y. Wu, B. Li, E. Zhu, L. Jiang, X. Zhang, S. Zhang, J. Liu, A. H. Awadallah, R. W. White, D. Burger, and C. Wang. AutoGen: Enabling next-gen LLM applications via multi-agent conversation. In arXiv preprint arXiv:2308.08155, 2023.

[106] Y. Xia, P. Jin, S. Xie, L. He, C. Cao, R. Luo, G. Liu, Y. Wang, Z. Liu, Y.-J. Chen, Z. Guo, Y. Bai, P. Deng, Y. Min, Z. Lu, H. Hao, H. Yang, J. Li, C. Liu, J. Zhang, J. Zhu, R. Bi, K. Wu, W. Zhang, K. Gao, Q. Pei, Q. Wang, X. Liu, Y. Li, H. Zhu, Y. Lu, M. Ma, Z. Wang, T. Xie, K. Maziarz, M. Segler, Z. Yang, Z. Chen, Y. Shi, S. Zheng, L. Wu, C. Hu, P. Dai, T.-Y. Liu, H. Liu, and T. Qin. Nature language model: Deciphering the language of nature for scientifc discovery. In arXiv preprint arXiv:2502.07527v2, 2025.

[107] K. Yang, A. Swope, A. Gu, R. Chalamala, P. Song, S. Yu, S. Godil, R. J. Prenger, and A. Anandkumar. Leandojo: Theorem proving with retrieval-augmented language models. Advances in Neural Information Processing Systems, 36:21573–21612, 2023.

[108] K. Yang, G. Poesia, J. He, W. Li, K. Lauter, S. Chaudhuri, and D. Song. Formal mathematical reasoning: A new frontier in AI. arXiv preprint arXiv:2412.16075, 2024.

[109] Z. Yang, X. Du, J. Li, J. Zheng, S. Poria, and E. Cambria. Large language models for automated open-domain scientifc hypotheses discovery. In Findings of the Associa- tion for Computational Linguistics: ACL 2024, pages 13545–13565. Association for Computational Linguistics, 2024. doi: 10.18653/v1/2024.findings-acl.804.

[110] Z. Yang, W. Liu, B. Gao, T. Xie, Y. Li, W. Ouyang, S. Poria, E. Cambria, and D. Zhou. MOOSE-Chem: Large language models for rediscovering unseen chemistry scientifc hypotheses. In International Conference on Learning Representations, 2025.

[111] S. Yao, J. Zhao, D. Yu, N. Du, I. Shafran, K. Narasimhan, and Y. Cao. React: Synergizing reasoning and acting in language models. In International Conference on Learning Representations (ICLR), 2023.

[112] S. Yao, F. Liu, X. Lin, Z. Lu, Z. Wang, and Q. Zhang. Multi-objective evolution of heuristic using large language model. In AAAI Conference on Artifcial Intelligence, volume 39, pages 27144–27152, 2025. doi: 10.1609/aaai.v39i25.34922.

[113] G. Ye, X. Cai, H. Lai, X. Wang, J. Huang, L. Wang, W. Liu, and X. Zeng. DrugAssist: A large language model for molecule optimization. In arXiv preprint arXiv:2401.10334, 2023.

[114] H. Ye, J. Wang, Z. Cao, F. Berto, C. Hua, H. Kim, J. Park, and G. Song. ReEvo: Large language models as hyper-heuristics with refective evolution. In Advances in Neural Information Processing Systems, volume 37, 2024.

[115] F. Zhang, S. Nguyen, Y. Mei, and M. Zhang. Genetic Programming for Production Scheduling. Springer, 2021.

[116] H. Zhang, Y. Song, Z. Hou, S. Miret, and B. Liu. HoneyComb: A fexible LLM-based agent system for materials science. In Y. Al-Onaizan, M. Bansal, and Y.-N. Chen, editors, Findings of the Association for Computational Linguistics: EMNLP 2024, pages 3369–3382. Association for Computational Linguistics, Nov. 2024. doi: 10.18653/v1/ 2024.findings-emnlp.192.

[117] Y. Zhou, H. Liu, T. Srivastava, H. Mei, and C. Tan. Hypothesis generation with large language models. In L. Peled-Cohen, N. Calderon, S. Lissak, and R. Reichart, editors, Proceedings of the 1st Workshop on NLP for Science (NLP4Science), pages 117–139. Association for Computational Linguistics, 2024. doi: 10.18653/v1/2024.nlp4scien ce-1.10.

A. 高速行列乗算：完全な結果

結果の全表 表3に、AlphaEvolveによって得られた最高順位を示します。全体として、実験では54種類の行列乗算サイズを検討しました。これらは、\(2 ≤ 𝑚, 𝑛 ≤ 5\) を満たすサイズ \(⟨𝑚, 𝑛, 𝑝⟩\) を大まかに表すように選択され、𝑝については妥当なカットオフが設定されています。基礎となる行列乗算テンソルの対称性により、3つの軸の任意の順列に対して同等のアルゴリズムが存在するため、ソートされたサイズ \(𝑚 ≤ 𝑛 ≤ 𝑝\) に焦点を当てます。

AlphaEvolveは、検討した2つのサイズを除くすべてのサイズにおいて、既知の最高ランクと同等かそれを上回るプログラムを発見しました。ちなみに、問題のサイズを大きくしていくと、いくつかの問題が発生しました。発見したプログラムを、単一のGPUアクセラレータを搭載した評価器で、1000個のランダムシードを用いて⟨5,5,5⟩を超えるサイズで実行すると、メモリ不足に陥ることがよくありました。したがって、より大きな行列サイズにセットアップを拡張するには、さらなる最適化が必要です。

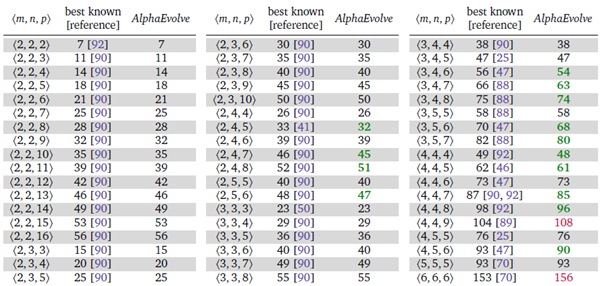
表 3 | 表 2 の完全版。考慮されたすべてのパラメータについて、テンソル分解で AlphaEvolve が得た最高ランクを示しています。54 のターゲットのうち、AlphaEvolve は 38 のケースで最先端技術に匹敵し、14 のケースでそれを上回り (緑)、2 のケースで遅れをとりました (赤)。すべてのケースで、AlphaEvolve は分解に整数または半整数エントリを使用した正確なアルゴリズムを提供します。⟨3,4,7⟩、⟨4,4,4⟩、および ⟨4,4,8⟩ の場合、AlphaEvolve によって発見されたアルゴリズムは複素数値の乗算を使用し、これは複素数値または実数値行列の正確な乗算に使用できます。この表に示されている分解は、付属の Google Colab で見つけることができます。

図 4 (左) の拡大版 図 9a から 9c は、図 4 (左) の拡大版を示しています。これは、2 つの 4 × 4 行列を乗算する演算を表す 3D テンソルのランク 48 の分解を発見するプログラムに対応しています。

図 9a | 図 4 (左) の拡大版。4 × 4 行列を乗算するより高速なアルゴリズムを発見するプログラムを示しています (1/3)。

図 9b | 図 4 (左) の拡大版。4 × 4 行列を乗算するより高速なアルゴリズムを発見するプログラムを示しています (2/3)。

図9c | 図4（左）の拡大版。4×4行列の乗算をより高速に行うアルゴリズムを発見するプログラム（3/3）。ここで、hyperはハイパーパラメータスイープを生成するためのユーザー提供のライブラリです。

B. AlphaEvolveの数学的発見の詳細

このセクションで報告されているすべての構築のデータと検証コードは、付属の Google Colab に掲載されています。

B.1. 最初の自己相関不等式

任意の関数\(f:\mathbb ℝ → \mathbb ℝ\)に対して、\(f\)の自己畳み込みを次のように定義する。 \[ f*f(t) := \int_{\mathbb R} f(t-x)f(x)dx \] \(\mathcal{C}_1\) を次の式を満たす最大の定数とする。 \[ \max_{-1/2\leq t\leq 1/2} f*f(t)\geq \mathcal{C}_1\left(\int_{-1/4}^{1/4} f(x)dx\right)^2 \tag{1} \] 全ての非負\(f:\mathbb ℝ → \mathbb ℝ\)に対して成り立つ。この問題は加法的な組合せ論において、シドン集合の大きさに関連して生じる。現在、 \[ 1.28 ≤ C_1 ≤ 1.5098 \] 下限は[17]で達成され、上限は[68]でステップ関数の構築により達成された。AlphaEvolveは、\([−1/4,1/4]\)上に600個の等間隔区間を持つステップ関数を発見し、わずかに優れた上限\(C_1 ≤ 1.5053\)を与えた。

B.2. 第二自己相関不等式

\(C_2\) を最小の定数とすると、 \[ ∥ f ∗ f ∥_2^2 ≤ C_2∥ f∗f∥_1∥ f∗f∥_∞ \] 全ての非負\(f:\mathbb ℝ → \mathbb ℝ\)に対して、 \[ 0.88922 ≤ C_2 ≤ 1 \] 下限はステップ関数の構築から得られる[68]。AlphaEvolveは、\([−1/4,1/4]\)上に50個の等間隔の区間を持つステップ関数を発見し、わずかに良い下限\(0.8962 ≤ C_2\)を与えた。

B.3. 第三自己相関不等式

\(C_3\)を次の式を満たす最大の定数とする。 \[ \max_{-1/2 \leq t \leq 1/2}| f∗f(t)| ≥ C_3\left(\int_{-1/4}^{1/4}f(x)dx\right)^2 \] 任意の関数 \(f:\mathbb ℝ → \mathbb ℝ\) に対して。\(f\) が正と負の値を取れるようになったので、明らかに \(C_3 ≤ C_1\) である。上限 \(C_3 ≤ 1.45810\) を与えるステップ関数が存在する [101, 75 ページ]。AlphaEvolve は \([−1/4,1/4]\) 上に400 等間隔の区間を持つステップ関数を発見し、これはわずかに良い上限 \(C_3 ≤ 1.4557\) を与える。

B.4. 不確実性不等式

関数\(f:\mathbb ℝ → \mathbb ℝ\)が与えられたとき、フーリエ変換\(\hat{f}(\xi):=\int_{\mathbb ℝ}f(x)e^{−2\pi iz\xi}dx\)を定義し、 \[ A(f):= inf\{r>0:f(x)≥ 0\; for\; all\; |x|≥r \} \] \(C_4\) を最大の定数とすると、 \[ A(f)A(\hat{f}) ≥ C_ 4 \] \(\max(f(0),\hat{f}(0)) < 0\)を満たすすべての偶数\(f\)に対して、 \[ 0.2025 ≤ C_4 ≤ 0.3523. \] （論文では上限は0.353とされていますが、その解を4桁目に丸めると0.3523になります）。我々は[32]と同様の線形結合を用いて、上限を\(C_4 ≤ 0.3521\)に改善しましたが、AlphaEvolveによって発見された定数を使用しました。

\(C_4\) の上限を得るには、条件を満たす特定の「テスト関数」\(f\) を構築し、この関数の値 \(A(f)A(\hat{f})\) を計算します。この値は、上限 \(C_4 ≤ A(f)A(\hat{f})\) を与えます。[32] のアプローチに倣い、テスト関数は \(f(x)=P(x)e^{-\pi x^2}\) の形式で求められます。ここで、\(P(x)\) は、エルミート多項式 \(H_{4k}(x)\) の線形結合として構成される偶多項式です。この形式は、\(H_n(x)e^{-\pi x^2}\) のフーリエ変換が \(i^n H_n(\xi)e^{-\pi \xi^2}\) であるため、特に有用です。偶数多項式 \(P(x)=\sum c_{4k}H_{4k} (x)\) に対して、\(f(x)\) のフーリエ変換は \(\hat{f}(\xi)=\sum c_{4k}i^{4k}H_{4k}(\xi)e^{-\pi \xi^2}=(\sum c_{4k}H_{4k}(\xi))e^{-\pi\xi^ 2}= P(\xi)e^{-\pi \xi^2}\) です。したがって、\(A(f)\) は \(P(x)\) の最大の正の根に関連し、\(A(\hat{f})\) は \(P(\xi)\) の最大の正の根に関連します。具体的には、\(|x| が大きい場合、\(P(x) ≥ 0\) 、A(f)\) は \(P(x)\) の最大の正根となり、\(A(\hat{f})\) は \(P(\xi)\) の最大の正根となり、\(A(f)=A(\hat{f})\) となります。不等式は \(c_4 ≤ (A(f))^2\) となります。

この手法では、多項式 \(P(x) = c_0H_0(x)+c1H_4(x)+c_2H_8(x)+...\) の係数 \(c_0,c_1,c_2,...\) を求めます。この係数は、\(P(x)\) が特定の制約（\(f(0)<0,\hat{f}(0)< 0\) に関連し、大きな \(|x|\) に対して正であること）を満たし、\(P(x)\) の最大の正の根を最小化します。このアプローチでは、多項式 \(P(x)\) は \(P(0) = 0\)（最適化プロセスで制約を簡素化するために使用される条件）となるように構築されます。つまり、\(P(x)\) の係数は \(x^2\) になります。 \(P(x)\) の最大の正根 \(r_{max}\) は、\(P(x)/x^2\) の最大の正根である。この構成から導かれる \(C_4\) の上限は \(r_{max}^2/(2\pi)\) である。

AlphaEvolveによって発見された\(P(x)=c_0H_0(x)+c_1H_4(x)+c_2H_8(x)\)の定数は、\([c_0,c_1,c_2] ≈ [0.32925,−0.01159,−8.9216 × 10^{-5}]\)です。これらの係数を用いて\(P(x)\)を構築し、その最大の正の根\(r_{max}\)（\(P(x)/x^2\)の最大の正の根を求めることによって）を求め、\(r_{max}^2/(2\pi)\)を計算すると、改善された上限\(C_4 ≤ 0.3521\)が得られます。定性的に我々の線形結合は[32]で見つかったものと非常に類似しており、したがって彼らの仮説を経験的に確認し、その構築はほぼ最適であることを示しています。

B.5. エルデシュの最小重複問題

\(C_5\) を最大の定数とすると、 \[ \sup_{x\in [-2,2]} \int_{-1}^1 f(t)g(x+t)\; dt\geq C_5 \]

図 10 | エルデシュの最小重なり問題に対して AlphaEvolve によって発見された構成。

\(f,g: [−1,1] → [0,1]\) に対して、\([−1,1]\) 上および \(\int f = 1\) 上で \(f+g = 1\) となる定数である。ただし、\([−1,1]\) の外側では \(f,g\) をゼロで拡張する。この定数は [24] の最小重複問題の漸近挙動を制御する。 \[ 0.379005 ≤ C_5 ≤ 0.380927 \] は既知であり、下限値は[104]で凸計画法によって得られたものである。

この定数は、\([0,1]\)に値を持ち、\(\int_0^2 ℎ(x)dx = 1\)を満たす\([0,2]\)上のすべてのステップ関数\(h\)の下限値に等しいことが知られている（[39]を参照）。 \[ \max_{k} \int h(x)(1-h(x+k))dx \] この結果を用いて、[39]ではステップ関数の構築によってエルデシュ最小重なり問題の上限が得られた。図10に示すステップ関数は、以前の上限よりもわずかに良い値を示し、上限は\(C_5 ≤ 0.380924\)となる。

B.6. 有限集合の和と差

\(C_6\) を次の命題が成り立つ最大の定数とします。\(|A+B|≪ |A|\) かつ \(|A−B|≫ |A+B|^{C_6}\) を満たす任意の大きさの有限整数集合 \(A,B\) が存在する。(ここで \(A+B=\{a+b:a∈A ,b∈B\}\) および \(A−B=\{a−b:a∈A ,b∈B\}\) はそれぞれ和集合および差集合を表す。\(X≪Y\) という表記は、\(A, B\) から独立な定数 \(C\) に対して \(X ≤ CY\) であることを意味する(十分に大きい集合 \(A,B\) に対して)。\(X≫Y\) という表記は、\(X≥C^\prime Y\) であることを意味する。 \(C^\prime\) は集合 \(A,B\) とは独立である（十分に大きな集合 \(A,B\) の場合）。 \[ 1.14465 ≤ C_6 ≤ \frac{4}{3} \tag{2} \] 上限については[38, 系3]を、下限については[38, 定理1]を参照。下限値を求める主なツールは、Gyarmati et al. [38]による以下の結果である。 \[ C_6 \geq 1 + \frac{\log\frac{|U-U|}{|U+U|}}{\log(2\max(U)+1)} \tag{3} \] 0を含み、\(|U−U| ≤ 2max(U)+1\)を満たす任意の非負整数の有限集合\(U\)について。AlphaEvolveは、下限を\(1.1479 ≤ C_6\)まで改善するサイズ2003の集合\(U_1\)を発見し、さらに下限を\(1.1584 ≤ C_6\)まで改善するサイズ54265の集合\(U_2\)を発見した。

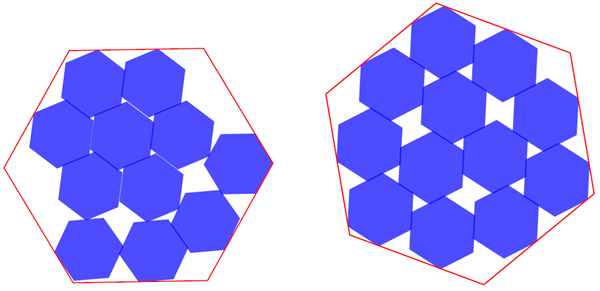
図11 | AlphaEvolveによって発見されたパッキング問題の構成。左：辺の長さが3.931の正六角形に11個の単位六角形をパッキングする。右：辺の長さが3.942の正六角形に12個の単位六角形をパッキングする。

B.7. 正六角形の中に単位正六角形を詰め込む

単位辺長を持つ \(n\) 個の互いに素な正六角形を、より大きな正六角形に詰め込み、外側の六角形の辺長を最小化する問題を考えてみましょう。\(n\)= 11 および \(\n\)= 12 の場合、最もよく知られている構成では、外側の六角形の辺長はそれぞれ 3.943 および 4.0 です [28]。AlphaEvolve は、これらの境界をそれぞれ 3.931 および 3.942 に改善する詰め込み配置を発見しました。これらの配置を図 11 に示します。

B.8. 最大距離と最小距離の比を最小化する

この問題の目的は、任意の \(n\) と \(d\) に対して、\(d\) 次元空間において、最大と最小のペア間距離の比を最小化する \(n\) 点を見つけることです。AlphaEvolve は、既知の最良の境界値を改善する 2 つの新しい構成を発見しました。発見された構成を図 12 に示します。

2次元では、AlphaEvolveは比\(≈ \sqrt{12.889266112}\)を持つ点を16個発見し、既知の最高値12.890[28]を改善しました。（この参考文献では、比そのものではなく、比の2乗が報告されており、私たちも同じ表記法を使用しています。）

3次元では、AlphaEvolveは比率\(≈ \sqrt{4.165849767}\)を持つ14個の点を発見し、既知の最高境界4.168[28]を改善しました。

B.9. 三角形のハイルブロン問題

この問題の目的は、単位面積の三角形上または内部の点を探し、それらの点によって形成される最小の三角形の面積が最大となるようにすることです。= 11の場合、SOTAは0.036でした[28]。AlphaEvolveは、図13（左）に示すように、最小面積が0.0365より大きい構成を発見しました。

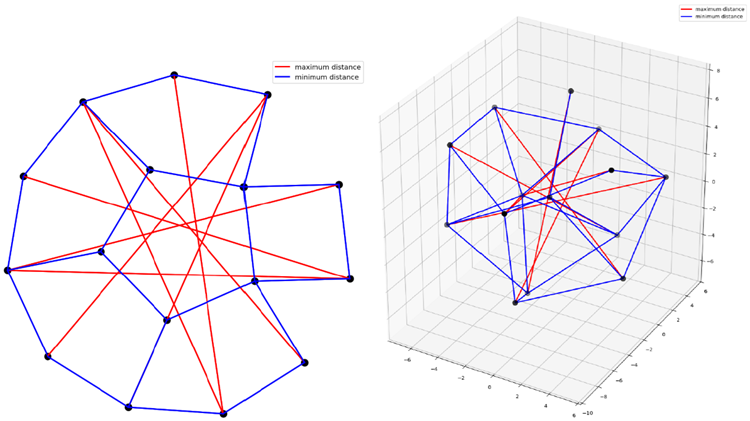
図12 | 左：2次元で最大距離と最小距離の比が \(≈ \sqrt{12.889266112}\) となる16点。右：3次元で最大距離と最小距離の比が \(≈ \sqrt{4.165849767}\) となる14点。どちらの構成も、既知の最良の境界値を改善している。

B.10. 凸領域におけるハイルブロン問題

この問題の目的は、単位面積の凸領域上または内部の点を探し、それらの点によって形成される最小の三角形の面積が最大になるようにすることです。AlphaEvolveは、最もよく知られている2つの境界を改善しました。

𝑛 = 13の場合、SOTAは0.0306 [28]でしたが、AlphaEvolveによって0.0309に改善されました（図13（中央）参照）。𝑛 = 14の場合、SOTAは0.0277 [28]でしたが、AlphaEvolveによって0.0278に改善されました（図13（右）参照）。

B.11. 11次元におけるキス数

キッシング問題とは、与えられた単位球に接して、互いに素な単位球をいくつ詰め込めるかという問題である。次元におけるそのような最大数は、次元キッシング数と呼ばれる [8]。 = 11 の場合、最もよく知られている下限は 592 [30] で、AlphaEvolve はこれを 593 に改良した。次元 11 におけるキッシング数の下限 593 を証明するために、AlphaEvolve は、(a) これらの点の最大ノルムがそれらの最小ペアワイズ距離よりも小さく、(b) 任意の点のペアについて、それらのドット積の平方根がそれらの両方のノルムよりも小さい、という条件を満たす 11 次元の点を 593 個見つけた。が見つかった点の最大ノルムを表すものとし、すべての点を正規化して、それらのノルムがに等しくなるようにする。2 番目の特性のため、この正規化によってそれらの最小ペアワイズ距離は減少しない。したがって、ノルムを 2 に縮小し、ポイントを中心とした単位球をパックすると、593 ポイントの有効なキス構成が得られます。

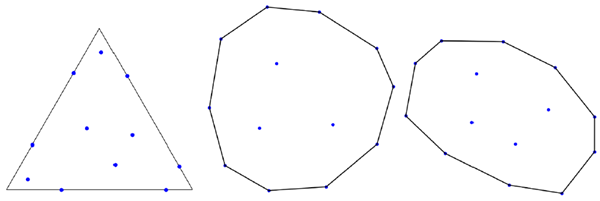
図13 | AlphaEvolveによって発見された、ハイルブロン問題の2つの変種における既知の最良の境界を改善する新たな構成。左：単位面積三角形内の11点。形成された三角形の面積はすべて0.0365以上。中央：単位面積の凸領域内の13点。形成された三角形の面積はすべて0.0309以上。右：最小面積が0.0278以上の単位凸領域内の14点。

B.12. 単位正方形内に円を詰め込み、半径の合計を最大化する

正の整数が与えられたとき、問題は単位正方形の中に互いに隣接しない円を詰め込み、それらの半径の合計が最大になるようにすることです。AlphaEvolveは、従来の技術を改善する2つの新しい構成を発見しました[28]。

𝑛 = 26 の場合、SOTA は 2.634 でしたが、AlphaEvolve によって 2.635 に改善されました。図 14 (左) を参照してください。𝑛 = 32 の場合、SOTA は 2.936 でしたが、AlphaEvolve によって 2.937 に改善されました。図 14 (中央) を参照してください。

B.13. 周囲長4の長方形内に円を詰め込み、半径の合計を最大化する

正の整数𝑛が与えられたとき、問題は周囲長4の長方形内に𝑛個の互いに交わらない円を詰め込み、それらの半径の合計が最大になるようにすることです。AlphaEvolveは𝑛 = 21に対して新しい構成を発見し、従来の解を2.364 [28] から2.3658に改善しました。図14（右）を参照してください。

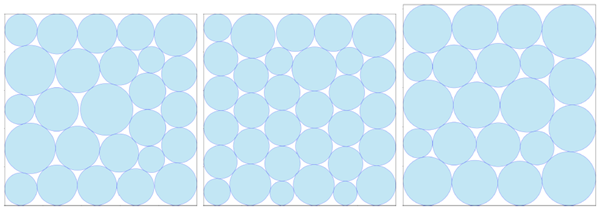
図14 | AlphaEvolveによって発見された、半径の合計を最大化する円の詰め込みに関する既知の最良の境界を改良した新しい構成。左：単位正方形内に半径の合計が\(2.635 ≥ )である26個の円。中央：単位正方形内に半径の合計が\(2.937 ≥ )である32個の円。右：周囲長4の長方形内に半径の合計が\(2.365 ≥ )である21個の円。

AlphaEvolve: A coding agent for scientifc and algorithmic discovery